
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нижняя и верхняя цены игры в смешанных стратегиях.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Игру, определяемую матрицей А, имеющей m строк и n столбцов, называют конечной игрой размерности mxn. Пусть игрок А выбирает некоторую стратегию Аi, тогда в наихудшем случае он получит выигрыш, равный Величина Стратегия, обеспечивающая получение Игрок В, выбирая стратегию, исходит из следующего принципа: при выборе некоторой стратегии Вj его проигрыш не превосходит максимального из значений элементов j-го столбца матрицы, т.е. меньше или равен Величина Нижняя цена игры всегда не превосходит верхней цены игры. Если Для игры с седловой точкой нахождение решения состоит в выборе максиминной и минимаксной стратегий, которые являются оптимальными. Седловая точка Доказательство теоремы о существовании в любой конечной матричной игре нижней и верхней цен игры в смешанных стратегиях. Так как функция α (P) по лемме H (P,Q): где P= Аналогичным образом обосновывается существование верхней цены игры в смешанных стратегиях
27. Понятие стратегии, оптимальной во множестве смешанных стратегий. Основная теорема матричных игр Дж.Фон Неймана. • игра без седловой точки; • игроки используют случайную смесь чистых стратегий с заданными вероятностями; • игра многократно повторяется в сходных условиях; • при каждом из ходов ни один игрок не информирован о выборе стратегии другим игроком; • допускается осреднение результатов игр. 2) Для матричной игры с любой матрицей А величины
Доказательство критерия оптимальности смешанной стратегии игрока А в терминах задаваемых цены игры в смешанных стратегиях, выигрыш-функции в смешанных стратегиях и множества смешанных стратегий игрока В. В определении равновесной ситуации в чистых стратегиях ( max (1≤i≤m)F(
29. Доказательство критерия оптимальности смешанной стратегии игрока Теорема. Для того, чтобы стратегия Qo игрока В была оптимальной, необходимо и достаточно, чтобы выполнялось неравенство H(P,Qo)≤V для любого РϵSB, т.е. выбор игроком В одной из своих оптимальных стратегий Qo гарантирует ему проигрыш, не большей цены игры V, при любой стратегии Р игрока А. Доказательство. Пусть Qo – оптимальная стратегия игрока В. Тогда по основной теореме матричных игр фон Неймана показатель эффективности β(Qo) стратегии Qo равен цене игры V: V= β(Qo). Рассматривая β(Qo) как показатель эффективности β(Qo, SA) стратегии Qo относительно множества SA смешанных стратегий игрока А, будем иметь по определению β(Qo, SA)=maxH(P,Qo). Следовательно, V= β(Qo)= β(Qo, SA)=maxH(P,Qo), откуда получаем неравенство H(P,Qo)≤V. Но V= V¾=min β(Q)≤ β(Qo). Получаем β(Qo)=V, которое в силу теоремы фон Неймана означает, что стратегия Qo являеься оптимальной. 30. Доказательство критерия оптимальности смешанной стратегии игрока Теорема. Пусть V- цена игра, H(P0,Q) – функция выигрыша, SCB={B1,…,Bn} – множество чистых стратегий игрока В. Для того чтобы стратегия Р0 игрока А была оптимальной, необходимо и достаточно, чтобы Н(Р0,Bj)≥V, j=1,…,n. Доказательство. Достаточно установить эквивалентность неравенств H(P0, Q)≥V и Н(Р0,Bj)≥V. Докажем эквивалентность. Пусть справедливо неравенство H(P0, Q)≥V. Так как это неравенство имеет место для любой стратегии QϵSB игрока В, то оно, в частности, будет справедливым и для его чистых стратегий Bjϵ SCB, j=1,…,n, т.е. неравенство Н(Р0,Bj)≥V имеет место. Таким образом импликация H(P0, Q)≥V на Н(Р0,Bj)≥V доказана. Теперь пусть имеет место неравенство Н(Р0,Bj)≥V, j=1,…,n. Тогда по формуле Н(Р0,Bj)≥V на H(P0, Q)≥V и, следовательно, эквивалентность H(P0, Q)≥V и Н(Р0,Bj)≥V.
31. Доказательство критерия оптимальности смешанной стратегии игрока Теорема. Пусть V- цена игра, H(P,Q0) – функция выигрыша, SCA={A1,…,An} – множество чистых стратегий игрока A. Для того чтобы стратегия Q0 игрока В была оптимальной, необходимо и достаточно, чтобы Н(Ai,Q0)≤V, i=1,…,n. Доказательство. Достаточно установить эквивалентность неравенств H(P,Qo)≤V и Н(Ai,Q0)≤V. Докажем эквивалентность. Пусть справедливо неравенство H(P,Qo)≤V. Так как это неравенство имеет место для любой стратегии PϵSA игрока A, то оно, в частности, будет справедливым и для его чистых стратегий Aiϵ SCA, i=1,…,n, т.е. неравенство H(P,Qo)≤V имеет место. Таким образом импликация H(P,Qo)≤V на Н(Ai,Q0)≤V доказана. Теперь пусть имеет место неравенство Н(Ai,Q0)≤V, i=1,…,n. Тогда по формуле Н(Ai,Q0)≤V на H(P,Qo)≤V и, следовательно, эквивалентность H(P,Qo)≤V и Н(Ai,Q0)≤V.
32. Доказательство теоремы о геометрической интерпретации множества стратегий игрока Следствие. Множество SOA оптимальных стратегий игрока А является выпуклым многогранником (политопом), содержащимся в симплексе SA всех смешанных стратегий игрока А. Доказательство. Для каждой оптимальной стратегии Р0=(р01,…,р0m) игрока А справедливо неравенство Н(Р0,Bj)≥V, j=1,…,n, которое можно переписать следующим образом:
33. Доказательство теоремы о геометрической интерпретации множества стратегий игрока Следствие. Множество SOВ оптимальных стратегий игрока В является выпуклым многогранником (политопом), содержащимся в симплексе SВ всех смешанных стратегий игрока В. Доказательство. Для каждой оптимальной стратегии Q0=(q01,…,q0m) игрока А справедливо неравенство Н(Ai,Q0)≤V, i=1,…,m, которое можно переписать следующим образом:
34. Доказательство в терминах множеств смешанных стратегий игроков Теорема. Для того чтобы V было ценой игры, а Р0 и Q0 – оптимальными стратегиями соответственно игроков А и В, другими словами, для того, чтобы {P0,Q0,V} было решеннием игры, необходимо и достаточно выполнение двойного неравенства H(P,Q0)≤V≤H(P0,Q) для любых PϵSA и QϵSB. Доказательство. Необходимость. Пусть V – цена игры и P0, Q0 – оптимальные стратегии. Тогда неравенства H(P,Qo)≤V и H(P0, Q)≥V справедливы и их можно записать в неравенство H(P,Q0)≤V≤H(P0,Q). Достаточность. Пусть для некоторого числа V и некоторых стратегий Р0 игрока А и Q0 игрока В выполняется двойное неравенство (P,Q0)≤V≤H(P0,Q). Так как это неравенство верно для любых PϵSA и QϵSB, то в частности оно будет справедливо и для Р= P0, Q= Q0: H(P0,Q0)≤V≤H(P0,Q0), т.е. V=H(P0,Q0). Тогда получим: H(P,Q0)≤ H(P0,Q0)≤H(P0,Q), PϵSA и QϵSB. max(PϵSA)H(P,Q0)≤ H(P0,Q0)≤min(QϵSB)H(P0,Q) или β(Qo)≤ H(P0,Q0)≤α(Р0). Отсюда по определению верхней и нижней цен игры получим: V¾=min(QϵSB)β(Q)≤ β(Qo)≤ H(P0,Q0)≤α(Р0)≤ max(PϵSA) α(Р)=V¾. Из H(P0,Q0)≤V≤H(P0,Q0) и V¾=min(QϵSB)β(Q)≤ β(Qo)≤ H(P0,Q0)≤α(Р0)≤ max(PϵSA) α(Р)=V¾. следует, что V – цена игры, а также справедливость равенства V= α(Р0)= β(Qo)= H(P0,Q0), которое по определению оптимальных стратегий, означает, что P0,Q0 – оптимальные стратегии соответственно игроков А и В.
35. Доказательство в терминах множеств чистых стратегий игроков Теорема. Для того, чтобы V была ценой игры, а P0,Q0 – оптимальными стратегиями соответственно игроков А и В, необходимо и достаточно выполнение двойного неравенства Н(Ai,Q0)≤V≤ Н(Р0,Bj), i=1,…,m, j=1,…,n. Доказательство. Достаточно доказать эквивалентность неравенств H(P,Q0)≤V≤H(P0,Q) и Н(Ai,Q0)≤V≤ Н(Р0,Bj). Пусть справедливо неравенство H(P,Q0)≤V≤H(P0,Q). Так как оно имеет место для любых стратегий PϵSA и QϵSB, то, в частности, оно справедливо и для любых чистых стратегий P=Ai, i=1,…,m, и Q=Bj, j=1,…,n, т.е. справедливо двойное неравенство Н(Ai,Q0)≤V≤ Н(Р0,Bj). Докажем обратное. Пусть имеет равенство Н(Ai,Q0)≤V≤ Н(Р0,Bj). Тогда из него, допустив получим:
36. Доказательство в терминах седловых точек выигрыш-функции критерия того, что число - цена игры в смешанных стратегиях, а PO и QO - стратегии, оптимальные во множестве смешанных стратегий соответственно игроков А и B. Для того чтобы V было ценой игры, а Р° и Qo — оптимальными стратегиями соответственно игроков А и В, необходимо и достаточно, чтобы (Р°, Q°) была седловой точкой выигрыш-функции Н(Р, Q) и Н(Р°, Q°) = V. Множество номеров i ∈ {1,2,…,m}, для которых pi> 0, называется спектром смешанной стратегии Р={р1,р2,…, рm) и обозначается supp Р. Таким образом, suppР = {i∈{1,2,..., m):рi>0} Чистая стратегия Ai- называется пассивной или активной относительно смешанной оптимальной стратегии Р° = (р1O,р2O,..., рmO)в зависимости от того, i не ∈supp Р° или i∈supp Р°, т.е. в зависимости от того, pi0 = 0 или рi0> 0.
|
||
|
Последнее изменение этой страницы: 2017-01-27; просмотров: 1797; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

 . Предвидя такую возможность, игрок А должен выбирать такую стратегию, чтобы максимизировать свой минимальный выигрыш
. Предвидя такую возможность, игрок А должен выбирать такую стратегию, чтобы максимизировать свой минимальный выигрыш  :
:
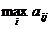 . Поэтому игрок В, очевидно, выберет такое значение j, при котором его максимальный проигрыш
. Поэтому игрок В, очевидно, выберет такое значение j, при котором его максимальный проигрыш  минимизируется:
минимизируется:
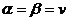 , то число v называется ценой игры. Игра, для которой
, то число v называется ценой игры. Игра, для которой  , называется игрой с седловой точкой.
, называется игрой с седловой точкой. соответствует оптимальным стратегиям игроков
соответствует оптимальным стратегиям игроков  .
.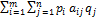 (P,Q)Î
(P,Q)Î 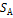 x
x 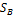 ,
, , Q=(
, Q=( ) непрерывна на компакте
) непрерывна на компакте  =max(PÎ
=max(PÎ 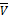 =min(QÎ
=min(QÎ 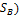 β(Q)
β(Q)
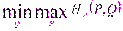
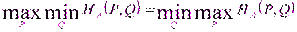

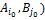 , учитывая, что(
, учитывая, что(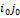 , гдеF – функция выигрыша, неравенство можно переписать в виде неравенства
, гдеF – функция выигрыша, неравенство можно переписать в виде неравенства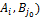 =F(
=F(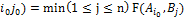 которое соответствует неравенству, а равенство в виде равенства соответствующего равенству. Это означает по данному определению седловой точки функции, что равновесная ситуация в чистых стратегиях (
которое соответствует неравенству, а равенство в виде равенства соответствующего равенству. Это означает по данному определению седловой точки функции, что равновесная ситуация в чистых стратегиях (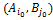 =a
=a 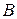 в терминах задаваемых цены игры в смешанных стратегиях, выигрыш-функции в смешанных стратегиях и множества смешанных стратегий игрока А.
в терминах задаваемых цены игры в смешанных стратегиях, выигрыш-функции в смешанных стратегиях и множества смешанных стратегий игрока А.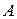 в терминах задаваемых цены игры в смешанных стратегиях, выигрыш-функции в смешанных стратегиях и множества чистых стратегий игрока
в терминах задаваемых цены игры в смешанных стратегиях, выигрыш-функции в смешанных стратегиях и множества чистых стратегий игрока 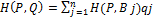 с учетом того, что
с учетом того, что  =1, получим,
=1, получим, 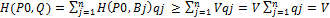 , QϵSB, т.е. доказано неравенство H(P0, Q)≥V. Таким образом, справедлива импликация
, QϵSB, т.е. доказано неравенство H(P0, Q)≥V. Таким образом, справедлива импликация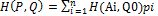 с учетом того, что
с учетом того, что 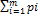 =1, получим,
=1, получим,  , PϵSA, т.е. доказано неравенство H(P,Qo)≤V. Таким образом, справедлива импликация
, PϵSA, т.е. доказано неравенство H(P,Qo)≤V. Таким образом, справедлива импликация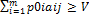 , j=1,…,n. Множество точек Р0=(р01,…,р0m) m-мерного пространства Rm, координаты p0i, i=1,…,m, которых удовлетворяет этому неравенству для фиксированного jϵ{1,…,n}, является замкнутым полупростанством, а множество точек Р0=(р01,…,p0m), координаты p0i, i=1,…,m, которых удовлетворяют этому неравенству для всех j=1,…,n, является пересечением конечного числа n замкнутых полупростанств и называется выпуклым замкнутым полиэдром. Так как к тому же множество оптимальных оптимальных стратегий игрока А SOA ограничено, поскольку оно является подмножеством симплекса всех его смешанных стратегий SA, то SOA является выпуклым многогранником.
, j=1,…,n. Множество точек Р0=(р01,…,р0m) m-мерного пространства Rm, координаты p0i, i=1,…,m, которых удовлетворяет этому неравенству для фиксированного jϵ{1,…,n}, является замкнутым полупростанством, а множество точек Р0=(р01,…,p0m), координаты p0i, i=1,…,m, которых удовлетворяют этому неравенству для всех j=1,…,n, является пересечением конечного числа n замкнутых полупростанств и называется выпуклым замкнутым полиэдром. Так как к тому же множество оптимальных оптимальных стратегий игрока А SOA ограничено, поскольку оно является подмножеством симплекса всех его смешанных стратегий SA, то SOA является выпуклым многогранником. , j=1,…,m. Множество точек Q0=(q01,…,q0m) m-мерного пространства Rm, координаты q0i, i=1,…,m, которых удовлетворяет этому неравенству для фиксированного jϵ{1,…,n}, является замкнутым полупростанством, а множество точек Q0=(q01,…,q0m), координаты q0i, i=1,…,m, которых удовлетворяют этому неравенству для всех j=1,…,n, является пересечением конечного числа n замкнутых полупростанств и называется выпуклым замкнутым полиэдром. Так как к тому же множество оптимальных оптимальных стратегий игрока B SOB ограничено, поскольку оно является подмножеством симплекса всех его смешанных стратегий SB, то SOB является выпуклым многогранником.
, j=1,…,m. Множество точек Q0=(q01,…,q0m) m-мерного пространства Rm, координаты q0i, i=1,…,m, которых удовлетворяет этому неравенству для фиксированного jϵ{1,…,n}, является замкнутым полупростанством, а множество точек Q0=(q01,…,q0m), координаты q0i, i=1,…,m, которых удовлетворяют этому неравенству для всех j=1,…,n, является пересечением конечного числа n замкнутых полупростанств и называется выпуклым замкнутым полиэдром. Так как к тому же множество оптимальных оптимальных стратегий игрока B SOB ограничено, поскольку оно является подмножеством симплекса всех его смешанных стратегий SB, то SOB является выпуклым многогранником.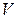 - цена игры в смешанных стратегиях, а
- цена игры в смешанных стратегиях, а 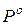 и
и 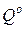 - стратегии, оптимальные во множестве смешанных стратегий соответственно игроков
- стратегии, оптимальные во множестве смешанных стратегий соответственно игроков 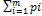 =
= 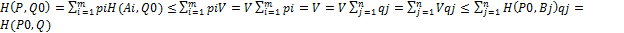 , PϵSA и QϵSB, т.е. справедливо неравенство H(P,Q0)≤V≤H(P0,Q).
, PϵSA и QϵSB, т.е. справедливо неравенство H(P,Q0)≤V≤H(P0,Q).


