
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели эффективности чистых стратегий. Максиминные и минимаксные стратегии.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим матричную m × n - игру с игроками А и В,в которой игрок А обладает mчистыми стратегиями
аi 1, аi 2, …, аin, расположенных в i -й строке матрицы, в зависимости от выбранной игроком В стратегии. Предполагая поведение игрока А крайне осмотрительным, необходимо считать, что игрок В сыграет наилучшим для себя образом и на выбор игроком А стратегии Аi выберет ту стратегию Bj, при которой выигрыш игрока А окажется минимальным. Обозначим минимальный среди выигрышей через α i:
и назовем его показателем эффективности стратегии Аi. Продолжая действовать разумно, игрок А должен выбрать ту стратегию, которая максимизирует показатель эффективности, т.е. для которой число α i максимально. Если обозначить это максимальное число через α:
тогда
Описанный принцип выбора эффективной стратегии игроком А называется максиминным принципом, а выигрыш α - максимином. Стратегия называется максиминной стратегией игрока А. Пусть игрок А выбрал максиминную стратегию
Данное неравенство означает, что если игрок А в игре будет следовать максиминной стратегии, то ему при любой игре противника В гарантирован выигрыш в чистых стратегиях, не меньший максимина α. Именно поэтому максимин α, определяемый по формуле Теперь рассмотрим игру с точки зрения игрока В, который стремится минимизировать выигрыш игрока А, исходя из посылки, что игрок А играет наилучшим для себя и наихудшим для игрока В образом. Если игрок В выберет стратегию а 1 j, а 2 j, …, аmj,
выигрышей, стоящих в j -м столбце игровой матрицы, в зависимости от того, какой стратегии будет придерживаться игрок А. Но так как игрок В предполагает, что игрок А играет наилучшим для себя образом, то выигрышем игрока А будет максимальное из чисел а 1 j, а 2 j, …, аmj; обозначим его через βj:
и назовем показателем неэффективности стратегии Вj. Таким образом, для любой стратегии Bj игрока В наибольший его проигрыш равен β j. В интересах игрока В - выбрать стратегию с минимальным показателем неэффективности. Наименьшее из чисел обозначим β:
Отсюда в силу формулы
Выбор игроком В стратегии с наименьшим показателем β j оправдывает то, что он назван показателем неэффективности. Критерий выбора эффективной стратегии для игрока В называется минимаксным принципом, а выигрыш β называется минимаксом. Стратегия
называется минимаксной стратегией игрока В. При выборе игроком В стратегии bj1 = -a1j, bj2 = -a2j,..., bjm = -amj. Тогда показателем эффективности стратегии Bj (относительно выигрышей игрока В) будет минимальное из этих чисел, которое, в силу обозначения
а максимином будет число
Таким образом, показатель эффективности стратегии Bj (относительно выигрышей игрока B) противоположен показателю неэффективности стратегии Bj (относительно проигрышей игрока В) и максимин (относительно выигрышей игрока В) противоположен минимаксу (относительно проигрышей игрока B).
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-27; просмотров: 553; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.42.41 (0.021 с.) |

 ={А1,..., Аm}, a игрок В - n чистыми стратегиями
={А1,..., Аm}, a игрок В - n чистыми стратегиями 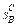 ={В1,..., Вn}. Значения функции выигрыша игрока A обозначим через аij,т. е. FA (i, j) = аij, и тогда матрица игры будет иметь вид
={В1,..., Вn}. Значения функции выигрыша игрока A обозначим через аij,т. е. FA (i, j) = аij, и тогда матрица игры будет иметь вид

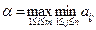
 соответствующая максимину α, т. е. стратегия
соответствующая максимину α, т. е. стратегия  номер i 0 которой максимизирует показатель эффективности α i, т. е.
номер i 0 которой максимизирует показатель эффективности α i, т. е. 
 а игрок В - какую-то произвольную стратегию Bj, j = 1,..., п. Тогда в создавшейся ситуации (
а игрок В - какую-то произвольную стратегию Bj, j = 1,..., п. Тогда в создавшейся ситуации ( для которого в силу равенств
для которого в силу равенств 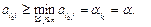
 , то выигрышем игрока А может быть один из
, то выигрышем игрока А может быть один из


 для которой
для которой
 , его проигрышем может быть один из проигрышей а 1 j, а 2 j, …, аmj, или, другими словами, его выигрышем может быть один из выигрышей
, его проигрышем может быть один из проигрышей а 1 j, а 2 j, …, аmj, или, другими словами, его выигрышем может быть один из выигрышей
 выражающееся иначе следующим образом:
выражающееся иначе следующим образом:



