
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналитическое решение игры без седловой точки, задаваемой симметрической и двоякосимметрической матрицей второго порядка.Содержание книги
Поиск на нашем сайте
Если матрица игры А размером 2x2 симметрическая, т. е.
Если матрица игры А размера 2x2 двоякосимметрическая, т. е.
8. Геометрический метод нахождения оптимальных смешанных стратегий игрока 1. Берем горизонтальный отрезок [0, 1], на котором для определенности положено а 22 < а 11 < а 21 < а 12.
2. В концах отрезка [0, 1] проводим к нему два перпендикуляра: левый, соответствующий стратегии А1 и правый, соответствующий стратегии А2. 3. На левом перпендикуляре от точки 0 его пересечения с отрезком [0, 1] откладываем (как на вертикальной числовой оси) элементы а 11 и а 12первой строки матрицы А. 4. На правом перпендикуляре от точки 1 его пересечения с отрезком [0, 1] откладываем (как на вертикальной числовой оси) элементы а 21 и а 22второй строки матрицы А. 5. Соединяем точки, изображающие элементы с одинаковыми вторыми индексами, т.е. элементы, стоящие в одном и том же столбце матрицы А: а 11 с а 21и а 12 с а 22. В результате получаем отрезки а 11 а 21и а 12 а 22.
Если отрезки а 11 а 21и а 12 а 22 возрастающие: а 11 а 21и а 12 а 22 , то стратегия А 2 строго доминирует стратегию А 1. 7. Если отрезок а 11 а 21 лежит не ниже отрезка а 12 а 22, то стратегия В 2 доминирует стратегию В 1. Если отрезок а 11 а 21 лежит выше отрезка а 12 а 22и не пересекается с ним, то стратегия В 2строго доминирует стратегию В 1. 8. Находим нижнюю огибающую отрезков а 11 а 21и а 12 а 22. 9. Находим наивысшие точки нижней огибающей. 10. Проектируем их ортогонально на горизонтальный отрезок [0,1]. 11. Полученные проекции р° определяют оптимальные стратегии Р°=(1-р°, р°) игрока А. 12. Ордината наивысшей точки огибающей равна пене игры V. 13. Верхний из двух концов нижней огибающей (лежащих на перпендикулярах) есть нижняя цена игры в чистых стратегиях a. 14. Нижний из двух верхних концов отрезков а 11 а 21и а 12 а 22 есть верхняя цена игры в чистых стратегиях b. 15. Если элемент является нижним на перпендикуляре, где он лежит, и верхним концом отрезка а 11 а 21или а 12 а 22., на котором он лежит, то этот элемент является седловой точкой. В этом случае чистая стратегия игрока В, номер которой совпадает со вторым индексом седло-вой точки, является оптимальной. 9. Геометрический метод нахождения оптимальных смешанных стратегий игрока
1. Берем горизонтальный отрезок [0, 1], на котором для определенности положено а 22 < а 11 < а 21 < а 12
2. В концах отрезка [0, 1] проводим к нему два перпендикуляра: левый, соответствующий стратегии В 1и правый, соответствующий стратегии В 2, 3. На левом перпендикуляре от точки 0 его пересечения с отрезком [0, 1] откладываем (как на вертикальной числовой оси) элементы а 11 и а 21первого столбца матрицы А. 4. На правом перпендикуляре от точки 1 его пересечения с отрезком [0, 1] откладываем (как на вертикальной числовой оси) элементы а 12 и а 22второго столбца матрицы А. 5. Соединяем точки, изображающие элементы с одинаковыми первыми индексами, т.е. элементы, стоящие в одной и той же строке матрицы А: а 11 с а 12и а 21 с а 22. В результате получаем отрезки а 11 а 12и а 21 а 22
Если отрезки а 11 а 12и а 21 а 22 убывающие: а 11 а 12 ¯ и а 21 а 22 ¯, то стратегия В 2строго доминирует стратегию В 1. 7. Если отрезок а 11 а 12лежит не ниже отрезка а 21 а 22 то стратегия А 1 доминирует стратегию А 2. Если отрезок а 11 а 12лежит выше отрезка а 21 а 22 и не пересекается с ним, то стратегия А 1строго доминирует стратегию А 2. 8. Находим верхнюю огибающую отрезков а 11 а 12и а 21 а 22. 9. Находим наинизщие точки верхней огибающей. 10. Проектируем их ортогонально на горизонтальный отрезок [0, 1]. 11. Полученные проекции q° определяют оптимальные стратегии Q°= (1-q0,q°) игрока В. 12. Ордината наинизшей точки верхней огибающей равна цене игры V. 13. Нижний из двух концов верхней огибающей (лежащих на перпендикулярах) есть верхняя цена игры в чистых стратегиях b. 14. Верхний из двух нижних концов отрезков а 11 а 12и а 21 а 22 есть нижняя цена игры в чистых стратегиях a. 15. Если элемент является верхним на перпендикуляре, где он лежит, и нижним концом отрезка а 11 а 12или а 21 а 22, на котором он лежит, то этот элемент является седловой точкой. В этом случае чистая стратегия игрока А, номер которой совпадает с первым индексом седловой точки, является оптимальной.
10. Геометрический метод нахождения оптимальных смешанных стратегий игрока
1. Берем горизонтальный отрезок [0, 1]. 2. Через концы отрезка [0,1] проводим к нему два перпендикуляра: левый и правый. 3. На левом перпендикуляре от точки 0 его пересечения с отрезком [0, 1] откладываем (как на вертикальной числовой оси) все элементы первой строки матрицы А. 4. На правом перпендикуляре от точки 1 его пересечения с отрезком [0, 1] откладываем (как на вертикальной числовой оси) все элементы второй строки матрицы А. 5. Каждую пару точек, изображающих элементы а 1j и a 2j, j=1,2,..., п, стоящие j-м столбце матрицы A, соединяем отрезком а 1j a 2j. Таким образом, будут построены п отрезков, представляющих собой графики и линейных функций
где Р= (1 — р, р) — смешанная стратегия игрока А. 6. Если все отрезки а 1j a 2j, j=1,2,..., п, неубывающие (имеют неотрицательный наклон), то стратегия А 2доминирует стратегию А 1. Если все отрезки а 1j a 2j, j=1,2,..., п, возрастающие (имеют положительный наклон), то стратегия А 2 строго доминирует стратегию А 1. 7. Если все отрезки а 1j a 2j, j=1,2,..., п, невозрастающие (имеют неположительный наклон), то стратегия А 1доминирует стратегию А 2. Если все отрезки а 1j a 2j, j=1,2,..., п, убывающие (имеют отрицательный наклон), то стратегия А 1строго доминирует стратегию А 2.
9. Находим (выделяем) нижнюю огибающую семейства отрезков 10. На нижней огибающей находим наивысшую точку (точки). 11. Абсцисса р° этой точки является вероятностью выбора игроком А чистой стратегии А2 в оптимальной смешанной стратегии Р° = (1 – р 0, р 0) 12. Ордината наивысшей точки нижней огибающей является ценой игры V. 13. Верхний из двух концов нижней огибающей (лежащих на перпендикулярах) есть нижняя цена игры в чистых стратегиях a. 14. Нижний из верхних концов отрезков а 1j a 2j, j=1,2,..., п, есть верхняя цена игры в чистых стратегиях b. 15. Элемент матрицы А, изображающая точка которого является нижней на перпендикуляре, где она лежит, и верхним концом отрезка, на котором она лежит, будет седловой точкой игры. В этом случае чистая стратегия игрока В, номер которой совпадает со вторым индексом седловой точки, является оптимальной.
На рисунке из п отрезков а 1j a 2j, j=1,2,..., п, указаны три, которые принимают участие в конструировании нижней огибающей, выделенной жирной линией; Н — наивысшая точка этой огибающей; р° — абсцисса точки N, следовательно, Р° = (1 — р°, р°) — оптимальная смешанная стратегия игрока А, цена игры К равна ординате точки N; нижняя цена игры в чистых стратегиях a = a2j2;верхняя цена игры в чистых стратегиях b = a2j1; на рисунке видно, что a < V< b.
11. Доказательство формул для нахождения цены игры в смешанных стратегиях и стратегий игрока
Доказательство Уравнения отрезков
Так как эти отрезки пересекаются в точке N, то абсцисса р 0 этой точки является решением уравнения
откуда получаем формулу
Поскольку цена игры V представляет собой ординату точки N, то для вычисления V достаточно в правую часть одного из равенств
подставить вместо р абсциссу р 0, выраженную формулой
Подставляя р = р0 в правую часть равенства
12. Теорема о необходимом и достаточном условии оптимальности смешанной стратегии игрока
Пусть через максимальную точку N нижней огибающей отрезков Для того чтобы смешанная стратегия Q°
была оптимальной, необходимо и достаточно, чтобы отрезки
|
||||
|
Последнее изменение этой страницы: 2017-01-27; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.250.86 (0.006 с.) |

 и не имеет седловой точки, то чистые стратегии А1, В1 и А2, В2 входят в соответствующие оптимальные смешанные стратегии
и не имеет седловой точки, то чистые стратегии А1, В1 и А2, В2 входят в соответствующие оптимальные смешанные стратегии  и
и 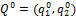 соответственно с вероятностями:
соответственно с вероятностями: 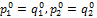 .
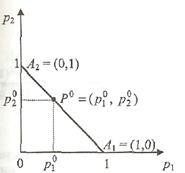
.

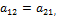 и
и 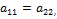 и не имеет седловой точки, то каждая чистая стратегия А1, А2, В1, В2 входит в соответствующую оптимальную стратегию
и не имеет седловой точки, то каждая чистая стратегия А1, А2, В1, В2 входит в соответствующую оптимальную стратегию 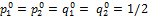 .
.
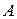 и цены игры в смешанных стратегиях в игре размерности
и цены игры в смешанных стратегиях в игре размерности 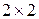 без седловой точки.
без седловой точки.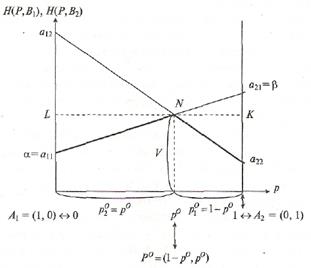

 и цены игры в смешанных стратегиях в игре размерности
и цены игры в смешанных стратегиях в игре размерности 
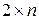 .
.

 , которая в общем случае будет представлять собой выпуклую вверх ломаную, а, в частности, может быть и отрезком.
, которая в общем случае будет представлять собой выпуклую вверх ломаную, а, в частности, может быть и отрезком.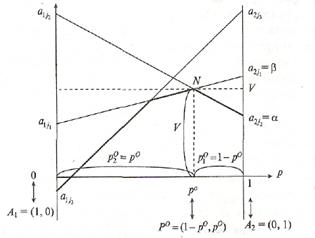



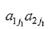 и
и 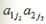 имеют следующий вид:
имеют следующий вид: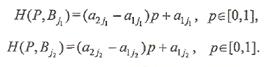
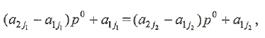
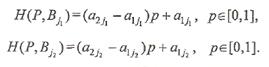
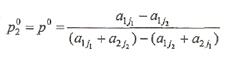 .
.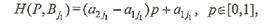 , получим
, получим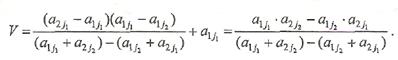
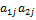 , j = 1,..., п, порождаемых чистыми стратегиями Bj, j =1,..., n, игрока В, проходят два каких-либо отрезка
, j = 1,..., п, порождаемых чистыми стратегиями Bj, j =1,..., n, игрока В, проходят два каких-либо отрезка 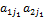 u
u 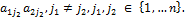
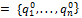 игрока B, где
игрока B, где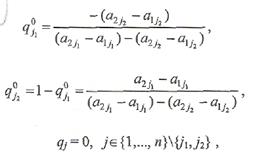
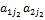 имели разные наклоны.
имели разные наклоны.


