
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи теории игр в экономике и в области финансов.Содержание книги
Поиск на нашем сайте
Классификация игр по различным признакам Теория игр- теоритич основы математич моделей принятия оптим реш-й в конфликт ситуациях рыночн отнош-й. Конфликт ситуация-это столкновение интересов не менее 2 сторон,каждая из кот для достижения целей имеет возможн действов разл способами в зависимости от действ противоборств сторон. Игройназывается упрощенная математическая модель конфликтной ситуации, отличающаяся от реального конфликта тем, что ведется по определенным правилам. Коалиция -объединение игроков по различным причинам. Правила игры- система условий с целью формализаций: а)стратегий игроков б)объем информ,кот каждый из игроков может получить от действ. др. игрока в)исход игры в рез-те любой совокупной стратегии игроков. Исход игры-набор ситуаций,образующийся в рез-те определенного хода(выбора стратегии) каждым из игроков в условиях конфликта. Стратегии-существование определенных возможных действий у каждого из игроков. Функ выигрыша игрока А→FA-это степень удовлетвор интересов игрока А. FA: X→R, X= Для игрока В-аналогично. FB-фун-я выигрыша игрока В. FB: Y→R, Y= Игры можно классифицировать по различным признакам: · по числу «игроков» (сторон)-множественные (≥2) и парные; · по числу ходов в игре: многошаговые; бесконечные; · математической структуре модели игры: рекурсивные; дифференциальные; · по числу стратегий игры: конечные; бесконечные, если хотя бы у одного «игрока» число стратегий бесконечно; · по взаимоотношениям игроков: кооперативные (коалиционные), в которых принимающие решение игроки объединены в фиксированные коалиции; члены одной коалиции могут свободно обмениваться информацией и принимать полностью согласованные решения; игроки могут вступать в коалицию и договариваться о совместных действиях бескоалиционные, в которых каждая коалиция или множество игроков, действующих совместно, состоит лишь из одного игрока; · по степени информативности «игроков» в игре: детерминированные, когда условия, в которых принимаются решения, известны полностью; стохастические, когда известно множество возможных вариантов условий и их вероятностное распределение; неопределенные, когда известно множество возможных вариантов, но без какой-либо информации об их вероятностях; · по выигрышу игры: антагонистические; игры с ненулевой суммой; · по характеру получения информации: статические игры или игры в нормальной форме (игроки получают всю предназначенную им информацию до начала игры и ходят один раз, одновременно и независимо); динамические игры или игры в позиционной форме (информация поступает игрокам в процессе развития игры); · по полноте имеющейся у игроков информации: статические игры с полной информацией статические игры с неполной информацией); динамические игры с полной информацией и неполной информацией Максиминный принцип игры Рассмотрим матричную т × п - игру с игроками А и В,в которой игрок А обладает т чистыми стратегиями
Перед игроком А стоит задача выбора чистой стратегии из множества аi 1, аi 2, …, аin, расположенных в i -й строке матрицы выигрышей, в зависимости от выбранной игроком В стратегии. Предполагая поведение игрока А крайне осмотрительным, необходимо считать, что игрок В сыграет наилучшим для себя образом и на выбор игроком А стратегии Аi выберет ту стратегию Bj, при которой выигрыш игрока А окажется минимальным. Обозначим минимальный среди выигрышей аi 1, аi 2, …, аin через α i:
и назовем его показателем эффективности стратегии Аi. Продолжая действовать разумно, игрок А должен выбрать ту стратегию, которая максимизирует показатель эффективности, т.е. для которой число α i максимально. Если обозначить это максимальное число через α:
то по формуле
Описанный принцип выбора эффективной стратегии игроком А называется максиминным принципом, а выигрыш α - максимином. Пусть игрок А выбрал максиминную стратегию
Это неравенство означает, что если игрок А в игре будет следовать максиминной стратегии, то ему при любой игре противника В гарантирован выигрыш в чистых стратегиях, не меньший максимина α.
Минимаксный принцип игры Рассмотрим матричную т × п - игру с игроками А и В,в которой игрок А обладает т чистыми стратегиями
Рассмотрим игру с точки зрения игрока В, который стремится минимизировать выигрыш игрока А, исходя из посылки, что игрок А играет наилучшим для себя и наихудшим для игрока В образом. Если игрок В выберет стратегию а 1 j , а 2 j , …, аmj, (1) выигрышей, стоящих в j -м столбце матрицы выигрышей, в зависимости от того, какой стратегии будет придерживаться игрок А. Но так как игрок В предполагает, что игрок А играет наилучшим для себя образом, то выигрышем игрока А будет максимальное из чисел (1); обозначим его через βj:
и назовем показателем неэффективности стратегии Вj. Таким образом, для любой стратегии Bj игрока В наибольший его проигрыш равен β j. В интересах игрока В - выбрать стратегию с минимальным показателем неэффективности. Наименьшее из чисел (2) обозначим β:
Отсюда в силу формулы (2) получим для β выражение:
Критерий выбора эффективной стратегии для игрока В называется минимаксным принципом, а выигрыш β называется минимаксом. Показатель эффективности смешанной стратегии игрока А относительно множества чистых стратегий игрока В. Доказательство теоремы о совпадении показателей эффективности смешанной стратегии игрока А относительно множеств смешанных и чистых стратегий игрока В Число α (P; Так как следовательно £ (P; Доказательство критерия оптимальности смешанной стратегии игрока А в терминах задаваемых цены игры в смешанных стратегиях, выигрыш-функции в смешанных стратегиях и множества смешанных стратегий игрока В. В определении равновесной ситуации в чистых стратегиях ( max (1≤i≤m)F(
29. Доказательство критерия оптимальности смешанной стратегии игрока Теорема. Для того, чтобы стратегия Qo игрока В была оптимальной, необходимо и достаточно, чтобы выполнялось неравенство H(P,Qo)≤V для любого РϵSB, т.е. выбор игроком В одной из своих оптимальных стратегий Qo гарантирует ему проигрыш, не большей цены игры V, при любой стратегии Р игрока А. Доказательство. Пусть Qo – оптимальная стратегия игрока В. Тогда по основной теореме матричных игр фон Неймана показатель эффективности β(Qo) стратегии Qo равен цене игры V: V= β(Qo). Рассматривая β(Qo) как показатель эффективности β(Qo, SA) стратегии Qo относительно множества SA смешанных стратегий игрока А, будем иметь по определению β(Qo, SA)=maxH(P,Qo). Следовательно, V= β(Qo)= β(Qo, SA)=maxH(P,Qo), откуда получаем неравенство H(P,Qo)≤V. Но V= V¾=min β(Q)≤ β(Qo). Получаем β(Qo)=V, которое в силу теоремы фон Неймана означает, что стратегия Qo являеься оптимальной. 30. Доказательство критерия оптимальности смешанной стратегии игрока Теорема. Пусть V- цена игра, H(P0,Q) – функция выигрыша, SCB={B1,…,Bn} – множество чистых стратегий игрока В. Для того чтобы стратегия Р0 игрока А была оптимальной, необходимо и достаточно, чтобы Н(Р0,Bj)≥V, j=1,…,n. Доказательство. Достаточно установить эквивалентность неравенств H(P0, Q)≥V и Н(Р0,Bj)≥V. Докажем эквивалентность. Пусть справедливо неравенство H(P0, Q)≥V. Так как это неравенство имеет место для любой стратегии QϵSB игрока В, то оно, в частности, будет справедливым и для его чистых стратегий Bjϵ SCB, j=1,…,n, т.е. неравенство Н(Р0,Bj)≥V имеет место. Таким образом импликация H(P0, Q)≥V на Н(Р0,Bj)≥V доказана. Теперь пусть имеет место неравенство Н(Р0,Bj)≥V, j=1,…,n. Тогда по формуле Н(Р0,Bj)≥V на H(P0, Q)≥V и, следовательно, эквивалентность H(P0, Q)≥V и Н(Р0,Bj)≥V.
31. Доказательство критерия оптимальности смешанной стратегии игрока Теорема. Пусть V- цена игра, H(P,Q0) – функция выигрыша, SCA={A1,…,An} – множество чистых стратегий игрока A. Для того чтобы стратегия Q0 игрока В была оптимальной, необходимо и достаточно, чтобы Н(Ai,Q0)≤V, i=1,…,n. Доказательство. Достаточно установить эквивалентность неравенств H(P,Qo)≤V и Н(Ai,Q0)≤V. Докажем эквивалентность. Пусть справедливо неравенство H(P,Qo)≤V. Так как это неравенство имеет место для любой стратегии PϵSA игрока A, то оно, в частности, будет справедливым и для его чистых стратегий Aiϵ SCA, i=1,…,n, т.е. неравенство H(P,Qo)≤V имеет место. Таким образом импликация H(P,Qo)≤V на Н(Ai,Q0)≤V доказана. Теперь пусть имеет место неравенство Н(Ai,Q0)≤V, i=1,…,n. Тогда по формуле Н(Ai,Q0)≤V на H(P,Qo)≤V и, следовательно, эквивалентность H(P,Qo)≤V и Н(Ai,Q0)≤V.
32. Доказательство теоремы о геометрической интерпретации множества стратегий игрока Следствие. Множество SOA оптимальных стратегий игрока А является выпуклым многогранником (политопом), содержащимся в симплексе SA всех смешанных стратегий игрока А. Доказательство. Для каждой оптимальной стратегии Р0=(р01,…,р0m) игрока А справедливо неравенство Н(Р0,Bj)≥V, j=1,…,n, которое можно переписать следующим образом:
33. Доказательство теоремы о геометрической интерпретации множества стратегий игрока Следствие. Множество SOВ оптимальных стратегий игрока В является выпуклым многогранником (политопом), содержащимся в симплексе SВ всех смешанных стратегий игрока В. Доказательство. Для каждой оптимальной стратегии Q0=(q01,…,q0m) игрока А справедливо неравенство Н(Ai,Q0)≤V, i=1,…,m, которое можно переписать следующим образом:
34. Доказательство в терминах множеств смешанных стратегий игроков Теорема. Для того чтобы V было ценой игры, а Р0 и Q0 – оптимальными стратегиями соответственно игроков А и В, другими словами, для того, чтобы {P0,Q0,V} было решеннием игры, необходимо и достаточно выполнение двойного неравенства H(P,Q0)≤V≤H(P0,Q) для любых PϵSA и QϵSB. Доказательство. Необходимость. Пусть V – цена игры и P0, Q0 – оптимальные стратегии. Тогда неравенства H(P,Qo)≤V и H(P0, Q)≥V справедливы и их можно записать в неравенство H(P,Q0)≤V≤H(P0,Q). Достаточность. Пусть для некоторого числа V и некоторых стратегий Р0 игрока А и Q0 игрока В выполняется двойное неравенство (P,Q0)≤V≤H(P0,Q). Так как это неравенство верно для любых PϵSA и QϵSB, то в частности оно будет справедливо и для Р= P0, Q= Q0: H(P0,Q0)≤V≤H(P0,Q0), т.е. V=H(P0,Q0). Тогда получим: H(P,Q0)≤ H(P0,Q0)≤H(P0,Q), PϵSA и QϵSB. max(PϵSA)H(P,Q0)≤ H(P0,Q0)≤min(QϵSB)H(P0,Q) или β(Qo)≤ H(P0,Q0)≤α(Р0). Отсюда по определению верхней и нижней цен игры получим: V¾=min(QϵSB)β(Q)≤ β(Qo)≤ H(P0,Q0)≤α(Р0)≤ max(PϵSA) α(Р)=V¾. Из H(P0,Q0)≤V≤H(P0,Q0) и V¾=min(QϵSB)β(Q)≤ β(Qo)≤ H(P0,Q0)≤α(Р0)≤ max(PϵSA) α(Р)=V¾. следует, что V – цена игры, а также справедливость равенства V= α(Р0)= β(Qo)= H(P0,Q0), которое по определению оптимальных стратегий, означает, что P0,Q0 – оптимальные стратегии соответственно игроков А и В.
35. Доказательство в терминах множеств чистых стратегий игроков Теорема. Для того, чтобы V была ценой игры, а P0,Q0 – оптимальными стратегиями соответственно игроков А и В, необходимо и достаточно выполнение двойного неравенства Н(Ai,Q0)≤V≤ Н(Р0,Bj), i=1,…,m, j=1,…,n. Доказательство. Достаточно доказать эквивалентность неравенств H(P,Q0)≤V≤H(P0,Q) и Н(Ai,Q0)≤V≤ Н(Р0,Bj). Пусть справедливо неравенство H(P,Q0)≤V≤H(P0,Q). Так как оно имеет место для любых стратегий PϵSA и QϵSB, то, в частности, оно справедливо и для любых чистых стратегий P=Ai, i=1,…,m, и Q=Bj, j=1,…,n, т.е. справедливо двойное неравенство Н(Ai,Q0)≤V≤ Н(Р0,Bj). Докажем обратное. Пусть имеет равенство Н(Ai,Q0)≤V≤ Н(Р0,Bj). Тогда из него, допустив получим:
36. Доказательство в терминах седловых точек выигрыш-функции критерия того, что число - цена игры в смешанных стратегиях, а PO и QO - стратегии, оптимальные во множестве смешанных стратегий соответственно игроков А и B. Для того чтобы V было ценой игры, а Р° и Qo — оптимальными стратегиями соответственно игроков А и В, необходимо и достаточно, чтобы (Р°, Q°) была седловой точкой выигрыш-функции Н(Р, Q) и Н(Р°, Q°) = V. Множество номеров i ∈ {1,2,…,m}, для которых pi> 0, называется спектром смешанной стратегии Р={р1,р2,…, рm) и обозначается supp Р. Таким образом, suppР = {i∈{1,2,..., m):рi>0} Чистая стратегия Ai- называется пассивной или активной относительно смешанной оптимальной стратегии Р° = (р1O,р2O,..., рmO)в зависимости от того, i не ∈supp Р° или i∈supp Р°, т.е. в зависимости от того, pi0 = 0 или рi0> 0.
Следствие 1
1. Если k-я строка матрицы игры доминируется некоторой другой строкой, то существует оптимальная смешанная стратегия игрока А, относительно которой чистая стратегия Аk является пассивной, т.е. входит в эту смешанную стратегию с нулевой вероятностью. 2. Если к-я строка матрицы игры строго доминируется некоторой другой строкой, то относительно любой оптимальной смешанной стратегии игрока Ak-я чистая стратегия Аk является пассивной, т.е. входит в любую смешанную стратегию с нулевой вероятностью. 3. Если l-й столбец матрицы игры доминируется некоторым другим столбцом, то существует оптимальная смешанная стратегия игрока В, относительно которой чистая стратегия Bl является пассивной, т.е. входит в эту смешанную стратегию с нулевой вероятностью. 4. Если l-й столбец матрицы игры строго доминируется некоторым другим столбцом, то относительно любой оптимальной смешанной стратегии игрока В чистая стратегия Bl является пассивной, т.е. входит в любую оптимальную смешанную стратегию с нулевой вероятностью. Следствие 1 1. Если k-я строка матрицы игры доминируется некоторой другой строкой, то существует оптимальная смешанная стратегия игрока А, относительно которой чистая стратегия Аk является пассивной, т.е. входит в эту смешанную стратегию с нулевой вероятностью. 2. Если к-я строка матрицы игры строго доминируется некоторой другой строкой, то относительно любой оптимальной смешанной стратегии игрока Ak-я чистая стратегия Аk является пассивной, т.е. входит в любую смешанную стратегию с нулевой вероятностью. 3. Если l-й столбец матрицы игры доминируется некоторым другим столбцом, то существует оптимальная смешанная стратегия игрока В, относительно которой чистая стратегия Bl является пассивной, т.е. входит в эту смешанную стратегию с нулевой вероятностью. 4. Если l-й столбец матрицы игры строго доминируется некоторым другим столбцом, то относительно любой оптимальной смешанной стратегии игрока В чистая стратегия Bl является пассивной, т.е. входит в любую оптимальную смешанную стратегию с нулевой вероятностью. Доказательство. Необходимость. Пусть i, k Î{1, 2}, i Так как чистую оптимальную стратегию Ai можно рассматривать как смешанную оптимальную стратегию, в которую чистая стратегия Ai входит достоверно, т. е. с вероятностью, равной 1, а чистая стратегия Ak – cнулевой вероятностью, то стратегия Аk является пассивной, и необходимость доказана. Отметим, что из того, что Достаточность. Пусть одна из чистых стратегий, например, стратегия Аk игрока А является пассивной. Тогда найдется оптимальная смешанная стратегия Р0 игрока А, в которую чистая стратегия Аk входит с нулевой вероятностью и, следовательно, чистая стратегия Аk входит с вероятностью, равной единице. Это означает, что Р0 = Ai, т. е. Ai – оптимальная стратегия. Пусть Q0 – некоторая оптимальная стратегия игрока В, в которую чистые стратегии Вj и Вl входят соответственно с вероятностями q0 и 1 – q0. Так как q0+( 1 – q0) = 1, то хотя бы одно из чисел q0 и 1 – q0 положительно. Если q0 = 1и, следовательно, 1 – q0 = 0, то чистая стратегия Вj является активной и тогда, по теореме об активных стратегиях
где V- цена игры. В то же время стратегия Bj является оптимальной, так как в случае q0 = 1, имеет место равенство Bj = Q0, a Q0 – оптимальная стратегия. Из равенства Если q0 = 0 и, следовательно, 1 – q0 = 1, то чистая стратегия Вj является активной оптимальной стратегией и тогда из равенства
которое имеет место в силу теоремы об активных стратегиях, следует, что Наконец, рассмотрим случай q0 > 0 и 1 – q0 > 0. В этом случае стратегии Bj и Bl активны и тогда по теореме об активных стратегиях имеют место оба равенства Могут представиться две возможности:
и
1) Рассмотрим возможность В силу (1) и (2) для показателя эффективности стратегии Аi будем иметь
Из неравенства (3) и равенства (1) следует, что
Из (5) и (6) получаем двойное равенство
которое означает, что Ai и Bj - оптимальные стратегии. Следовательно, 2) Рассмотрим возможность Если 4. Доказательство теоремы о признаке (достаточном условии) существования седловой точки матрицы игры размерности
Для того чтобы у матрицы А размером 2x2 существовала седловая точка, достаточно, чтобы сумма элементов главной диагонали матрицы А равнялась сумме элементов ее побочной диагонали:
Доказательство. Из равенства Возможны случаи:
В случае (1) из Если же имеет место случай (2), то из
5. Вывод формул для нахождения оптимальных смешанных стратегий игрока
Так как матрица А не имеет седловой точки, то нижняя цена игры в чистых стратегиях а меньше верхней цены игры в чистых стратегиях В этом случае в соответствии со следствием
Пусть Так как матрица А не имеет седловых точек, то пассивных стратегий в игре не существует. Поэтому стратегии В 1и В 2активны. Тогда
с тремя неизвестными
в силу выполнимости условия
Тогда по формулам Крамера
получаем требуемые формулы
6. Вывод формул для нахождения оптимальных смешанных стратегий игрока
Так как матрица А не имеет седловой точки, то нижняя цена игры в чистых стратегиях а меньше верхней цены игры в чистых стратегиях В этом случае в соответствии со следствием
Пусть
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-27; просмотров: 409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.01 с.) |

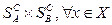 . FA(x)ЄR
. FA(x)ЄR , FB(y)ЄR.
, FB(y)ЄR.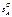 ={А1,..., Ат}, a игрок В - п чистыми стратегиями
={А1,..., Ат}, a игрок В - п чистыми стратегиями 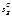 ={В1,..., Вп}. Значения функции выигрыша игрока A обозначим через аij,т. е. FA (i, j) = аij, и тогда матрица игры будет иметь вид
={В1,..., Вп}. Значения функции выигрыша игрока A обозначим через аij,т. е. FA (i, j) = аij, и тогда матрица игры будет иметь вид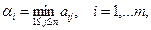
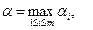
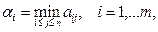
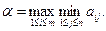
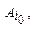 а игрок В - какую-то произвольную стратегию Bl, l = 1,..., п. Тогда в создавшейся ситуации (
а игрок В - какую-то произвольную стратегию Bl, l = 1,..., п. Тогда в создавшейся ситуации (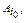 Bl) выигрыш игрока А в чистых стратегиях будет
Bl) выигрыш игрока А в чистых стратегиях будет 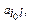 для которого в силу равенств
для которого в силу равенств 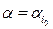 будет справедливо неравенство
будет справедливо неравенство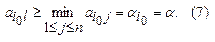
 , то выигрышем игрока А может быть один из
, то выигрышем игрока А может быть один из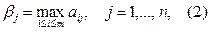
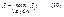

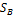 )назовем показателем эффективности смешанной стратегии PÎ
)назовем показателем эффективности смешанной стратегии PÎ 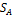 игрока A относительно множества
игрока A относительно множества 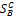 его чистых стратегий, то получим определение показателя эффективности смешанной стратегии PÎ
его чистых стратегий, то получим определение показателя эффективности смешанной стратегии PÎ 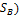 minH(P,Q) ≤ (): (QÎ
minH(P,Q) ≤ (): (QÎ  minH (P,Q) = α (P;
minH (P,Q) = α (P; 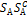 )
)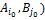 , учитывая, что(
, учитывая, что(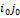 , гдеF – функция выигрыша, неравенство можно переписать в виде неравенства
, гдеF – функция выигрыша, неравенство можно переписать в виде неравенства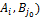 =F(
=F(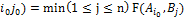 которое соответствует неравенству, а равенство в виде равенства соответствующего равенству. Это означает по данному определению седловой точки функции, что равновесная ситуация в чистых стратегиях (
которое соответствует неравенству, а равенство в виде равенства соответствующего равенству. Это означает по данному определению седловой точки функции, что равновесная ситуация в чистых стратегиях (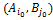 =a
=a 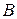 в терминах задаваемых цены игры в смешанных стратегиях, выигрыш-функции в смешанных стратегиях и множества смешанных стратегий игрока А.
в терминах задаваемых цены игры в смешанных стратегиях, выигрыш-функции в смешанных стратегиях и множества смешанных стратегий игрока А.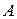 в терминах задаваемых цены игры в смешанных стратегиях, выигрыш-функции в смешанных стратегиях и множества чистых стратегий игрока
в терминах задаваемых цены игры в смешанных стратегиях, выигрыш-функции в смешанных стратегиях и множества чистых стратегий игрока 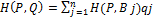 с учетом того, что
с учетом того, что  =1, получим,
=1, получим, 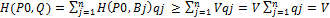 , QϵSB, т.е. доказано неравенство H(P0, Q)≥V. Таким образом, справедлива импликация
, QϵSB, т.е. доказано неравенство H(P0, Q)≥V. Таким образом, справедлива импликация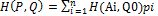 с учетом того, что
с учетом того, что 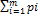 =1, получим,
=1, получим,  , PϵSA, т.е. доказано неравенство H(P,Qo)≤V. Таким образом, справедлива импликация
, PϵSA, т.е. доказано неравенство H(P,Qo)≤V. Таким образом, справедлива импликация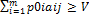 , j=1,…,n. Множество точек Р0=(р01,…,р0m) m-мерного пространства Rm, координаты p0i, i=1,…,m, которых удовлетворяет этому неравенству для фиксированного jϵ{1,…,n}, является замкнутым полупростанством, а множество точек Р0=(р01,…,p0m), координаты p0i, i=1,…,m, которых удовлетворяют этому неравенству для всех j=1,…,n, является пересечением конечного числа n замкнутых полупростанств и называется выпуклым замкнутым полиэдром. Так как к тому же множество оптимальных оптимальных стратегий игрока А SOA ограничено, поскольку оно является подмножеством симплекса всех его смешанных стратегий SA, то SOA является выпуклым многогранником.
, j=1,…,n. Множество точек Р0=(р01,…,р0m) m-мерного пространства Rm, координаты p0i, i=1,…,m, которых удовлетворяет этому неравенству для фиксированного jϵ{1,…,n}, является замкнутым полупростанством, а множество точек Р0=(р01,…,p0m), координаты p0i, i=1,…,m, которых удовлетворяют этому неравенству для всех j=1,…,n, является пересечением конечного числа n замкнутых полупростанств и называется выпуклым замкнутым полиэдром. Так как к тому же множество оптимальных оптимальных стратегий игрока А SOA ограничено, поскольку оно является подмножеством симплекса всех его смешанных стратегий SA, то SOA является выпуклым многогранником. , j=1,…,m. Множество точек Q0=(q01,…,q0m) m-мерного пространства Rm, координаты q0i, i=1,…,m, которых удовлетворяет этому неравенству для фиксированного jϵ{1,…,n}, является замкнутым полупростанством, а множество точек Q0=(q01,…,q0m), координаты q0i, i=1,…,m, которых удовлетворяют этому неравенству для всех j=1,…,n, является пересечением конечного числа n замкнутых полупростанств и называется выпуклым замкнутым полиэдром. Так как к тому же множество оптимальных оптимальных стратегий игрока B SOB ограничено, поскольку оно является подмножеством симплекса всех его смешанных стратегий SB, то SOB является выпуклым многогранником.
, j=1,…,m. Множество точек Q0=(q01,…,q0m) m-мерного пространства Rm, координаты q0i, i=1,…,m, которых удовлетворяет этому неравенству для фиксированного jϵ{1,…,n}, является замкнутым полупростанством, а множество точек Q0=(q01,…,q0m), координаты q0i, i=1,…,m, которых удовлетворяют этому неравенству для всех j=1,…,n, является пересечением конечного числа n замкнутых полупростанств и называется выпуклым замкнутым полиэдром. Так как к тому же множество оптимальных оптимальных стратегий игрока B SOB ограничено, поскольку оно является подмножеством симплекса всех его смешанных стратегий SB, то SOB является выпуклым многогранником.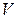 - цена игры в смешанных стратегиях, а
- цена игры в смешанных стратегиях, а 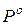 и
и 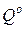 - стратегии, оптимальные во множестве смешанных стратегий соответственно игроков
- стратегии, оптимальные во множестве смешанных стратегий соответственно игроков 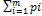 =
= 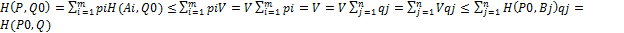 , PϵSA и QϵSB, т.е. справедливо неравенство H(P,Q0)≤V≤H(P0,Q).
, PϵSA и QϵSB, т.е. справедливо неравенство H(P,Q0)≤V≤H(P0,Q).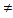 k, – номера чистых стратегий игрока А, а j, l Î{1, 2} ,j
k, – номера чистых стратегий игрока А, а j, l Î{1, 2} ,j 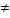 l, – номера чистых стратегий игрока В. Пусть
l, – номера чистых стратегий игрока В. Пусть 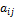 – седловая точка. Тогда Ai – оптимальная стратегия игрока А.
– седловая точка. Тогда Ai – оптимальная стратегия игрока А.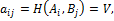 (1)
(1) с учетом оптимальности стратегий Аi и Bj следует, что
с учетом оптимальности стратегий Аi и Bj следует, что  (2)
(2)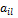 — седловая точка.
— седловая точка.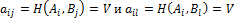 .
.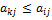 (3)
(3)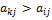 (4)
(4)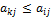 .
.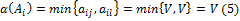

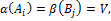
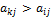 .
. , то это неравенство вместе с неравенством
, то это неравенство вместе с неравенством 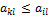 . Но так как по (2) и (1)
. Но так как по (2) и (1)  , то элемент
, то элемент 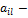 наименьший в i-й строке (на самом деле равный
наименьший в i-й строке (на самом деле равный 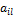 — седловая точка матрицы А.
— седловая точка матрицы А.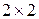 .
.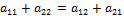
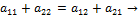

 или
или 
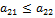 , которое вместе с неравенством (1) означает, что второй столбец матрицы А доминируется ее первым столбцом. Тогда существует оптимальная смешанная стратегия игрока В, в которую чистая стратегия В 2 входит с нулевой вероятностью (другими словами, в данном случае стратегия В 1является оптимальной). Следовательно, стратегия В 2пассивна, и потому в силу критерия седловой точки матрицы игры размерности
, которое вместе с неравенством (1) означает, что второй столбец матрицы А доминируется ее первым столбцом. Тогда существует оптимальная смешанная стратегия игрока В, в которую чистая стратегия В 2 входит с нулевой вероятностью (другими словами, в данном случае стратегия В 1является оптимальной). Следовательно, стратегия В 2пассивна, и потому в силу критерия седловой точки матрицы игры размерности 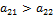 , которое вместе с (2) означает строгую юминируемость первого столбца матрицы А ее вторым столбцом. А потому В 1является пассивной и, следовательно, у матрицы А существует седловая точка.
, которое вместе с (2) означает строгую юминируемость первого столбца матрицы А ее вторым столбцом. А потому В 1является пассивной и, следовательно, у матрицы А существует седловая точка.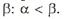 Поэтому решения игры в чистых стратегиях не существует и надо искать решение игры в смешанных стратегиях.
Поэтому решения игры в чистых стратегиях не существует и надо искать решение игры в смешанных стратегиях.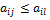 выполняется условие
выполняется условие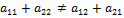 .
.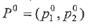 — оптимальная смешанная стратегия игрока A (которая всегда существует по основной теореме матричных игр фон Неймана) и V – цена игры.
— оптимальная смешанная стратегия игрока A (которая всегда существует по основной теореме матричных игр фон Неймана) и V – цена игры.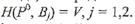 Записывая левые части этих равенств по формуле
Записывая левые части этих равенств по формуле  и присоединяя к ним нормировочное условие
и присоединяя к ним нормировочное условие 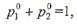 получим систему трех линейных алгебраических уравнений
получим систему трех линейных алгебраических уравнений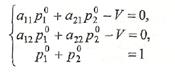
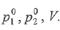 Определитель этой системы
Определитель этой системы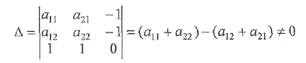
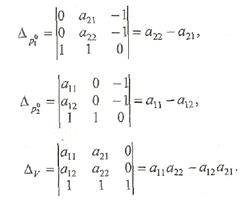
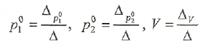
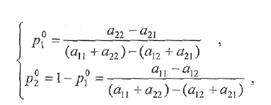 и
и 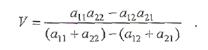
 — оптимальная смешанн
— оптимальная смешанн 


