
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация игр по различным признакамСодержание книги
Поиск на нашем сайте Теория игр- теоритич основы математич моделей принятия оптим реш-й в конфликт ситуациях рыночн отнош-й. Конфликт ситуация-это столкновение интересов не менее 2 сторон,каждая из кот для достижения целей имеет возможн действов разл способами в зависимости от действ противоборств сторон. Игройназывается упрощенная математическая модель конфликтной ситуации, отличающаяся от реального конфликта тем, что ведется по определенным правилам. Коалиция -объединение игроков по различным причинам. Правила игры- система условий с целью формализаций: а)стратегий игроков б)объем информ,кот каждый из игроков может получить от действ. др. игрока в)исход игры в рез-те любой совокупной стратегии игроков. Исход игры-набор ситуаций,образующийся в рез-те определенного хода(выбора стратегии) каждым из игроков в условиях конфликта. Стратегии-существование определенных возможных действий у каждого из игроков. Функ выигрыша игрока А→FA-это степень удовлетвор интересов игрока А. FA: X→R, X= Для игрока В-аналогично. FB-фун-я выигрыша игрока В. FB: Y→R, Y= Игры можно классифицировать по различным признакам: · по числу «игроков» (сторон)-множественные (≥2) и парные; · по числу ходов в игре: многошаговые; бесконечные; · математической структуре модели игры: рекурсивные; дифференциальные; · по числу стратегий игры: конечные; бесконечные, если хотя бы у одного «игрока» число стратегий бесконечно; · по взаимоотношениям игроков: кооперативные (коалиционные), в которых принимающие решение игроки объединены в фиксированные коалиции; члены одной коалиции могут свободно обмениваться информацией и принимать полностью согласованные решения; игроки могут вступать в коалицию и договариваться о совместных действиях бескоалиционные, в которых каждая коалиция или множество игроков, действующих совместно, состоит лишь из одного игрока; · по степени информативности «игроков» в игре: детерминированные, когда условия, в которых принимаются решения, известны полностью; стохастические, когда известно множество возможных вариантов условий и их вероятностное распределение; неопределенные, когда известно множество возможных вариантов, но без какой-либо информации об их вероятностях; · по выигрышу игры: антагонистические; игры с ненулевой суммой; · по характеру получения информации: статические игры или игры в нормальной форме (игроки получают всю предназначенную им информацию до начала игры и ходят один раз, одновременно и независимо); динамические игры или игры в позиционной форме (информация поступает игрокам в процессе развития игры); · по полноте имеющейся у игроков информации: статические игры с полной информацией статические игры с неполной информацией); динамические игры с полной информацией и неполной информацией
|
||
|
Последнее изменение этой страницы: 2017-01-27; просмотров: 467; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

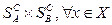 . FA(x)ЄR
. FA(x)ЄR , FB(y)ЄR.
, FB(y)ЄR.


