
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нижняя и верхняя цены игры в чистых стратегиях. Доказательство теоремы о сравнении нижней и верхней цен игры в чистых стратегиях. Цена игры в чистых стратегиях.Содержание книги
Поиск на нашем сайте
Если игрок В придерживается своей минимаксной стратегии
которое говорит о том, что игрок В, придерживаясь своей минимаксной стратегии, не может проиграть больше минимакса β независимо от действий противника А. В силу этого величина β называется верхней ценой игры в чистых стратегиях. Для нахождения нижней и верхней цен игры удобно матрицу игры увеличить в размерах, приписав (n +1)-й столбец показателей эффективности αi: стратегий Аi игрока А и (т+1)-ю строку показателей неэффективности β j стратегий Bj игрока В. В результате получим следующую матрицу:
Ниже представлена теорема, которая устанавливает соотношение между показателями эффективности α i стратегий Ai игрока А, показателями неэффективности β j стратегий Bj игрока В и выигрышами аij и, как следствие этого соотношения, - неравенство между нижней и верхней ценами игры в чистых стратегиях. Теорема: Для элементов матрицы имеют место неравенства αi ≤ aij ≤ βj, i = 1,..., m, j = 1,...,n, и, следовательно, нижняя цена игры не больше ее верхней цены в чистых стратегиях: α ≤ β. Доказательство. По определению показателей эффективности α i стратегий Аi игрока А
следовательно, неравенства αi ≤ aij ≤ βj, i = 1,..., m, j = 1,...,n, доказаны. Так как доказанное неравенство αi ≤ βj справедливо для любых i = 1,..., т, j =1,..., п, то оно будет справедливым в частности для номеров i = i0 и j = j0 соответственно максиминной и минимаксной стратегий Тогда в силу равенств Стратегии Если нижняя цена игры α равна верхней цене β, то их общее значение γ = α = β называется ценой игры в чистых стратегиях. Для того чтобы существовала цена игры в чистых стратегиях, т. е. для того чтобы нижняя цена игры α равнялась верхней цене игры β, необходимо и достаточно существование у матрицы этой игры седловой точки. 10. Понятие игровой ситуации. Игровая ситуация, удовлетворительная для игрока Ситуация – набор стратегий игроков А и В. Устойчивая ситуация или ситуация равновесия – ситуация, удовлетворительна для обоих игроков, т.е. когда игроки А и В придерживаются своих максиминной и минимаксной стратегий соответственно, то ни один из них не может увеличить свой выигрыш отступая от своей стратегии: aij0≤ai0j0≤ai0j, i=1…m, j=1,…,n, или αi0=ai0j0=βjo Неустойчивая ситуация – ситуация, сложившаяся после первых ходов игры устраивает только одного игрока, например А, тогда игрок В следующим ходом меняет свою стратегию, приводя игру к ситуации, которая не удовлетворяет игрока А. Теорема Ситуация (Ai0, Bjo) будет удовлетворительна для игрока А Тогда и только тогда, когда его выигрыш Д-во: Пусть ситауция (Ai0, Bjo) удовлетворительна для игрока А. Тогда по определению справедливо нер-во Алгоритм нахождения удовлетворительной ситуации для игрока А: 1. В каждом столбце Bj матрицы А найти max элемент βj 2. Найти строку αi, в которой находится этот элемент. 3. Тогда {Ai; Bj}является удовлетворительной для игрока А.
Причем количество удовлетворительных ситуаций для А больше числа столбцов, но меньше общего числа элементов (n ≤ NAудовл≤ mn)
11. Понятие игровой ситуации. Игровая ситуация, удовлетворительная для игрока Ситуация – набор стратегий игроков А и В. Устойчивая ситуация или ситуация равновесия – ситуация, удовлетворительна для обоих игроков, т.е. когда игроки А и В придерживаются своих максиминной и минимаксной стратегий соответственно, то ни один из них не может увеличить свой выигрыш отступая от своей стратегии: aij0≤ai0j0≤ai0j, i=1…m, j=1,…,n, или αi0=ai0j0=βjo Неустойчивая ситуация – ситуация, сложившаяся после первых ходов игры устраивает только одного игрока, например А, тогда игрок В следующим ходом меняет свою стратегию, приводя игру к ситуации, которая не удовлетворяет игрока А. Теорема. Ситуация (Ai0, Bjo) будет удовлетворительна для игрока В Тогда и только тогда, когда его проигрыш Д-во: Если ситауция (Ai0, Bjo) удовлетворительна для игрока В, то из нер-ва Если же это справедливо то по Ситуация (Ai0, Bj0) будет удовлетворительной для игрока B тогда, и только тогда, когда его проигрыш ai0j0 совпадет с показателем эффективности αi0 стратегии Ai0 игрока A: ai0j0= αi0, т.е. будет минимальным в i0-й строке матрицы игры. Алгоритм нахождения удовлетворительной ситуации для игрока В: 1) В каждой строке Ai0 матрицы игры находим наименьший элемент αi0. 2) Ищем столбец Bj0, в котором находится этот элемент. 3) (Ai0, Bj0) – удовлетворительная ситуация. Число удовлетворительных для игрока В ситуаций не меньше m и не больше mn.
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-27; просмотров: 824; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.193.223 (0.007 с.) |

 а игрок А - любой своей стратегии Ak, k = 1,..., т, то для проигрыша
а игрок А - любой своей стратегии Ak, k = 1,..., т, то для проигрыша  игрока В в ситуации (Ak,
игрока В в ситуации (Ak,  ), с использованием равенств
), с использованием равенств  и
и  , получим неравенство
, получим неравенство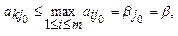
 и определению показателей неэффективности β j стратегий Bj игрока В
и определению показателей неэффективности β j стратегий Bj игрока В 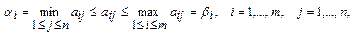
 и
и  .
. и
и  получим требуемое неравенство α ≤ β.
получим требуемое неравенство α ≤ β. и
и  игроков А и В,создающие равновесную ситуацию
игроков А и В,создающие равновесную ситуацию  , называются оптимальными. Обозначим через
, называются оптимальными. Обозначим через  и
и 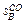 - множества чистых оптимальных стратегий соответственно игроков А и В.
- множества чистых оптимальных стратегий соответственно игроков А и В.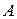 , и доказательство ее критерия. Алгоритм поиска игровых ситуаций, удовлетворительных для игрока
, и доказательство ее критерия. Алгоритм поиска игровых ситуаций, удовлетворительных для игрока  совпадет с показателем неэффективности
совпадет с показателем неэффективности  стратегии Bjo игрока В:
стратегии Bjo игрока В:  , то есть будет максимальной в j-ом столбце матрицы игры
, то есть будет максимальной в j-ом столбце матрицы игры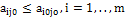 .Из этого неравенства и по определению
.Из этого неравенства и по определению  (1) показателя неэффективности стратегии Bj0 следует, что
(1) показателя неэффективности стратегии Bj0 следует, что  , то есть нер-во
, то есть нер-во  , то есть доказано
, то есть доказано 
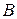 , и доказательство ее критерия. Алгоритм поиска игровых ситуаций, удовлетворительных для игрока
, и доказательство ее критерия. Алгоритм поиска игровых ситуаций, удовлетворительных для игрока  совпадет с показателем эффективности
совпадет с показателем эффективности  стратегии Aio игрока A:
стратегии Aio игрока A:  , то есть
, то есть  и равенства
и равенства  при i=i0 получим
при i=i0 получим  и рав-во
и рав-во  то есть доказано неравенство
то есть доказано неравенство 


