
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выигрыш-функция в смешанных стратегиях и различные формулы ее представления.Содержание книги
Поиск на нашем сайте
Выигрыш игрока А в ситуации (P,Q) в смешанных стратегиях представляет собой дискретную случайную величину, принимающую значения аij с вероятностью piqj. Тогда средний выигрыш игрока А в ситуации (P,Q) в смешанных стратегиях есть математическое ожидание указанной случайной величины. Функцией выигрыша игрока А в смешанных стратегиях называют функцию Н, заданную на декартовом произведении SA*SB множеств смешанных стратегий, ставящую в соответствие с каждой ситуации (P,Q)? SA*SBв смешанных стратегиях средний выигрыш игрока А в этой ситуации, определяемый как Н(P,Q)= ∑(i=1 m)∑(j=1 n)piaijqj (P,Q)?SA*SBгде Р=(p1,…, pm)Q= (q1, q2, …,qn). Данная форма задания функции выигрыша в смешанных стратегиях называется координатной. Функцию Н можно задать и в матричной форме Н(P,Q)=PAQT, где Р=(p1,…, pm) – вектор-строка размера 1хm,
- матрица игры (матрица выигрышей игрока А в чистых стратегиях) размера mxn, QT- вектор-столбец размера nx1. Для игрока А: Н(Ak,Q)=Σ(j=1,n)akjqj=AkAQT Для игрока В: H(P,Bl)=Σ(i=1,m)piail=PABlT Для функции Н можно вывести и некоторые другие формулы. Так, например, применяя матричную форму и при k=i будем иметь: H(P,Q)=PAQT=Σ(i=1,m)piH(Ai,Q) Аналогично, H(P,Q)=ΣH(P,Bj)qj 20. Показатель эффективности смешанной стратегии игрока Для каждой смешанной (в частности, чистой) стратегии P? SAигрока А существует (достигается) α (P, SB)=min(Q? SВ)H(P,Q).Число α (P, SB) – показатель эффективности смешанной стратегии P?SAигрока А относительно множества SВ смешанных стратегий игрока В. Стандартным n -симплексом называется подмножество пространства
Его вершинами являются точки:
…
Стандартным n- симплексом называется подмножество пространства Rn+1 действительных чисел, где ∆n – множество точек t0,…,tnтаких, что сумма ti=1 и для любой координаты ti≥0 Ограниченность симплекса – компакт (ограниченное замкнутое множество): рассмотрим симплекс SA(1 строчка) нормалюбого элемента определяется по правилу (2 строчка) Сначала покажем, что симплекс является ограниченным замкнутым множеством, т.е. компактом. Рассмотрим симплекс
в евклидовом пространстве
то для любой точки
означающее ограниченность симплекса Пусть последовательность точек
сходится к точке Так как
Таким образом, предельная точка Непрерывная на компакте функция достигает своих нижней и верхней границ а значит для любой P? SAнайдется хотя бы одна точка Q0?SB:α(P)=minH (P,Q)=H(P,Q0) 21. Показатель эффективности смешанной стратегии игрока Для каждой смешанной (в частности, чистой) стратегии Q? SBигрока B существует (достигается) ß (Q, SA)=max(P?SA) H(P,Q).Число ß (Q, SA) – показатель неэффективности смешанной стратегии Q? SBигрока B относительно множества SAсмешанных стратегий игрока A. Стандартным n -симплексом называется подмножество пространства
Его вершинами являются точки:
…
Стандартным n- симплексом называется подмножество пространства Rn+1 действительных чисел, где ∆n – множество точек t0,…,tnтаких, что сумма ti=1 и для любой координаты ti≥0 Ограниченность симплекса – компакт (ограниченное замкнутое множество): рассмотрим симплекс SB(1 строчка) нормалюбого элемента определяется по правилу (2 строчка) Сначала покажем, что симплекс является ограниченным замкнутым множеством, т.е. компактом. Рассмотрим симплекс
в евклидовом пространстве
означающее ограниченность симплекса Пусть последовательность точек
сходится к точке Так как
Таким образом, предельная точка Непрерывная на компакте функция достигает своих нижней и верхней границ а значит для любой Q? SBнайдется хотя бы одна точка P0?SB:α(Q)=maxH (P,Q)=F(Po,Q) Показатель эффективности смешанной стратегии игрока А относительно множества чистых стратегий игрока В. Доказательство теоремы о совпадении показателей эффективности смешанной стратегии игрока А относительно множеств смешанных и чистых стратегий игрока В Число α (P; Так как следовательно £ (P;
|
||||
|
Последнее изменение этой страницы: 2017-01-27; просмотров: 342; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.108.200 (0.005 с.) |

 ,
,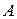 относительно множества смешанных стратегий игрока
относительно множества смешанных стратегий игрока 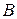 и доказательство теоремы о его существовании.
и доказательство теоремы о его существовании. действительных чисел, определяемое как
действительных чисел, определяемое как .
. ,
, ,
, .
.
 . Так как норма вектора
. Так как норма вектора  в пространстве
в пространстве  ,
, симплекса
симплекса 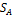 справедливо неравенство
справедливо неравенство ,
, ,
,  ,
, при
при  . Так как сходимость в
. Так как сходимость в  означает, что
означает, что  ,
,  . Поскольку
. Поскольку 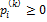 , то и
, то и  .
.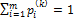 для каждого k, то
для каждого k, то .
. принадлежит симплексу
принадлежит симплексу  .
.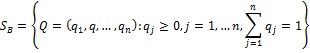
 . Так как норма вектора
. Так как норма вектора  в пространстве
в пространстве  , то для любой точки
, то для любой точки  симплекса
симплекса 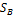 справедливо неравенство
справедливо неравенство ,
, ,
,  ,
, при
при 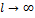 . Так как сходимость в
. Так как сходимость в  означает, что
означает, что  ,
, 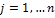 . Поскольку
. Поскольку  , то и
, то и  .
. для каждого l, то
для каждого l, то .
. принадлежит симплексу
принадлежит симплексу 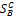 его чистых стратегий, то получим определение показателя эффективности смешанной стратегии PÎ
его чистых стратегий, то получим определение показателя эффективности смешанной стратегии PÎ 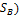 minH(P,Q) ≤ (): (QÎ
minH(P,Q) ≤ (): (QÎ  minH (P,Q) = α (P;
minH (P,Q) = α (P; 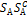 )
)


