
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доказательство критерия седловой точки матрицы игры размерности на основании принципа доминирования.Содержание книги
Поиск на нашем сайте
Теорема: Пусть i, k∈{1,2}, i ≠ k – номера строк, а j, l∈{1,2}, j ≠ l, - номера столбцов А размера 2х2. Для того, чтобы элемент aijбыл седловой точкой матрицы А, необходимо и достаточно выполнение хотя бы одного из следующих двух условий: 3. Можно удалить k-ю строку как доминируемую i-й строкой, а затем в оставшейся строке можно удалить l-й столбец как доминируемый j-м столбцом; 4. Можно удалить l-й столбец как доминируемый j-м столбцом, а затем в оставшемся j-м столбце удалить k-ю строку как доминируемую i-й строкой Доказательство. Необходимость: Пусть aij– седловая точка. Тогда элемент aij– наименьший в i-й строке и наибольший в j-ом столбце: aij≤ ail(1) aij≥ akj(2) При сравнении элементов ail и akl возможны случаи: ail≥ akl(3) и ail≤ akl (4) Рассмотрим случай (3). Неравенства (1) и (2) означают, что i-я строка доминирует k-ю строку и потому k-ю строку можно удалить. Неравенство (1) показывает, что в оставшейся i-й строке l-й столбец доминируется j-м столбцом, а потому 1-й столбец можно удалить. Таким образом, в случае (3) выполняется условие 1. Рассмотрим случай (4). Из неравенств (4), (1) и (2) следует неравенство аkl> akj, которое вместе с неравенством (1) означает, что l-й столбец доминируется j-м столбцом, и потому l-й столбец можно удалить. Неравенство (2) означает, что в оставшемся j-м столбце i-я строка доминирует k-ю строку в, следовательно, k-ю строку можно удалить. Итак, в случае выполнения неравенства (4) справедливо условие 2. Наконец, отметим, что если верны неравенства (3) и (4), т. е. если: ail= akl(5) то, как следует из доказанного, имеют место условия 1 и 2. Однако совместное выполнение условий 1 и 2 может быть и при невыполнении равенства (5). Итак, необходимость доказана. Достаточность. Пусть выполняется условие 1. Тогда i-я cтрока доминирует k-ю строку, откуда, в частности, следует, что верно (2). Так как в i-й строке l-й столбец доминируется j-м, то имеет место (1). Неравенства (1) и (2) означают, что aij - седловая точка игры. Пусть выполняется условие 2. Из того, что l-й столбец доминируется j-м столбцом, следует (1), а из того, что в j-м столбце i-я строка доминирует k-ю строку, вытекает неравенство (2). Поэтому аij - седловая точка игры. 3. Доказательство критерия седловой точки матрицы игры размерности
Для того чтобы в игре с матрицей А размера 2x2 существовала седловая точка необходимо и достаточно, чтобы одна из чистых стратегий являлась пассивной. Доказательство. Необходимость. Пусть i, k Î{1, 2}, i Так как чистую оптимальную стратегию Ai можно рассматривать как смешанную оптимальную стратегию, в которую чистая стратегия Ai входит достоверно, т. е. с вероятностью, равной 1, а чистая стратегия Ak – cнулевой вероятностью, то стратегия Аk является пассивной, и необходимость доказана. Отметим, что из того, что Достаточность. Пусть одна из чистых стратегий, например, стратегия Аk игрока А является пассивной. Тогда найдется оптимальная смешанная стратегия Р0 игрока А, в которую чистая стратегия Аk входит с нулевой вероятностью и, следовательно, чистая стратегия Аk входит с вероятностью, равной единице. Это означает, что Р0 = Ai, т. е. Ai – оптимальная стратегия. Пусть Q0 – некоторая оптимальная стратегия игрока В, в которую чистые стратегии Вj и Вl входят соответственно с вероятностями q0 и 1 – q0. Так как q0+( 1 – q0) = 1, то хотя бы одно из чисел q0 и 1 – q0 положительно. Если q0 = 1и, следовательно, 1 – q0 = 0, то чистая стратегия Вj является активной и тогда, по теореме об активных стратегиях
где V- цена игры. В то же время стратегия Bj является оптимальной, так как в случае q0 = 1, имеет место равенство Bj = Q0, a Q0 – оптимальная стратегия. Из равенства Если q0 = 0 и, следовательно, 1 – q0 = 1, то чистая стратегия Вj является активной оптимальной стратегией и тогда из равенства
которое имеет место в силу теоремы об активных стратегиях, следует, что Наконец, рассмотрим случай q0 > 0 и 1 – q0 > 0. В этом случае стратегии Bj и Bl активны и тогда по теореме об активных стратегиях имеют место оба равенства Могут представиться две возможности:
и
1) Рассмотрим возможность В силу (1) и (2) для показателя эффективности стратегии Аi будем иметь
Из неравенства (3) и равенства (1) следует, что
Из (5) и (6) получаем двойное равенство
которое означает, что Ai и Bj - оптимальные стратегии. Следовательно, 2) Рассмотрим возможность Если 4. Доказательство теоремы о признаке (достаточном условии) существования седловой точки матрицы игры размерности
Для того чтобы у матрицы А размером 2x2 существовала седловая точка, достаточно, чтобы сумма элементов главной диагонали матрицы А равнялась сумме элементов ее побочной диагонали:
Доказательство. Из равенства Возможны случаи:
В случае (1) из Если же имеет место случай (2), то из
5. Вывод формул для нахождения оптимальных смешанных стратегий игрока
Так как матрица А не имеет седловой точки, то нижняя цена игры в чистых стратегиях а меньше верхней цены игры в чистых стратегиях В этом случае в соответствии со следствием
Пусть Так как матрица А не имеет седловых точек, то пассивных стратегий в игре не существует. Поэтому стратегии В 1и В 2активны. Тогда
с тремя неизвестными
в силу выполнимости условия
Тогда по формулам Крамера
получаем требуемые формулы
6. Вывод формул для нахождения оптимальных смешанных стратегий игрока
Так как матрица А не имеет седловой точки, то нижняя цена игры в чистых стратегиях а меньше верхней цены игры в чистых стратегиях В этом случае в соответствии со следствием
Пусть Так как матрица А не имеет седловых точек, то пассивных стратегий в игре не существует. Поэтому стратегии А1и А 2активны. Следовательно, получим систему
Определитель этой системы
в силу выполнимости условия
По формулам Крамера
мы получаем формулы
|
||||
|
Последнее изменение этой страницы: 2017-01-27; просмотров: 678; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.135.201 (0.009 с.) |

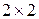 в терминах пассивных стратегий.
в терминах пассивных стратегий.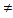 k, – номера чистых стратегий игрока А, а j, l Î{1, 2} ,j
k, – номера чистых стратегий игрока А, а j, l Î{1, 2} ,j 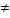 l, – номера чистых стратегий игрока В. Пусть
l, – номера чистых стратегий игрока В. Пусть 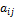 – седловая точка. Тогда Ai – оптимальная стратегия игрока А.
– седловая точка. Тогда Ai – оптимальная стратегия игрока А.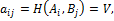 (1)
(1) с учетом оптимальности стратегий Аi и Bj следует, что
с учетом оптимальности стратегий Аi и Bj следует, что  (2)
(2)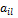 — седловая точка.
— седловая точка.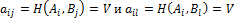 .
.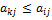 (3)
(3)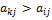 (4)
(4)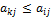 .
.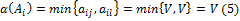

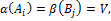
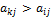 .
. , то это неравенство вместе с неравенством
, то это неравенство вместе с неравенством 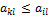 . Но так как по (2) и (1)
. Но так как по (2) и (1)  , то элемент
, то элемент 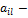 наименьший в i-й строке (на самом деле равный
наименьший в i-й строке (на самом деле равный 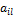 — седловая точка матрицы А.
— седловая точка матрицы А.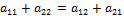
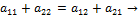

 или
или 
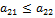 , которое вместе с неравенством (1) означает, что второй столбец матрицы А доминируется ее первым столбцом. Тогда существует оптимальная смешанная стратегия игрока В, в которую чистая стратегия В 2 входит с нулевой вероятностью (другими словами, в данном случае стратегия В 1является оптимальной). Следовательно, стратегия В 2пассивна, и потому в силу критерия седловой точки матрицы игры размерности
, которое вместе с неравенством (1) означает, что второй столбец матрицы А доминируется ее первым столбцом. Тогда существует оптимальная смешанная стратегия игрока В, в которую чистая стратегия В 2 входит с нулевой вероятностью (другими словами, в данном случае стратегия В 1является оптимальной). Следовательно, стратегия В 2пассивна, и потому в силу критерия седловой точки матрицы игры размерности 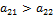 , которое вместе с (2) означает строгую юминируемость первого столбца матрицы А ее вторым столбцом. А потому В 1является пассивной и, следовательно, у матрицы А существует седловая точка.
, которое вместе с (2) означает строгую юминируемость первого столбца матрицы А ее вторым столбцом. А потому В 1является пассивной и, следовательно, у матрицы А существует седловая точка.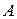 и цены игры размерности
и цены игры размерности 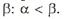 Поэтому решения игры в чистых стратегиях не существует и надо искать решение игры в смешанных стратегиях.
Поэтому решения игры в чистых стратегиях не существует и надо искать решение игры в смешанных стратегиях.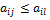 выполняется условие
выполняется условие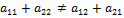 .
.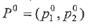 — оптимальная смешанная стратегия игрока A (которая всегда существует по основной теореме матричных игр фон Неймана) и V – цена игры.
— оптимальная смешанная стратегия игрока A (которая всегда существует по основной теореме матричных игр фон Неймана) и V – цена игры.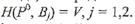 Записывая левые части этих равенств по формуле
Записывая левые части этих равенств по формуле  и присоединяя к ним нормировочное условие
и присоединяя к ним нормировочное условие 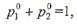 получим систему трех линейных алгебраических уравнений
получим систему трех линейных алгебраических уравнений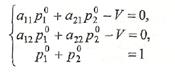
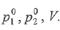 Определитель этой системы
Определитель этой системы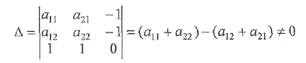
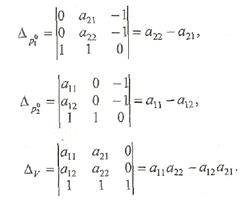
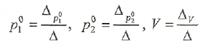
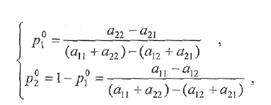 и
и 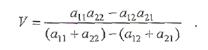
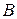 и цены игры размерности
и цены игры размерности  — оптимальная смешанная стратегия игрока В (которая всегда существует по основной теореме матричных игр фон Неймана) и V – цена игры.
— оптимальная смешанная стратегия игрока В (которая всегда существует по основной теореме матричных игр фон Неймана) и V – цена игры.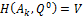 . Записывая левые части этих равенств по формуле
. Записывая левые части этих равенств по формуле 
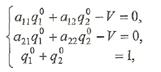 .
.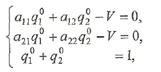 имеет единственное решение, которое можно найти по формулам Крамера. Для этого вычислим определители
имеет единственное решение, которое можно найти по формулам Крамера. Для этого вычислим определители

 и
и 



