
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование механических систем на графах связейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При моделировании механических систем естественно интерпретировать усилие
где
где Узел общего потока (1-узел) идеально подходит для того, чтобы отобразить принцип Даламбера: равенство нулю суммы всех внешних сил и силы инерции (рис. 2.10). Этот граф является, в сущности, моделью динамики тела с массой
Рис. 2.10. Графическая интерпретация принципа Даламбера Одновременно 1-узел можно использовать в качестве узла жесткого соединения твердых тел, при котором они, по существу, становится единым телом. Действительно, 1-узел – это узел общего потока, что в принятой терминологии соответствует общей (равной) скорости для всех связей 1–узла, а равенство скоростей означает движение двух тел как единого целого. Два эквивалентных графа на рис. 2.11 иллюстрирует такую связь твердых тел с массами
Рис. 2.11. Жесткое соединение тел
Отметим, что граф, приведенный на рис. 2.11,а, наглядно демон-стрирует также третий закон Ньютона о том, что действие равно противодействию. Действительно, сила В противоположность 1-узлу узел общего усилия (0-узел) можно считать узлом свободного соединения твердых тел. На рис. 2.12 показано, что соединение двух тел через 0-узел позволяет каждому телу иметь свою скорость (
Поэтому 0-узел можно использовать при моделировании упругих связей и трения, которые появляются лишь при наличии относительного движения двух тел.
Рис. 2.12. Подвижное соединение тел
Рассмотрим физический смысл других элементов ГС, которые при моделировании механических систем связываются с 0-узлом. Уравнение емкости для поступательного движения приобретает вид:
Если его проинтегрировать, то можно получить привычную форму записи закона Гука
где
Учитывая свойства 0-узла, пружину можно представить графом, приведенным на рис. 2.13,а.
Рис. 2.13. Подвижное соединение твердых тел: a – идеальная пружина, b – источник механической энергии, c – демпфер, d – пружина с внутренним трением
Как уже отмечалось выше, 0-узел необходим и для моделирования трения между двумя движущимся относительно друг друга твердыми телами (рис.2.13,b). Уравнение элемента потерь при вязком трении может иметь вид
где В общем случае зависимость силы трения от скорости может быть и нелинейной. Узел общего усилия с элементом потерь может отражать не только естественно существующее трение, но и специально вводимые в некоторые механизмы устройства: демпферы, амортизаторы. Подобно упругости и трению моделируются в механических системах источники энергии (рис. 2.13,с). В большинстве случаев источник механического движения, воздействуя на некоторое тело, одновременно создает равное, но противоположное по знаку усилие на свою опору. В относительном движении могут одновременно проявляться несколько эффектов. Например, при моделировании реальных пружин иногда требуется учитывать потери энергии за счет внутреннего трения в материале пружины. Граф пружины с внутренним трением можно представить параллельно соединенными моделями идеальной пружины и демпфера (рис. 2.13,d) или эквивалентным графом, который приведен на рис. 2.13,e. Очевидно, что элементы Рассмотрим моделирование поступательного движения трех ваго-неток, из которых две, массой
Рис. 2.14. Граф механической системы: a) кинематическая схема, b) исходный граф, c) упрощенный граф
Источник усилия
Строго говоря, неподвижное основание тоже представляет собой твердое тело с очень большой массой и может быть представлено в графе 1-узлом с подключенной к нему инерционностью. Однако этот узел является узлом общего потока (скорости), принимаемого равным нулю. Поэтому связи с неподвижным основанием, а также все связи 1-узлов, соединенных с неподвижным основанием, имеют нулевую мощность и, следовательно, могут быть исключены из графа. Таким образом, граф, полученный после эквивалентных преобразований, приведен на рис. 2.14,с. Свойство связей с неподвижным основанием в механических системах аналогично свойству связей с общей точкой (массой) в электрических системах. Различие состоит только в том, что в ГС электрической системы исключается 0-узел (узел общего нулевого потенциала). Получить полную аналогию можно было бы, применяя при моделировании механических систем дуальную интерпретацию: считать силу потоком, а скорость усилием. В этом случае инерционность Приведенный на рис. 2.15 пример иллюстрирует моделирование вертикальных движений подвески автомобиля.
Рис. 2.15 Механическая система с поступательным перемещением
Граф связей приведен на рис. 2.15,b. Здесь предполагается, что источник усилия движется вместе с массой Еще один простой пример моделирования рычага представлен на рисунке 2.16. Сила
Рис. 2.16. Кинематическая схема и граф рычага
Рассмотренная методика моделирования одномерного поступательного движения механических систем может быть без труда распространена и на системы с вращательным движением. В этом случае роль силы Приведенный на рис. 2.17 пример иллюстрирует построение ГС для узла передачи вращательного движения, включающего одну ступень редуктора с зубчатыми колесами и упругие валы
Рис. 2.17. Механическая вращающаяся система
Способ моделирования зубчатого соединения в рассмотренном примере справедлив, если основание неподвижно. В случае, когда редуктор установлен на подвижном основании, как показано на рис. 1.18,а, ГС должен учитывать угловую скорость основания
Рис. 2.18. Модель с подвижным основанием Граф на рис. 1.18,b показывает связь между абсолютными скоростями w1 и w2, а граф на рис. 1.18,c – связь между скоростями колес зубчатого соединения
|
|||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 519; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.86 (0.01 с.) |

 как силу
как силу  в поступательном движении или момент силы
в поступательном движении или момент силы  во вращательном движении, а поток
во вращательном движении, а поток  – как скорость (линей-ную
– как скорость (линей-ную  или угловую
или угловую  . Тогда уравнение инерционности представляет собой не что иное, как второй закон Ньютона
. Тогда уравнение инерционности представляет собой не что иное, как второй закон Ньютона , (2.21)
, (2.21) – масса поступательно движущегося тела, или
– масса поступательно движущегося тела, или , (2.22)
, (2.22) – момент инерции тела.
– момент инерции тела.
 и
и  .
.
 действует на оба тела, но с противо-положным знаком.
действует на оба тела, но с противо-положным знаком. и
и  соответственно). При этом третья связь 0-узла характеризует относительное движение тел:
соответственно). При этом третья связь 0-узла характеризует относительное движение тел: . (2.23)
. (2.23)
 . (2.24)
. (2.24) , (2.25)
, (2.25) – жесткость пружины;
– жесткость пружины; – податливость, т.е. величина, обратная жесткости;
– податливость, т.е. величина, обратная жесткости; – деформация пружины.
– деформация пружины.
 , (2.26)
, (2.26) – коэффициент вязкого трения.
– коэффициент вязкого трения.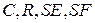 могут соединяться подобным образом в любых сочетаниях, кроме одновременного использования
могут соединяться подобным образом в любых сочетаниях, кроме одновременного использования  и
и  .
. , жестко связаны друг с другом, а между первой и второй вагонетками упруго-вязкая связь. В колесных парах присутствует трение
, жестко связаны друг с другом, а между первой и второй вагонетками упруго-вязкая связь. В колесных парах присутствует трение  . Вагонетки приводятся в движение человеком, который прикладывает к первой вагонетке силу
. Вагонетки приводятся в движение человеком, который прикладывает к первой вагонетке силу 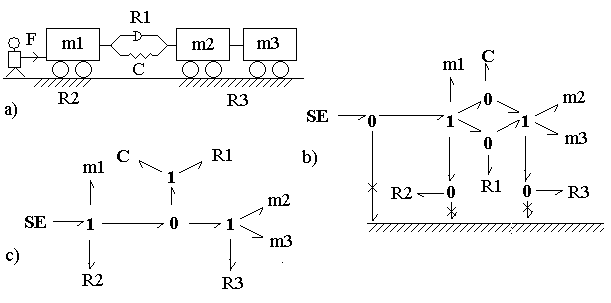
 в графах заменяется на емкость
в графах заменяется на емкость 


 .
.
 ,
,  относительно основания. Последний граф можно преобразовать к более простому виду, приведенному на рис. 1.18,d. Здесь дополнительно учтено также трение в опорах валов.
относительно основания. Последний граф можно преобразовать к более простому виду, приведенному на рис. 1.18,d. Здесь дополнительно учтено также трение в опорах валов.


