
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация методов моделирования по типу моделиСтр 1 из 31Следующая ⇒
А.В. Воронин
МОДЕЛИРОВАНИЕ МЕХАТРОННЫХ СИСТЕМ
Издательство Томского политехнического университета
Содержание
Введение
Моделирование является важнейшим и неотъемлемым этапом процедуры проектирования современных мехатронных устройств и систем. В настоящее время сложно представить себе специалиста не способного проверить моделированием обоснованность принятых технических решений. Соответственно, постоянно возрастает роль моделирования в учебном процессе. При подготовке дипломных и курсовых работ по дисциплинам, связанным с разработкой и исследованием технических устройств, этап подготовки и использования соответствующих математических моделей является одним из основных.
Формирование мехатроники можно рассматривать как продолжение и углубление процесса, который в свое время привел к появлению электромеханики, как науки, сочетающей механику и электротехнику. Развитие микроэлектроники и микропроцессорной техники создало условия для нового качественного скачка в функциональных возможностях технических систем, связанных с движением механических устройств, что привело к возникновению новой науки. Существует большое число формальных определений мехатроники и мехатронных систем, по сути, мало отличающихся друг от друга. В Государственном образовательном стандарте РФ междисциплинарной специальности 07.18 "Мехатроника" (1995 г.) оно звучит следующим образом: Мехатpоника — это новая область науки и техники, посвященная созданию и эксплуатации машин и систем с компьютеpным упpавлением движением, котоpая базиpуется на знаниях в области механики, электpоники и микpопpоцессоpной техники, инфоpматики и компьютеpного упpавления движением машин и агpегатов. Из анализа данного определения следует, что: Ø мехатронные системы предназначены, для реализации заданного движения и основу любой мехатронной системы составляет некоторый исполнительный механизм; Ø необходимой частью мехатронной системы является привод – электромеханический, гидравлический или какой-то другой; Ø важным компонентом мехатронной системы является управляющее устройство, задача которого – обеспечение сложных координированных движений механической части. Это позволяет определить особенности математических моделей мехатронных устройств, понимая под ними объекты, для исследования и проектирования которых используются математические модели, отражающие взаимное влияние протекающих в объекте процессов различной физической природы – механических, электрических, информационных и т.п. [22]. Аналогично тому, что мехатронная система это синергетическое объединение механической, электрической и компьютерной частей, средства моделирования должны допускать совместное моделирование этих частей на единой методологической основе, давая возможность строить и исследовать многоаспектные модели [30]. Реализовать это возможно двумя способами. Во-первых, можно перейти к единой системе дифференциальных уравнений, как это обычно делается в теории автоматического управления (ТАУ). В этом случае все физические особенности отдельных частей системы будут потеряны. Вариантом такого подхода является структурное моделирование, где все переменные являются скалярными сигналами и их можно соединять (как в структурной схеме). Недостаток подхода – большой объем предварительных преобразований (в случае системы уравнений), или получение схемы, мало напоминающей реальную систему.
Другой вариант – использование систем моделирования, которые способны на единой методологической основе моделировать механические, электрические и информационные компоненты, т.е. объединять их в единую схему, сохраняя при этом привычные для специалистов в предметных областях способы задания исходной информации. Описываемый подход отличается от принятого в ТАУ тем, что в математических моделях используются не абстрактные сигналы, а величины, непосредственно характеризующие физическое состояние объекта (токи, потенциалы, давления, силы и т.п.) и связанные компонентными уравнениями. Именно этот подход становится доминирующим в последнее время, и именно он является основным объектом рассмотрения в данной книге. При этом основу моделирования мехатронных систем составляет моделирование механических конструкций. Как правило, именно моделирование механических конструкций является наиболее сложным и трудоемким делом. Именно компоненты механических конструкций описываются наиболее сложными математическими моделями. Они наиболее многомерны и предъявляют наиболее жесткие требования с инструментальным средствам моделирования. Данное учебное пособие предназначено для студентов, обучающихся по направлению «Автоматизация и управление» и соответствует образовательному стандарту Томского политехнического университета по специальности 071800 – Мехатроника. Изложенный материал ориентирован на формирование у студентов знаний о современном состоянии и перспективах развития средств и методов моделирования мехатронных систем, умения ставить задачу моделирования, выбирать структуру, а также алгоритмическую и программную реализацию имитационной модели сложного динамического объекта управления; получать математические модели объектов с элементами различной физической природы и оценивать их адекватность; умения ориентироваться в средствах и методах моделирования, выбрать и настроить современную среду автоматизированного моделирования. Настоящее учебное пособие состоит из 5 частей и начинается с главы, в которой вводятся понятия модели и моделирования, перечисляются задачи, решаемые средствами моделирования, показывается роль и место моделирования в общей процедуре проектирования технических систем. Рассматриваются классификации основных методов моделирования, методов получения и исследования математических моделей с помощью ЭВМ.
Во второй главе рассматривается формализация процесса построения математических моделей мехатронных систем с использованием метода графов связей, относящегося к группе топологических методов, т.е. методов использующих графическое представление исследуемого объекта. Он основан на использовании так называемого «энергетического» подхода и позволяет на единой методологической базе строить математические модели объектов, содержащих элементы различной физической природы. Знакомство с этим методом позволит студентам лучше понять принципы построения современных систем автоматизированного моделирования. В главе 3 изложены некоторые сведения о принципах управления модельным временем и современных численных методах исследования динамических систем. Данные сведения необходимы студентам, в том числе и для того, чтобы уметь грамотно пользоваться настройками, которые допускают современные инструменты автоматизированного моделирования. Глава 4 посвящена современным компьютерным инструментам автоматизированного моделирования. Изложены основные сведения об архитектуре и принципам построения систем автоматизированного моделирования, описаны состав и функциональное назначение основных составляющих современных пакетов моделирования, а также принципы управления процессом моделирования. Глава 5 содержит обзор некоторых наиболее популярных и перспективных инструментов моделирования мехатронных систем. Коротко описаны возможности пакетов структурного (MATLAB/Simulink, VisSim, МВТУ) и физического мультидоменного моделирования (Modelica/ Dymola, 20–sim). Более детально рассмотрены расширения среды MATLAB, в частности пакет моделирования механических систем SimMechanics, электрических систем SimPower, а также пакет событийного моделирования StateFlow. Показано, что комплексирование возможностей этих пакетов на базе пакета Simulink, позволяет получить мощный инструмент исследования сложных мехатронных систем. ГЛАВА 1
ОПРЕДЕЛЕНИЕ И НАЗНАЧЕНИЕ МОДЕЛИРОВАНИЯ 1.1. Общие определения С моделированием любой человек сталкивается постоянно, обычно не осознавая этого. Действия пешехода при переходе улицы базируется на построении некоторой модели дорожной обстановки и прогнозе ее развития. От того, насколько верно пешеход воспринимает окружающую действительность, очень часто зависит не только его благополучие и здоровье, но и сама жизнь. В процессе профессиональной деятельности, если она связана с проектированием и эксплуатацией современных технических объектов и систем, исследователь постоянно вынужден иметь дело с построением и исследованием моделей этих объектов. Сейчас моделирование представляет собой основной научный инструмент, применяемый как для чисто теоретических, так и для практических целей. Создание нового технического объекта – сложный и длительный процесс, в котором стадия проектирования имеет решающее значение в осуществлении замысла и достижении высокого технического уровня. Моделирование, в свою очередь, является одним из важнейших этапов проектирования любого технического объекта, позволяя заменить или значительно сократить этапы наладки и натурных испытаний. Роль моделирования особенно высока, когда натурные испытания слишком дороги или опасны, как это имеет место, например, для космических аппаратов, химических и ядерных реакторов и других объектов.
Термин «моделирование» весьма многогранен и разными людьми воспринимается по разному. Применительно к техническим (в том числе мехатронным) системам, под моделированием будем понимать процесс, состоящий в выявлении основных свойств исследуемого объекта, построении моделей и их применении для прогнозирования поведения объекта. Таким образом, моделирование включает в себя отображение проблемы из реального мира в мир моделей (процесс абстракции), анализ и оптимизацию модели, нахождение решения и отображение решения обратно в реальный мир. Следует отметить, что в иностранной литературе то, что выше определено как моделирование, покрывается двумя терминами: Ø • «мodeling» – относится, прежде всего, к процессу построения моделей объектов и систем; Ø • «simulation» – обозначает проведение компьютерного эксперимента с моделью (обычно численного), с визуализацией результатов этого эксперимента. Моделирование, как процесс, имеет дело с моделями.Модель – создаваемое человеком подобие изучаемых объектов: макеты, изображения, схемы, словесные описания, математические формулы, карты и т.д. Более строго, модель можно определить как физическую или математическую конструкцию, определенным образом отражающую объект и служащую для его изучения. Модель является заменителем реального объекта, обладающим, по крайней мере, двумя свойствами: Ø она отражает те свойства объекта, которые существенны для данного исследования; Ø всегда проще объекта. Теория замещения одних объектов (оригиналов) другими объектами (моделями) и исследование свойств объектов на их моделях называется теорией моделирования. Тот факт, что модель отражает лишь важнейшие для данного исследования свойства объекта, дает возможность соотнести одну и ту же модель с целым рядом конкретных объектов, что позволяет по установленным свойствам одного объекта судить о свойствах больших групп объектов, подобных первому объекту. Полученные модели можно использовать для следующих целей. Познание (изучение объекта). Одной из особенностей хорошо построенной модели является то, что она несет в себе информации больше, чем в нее закладывалось при создании. Особенно это относится к моделям природных объектов, получаемых в результате естественнонаучных исследований. Скрытая неосознанная информация проникает в модель объективно, помимо воли исследователя. Это позволяет на основе изучения модели получать новые сведения об объекте, т.е. изучать объект, изучая его модель. Свойство модели служить источником познания называют потенциальностью. Естественно, что разные модели в разной степени «богаты» такой дополнительной информацией. Процесс познания в фундаментальных дисциплинах (физика, химия и д.р.) развивается по схеме «явление – модель – явление». Открытие и изучение нового явления приводит к построению его модели, которая, в свою очередь, позволяет предсказать новые явления. Классическим примером такой цепочки явилось открытие на основе Ньютоновского закона всемирного тяготения планеты Нептун. И в настоящее время большое число объектов в космологии появляются сначала на уровне теоретических предсказаний и лишь затем подтверждаются наблюдениями. Предсказание. Правильно построенная модель позволяет предсказывать поведение исследуемого объекта при тех или иных внешних воздействиях. Это свойство является ключевым в процессе замены объекта его моделью. Задача предсказания актуальна в тех случаях, когда эксперименты с реальным объектом невозможны по причинам повышенной опасности, чрезмерной длительности или невозможности воспроизведения внешних условий. Результаты предсказания могут использоваться для формирования управляющих воздействий на объект, а также для поиска оптимальных режимов работы этого объекта. Обучение. Использование реального объекта для обучения часто связано с рисками как для объекта, так и для обучаемого. Заменяя реальный объект, модели могут быть использованы в качестве имитаторов при создании различных тренажеров, на которых можно не только получить первоначальные навыки управления, но и испробовать такие приемы, которые в иной ситуации отработать невозможно. Для обучения могут использоваться как физические, так и компьютерные модели, а в сложных тренажерах сочетание тех и других. Примером могут служить тренажеры для подготовки пилотов самолетов. Кроме сложной физической системы, моделирующей кабину самолета и обладающей способностью создавать ощущение полета, имитируя движения по крену или тангажу, тренажер снабжен мощной компьютерной моделью, формирующей видеокартинки на экранах кабины и способной адекватно менять их в ответ на действия экипажа. Отработка новых конструкторских решений. С технической точки зрения возможность использования моделей для проверки и отработки технических решений является самой важной функцией моделирования. Отсутствие реального объекта делает эту функцию безальтернативной, позволяя существенно сократить время разработки нового изделия за счет экономии на его натурных испытаниях. Далее будет показано, что использование модели, для которой еще нет реального объекта, вносит существенные особенности в процесс ее построения и отладки. В зависимости от типов моделей и методов анализа их поведения различают различные методы моделирования [2,28]. Подходов к классификации этих методов достаточно много. Рассмотрим важнейшие из них.
Глава 2 Компонентное моделирование
С точки зрения уровня моделирования, мехатронные системы являются системами с сосредоточенными параметрами и относятся к макроуровню, на котором исследуемый объект имеет сложную неоднородную структуру, включающую объекты различной физической природы. Эти объекты взаимодействуют друг с другом через энергетические и информационные связи. В связи с этим серьезный интерес представляют подходы к структурированию сложных объектов. Весьма эффективен при получении моделей технических систем метод функционально законченных элементов [29]. Он основан на выделении типовых элементов технического объекта, завершенных в конструктивном отношении и предназначенных для выполнения определенных функций – двигатель, золотник, усилитель и т. д. Имея библиотеку математических моделей функционально законченных элементов и зная структуру технического объекта, можно составить его полную математическую модель. Однако отдельный функциональный элемент может также представлять собой достаточно сложный объект. Ничто не мешает применять этот метод иерархически, т.е. строить на том же принципе модели подсистем и отдельных элементов. В результате на нижнем уровне данный метод превращается в то, что в разных источниках называется методом сосредоточенных масс [29], или мультидоменного моделирования [15]. Суть его в том, что в системе выделяются отдельные элементарные материальные элементы, рассматриваемые как носители определенных физических свойств с точки зрения генерации, накопления, передачи и преобразования энергии. Таких элементов совсем не много. В [29] они названы доменами. Каждый из энергетических доменов характеризуется двумя фазовыми переменными, одна из которых Домены составляют основу любой физической модели, но их недостаточно. Нужны еще, как минимум, модели источников энергии и преобразователей параметров потока энергии. Физические свойства элемента, в том числе и домена, описываются математической моделью, отражающей зависимость между фазовыми переменными. Эти выражения называются компонентными уравнениями. Из доменов нижнего уровня могут формироваться более сложные компоненты, характеризующие не одно, а несколько свойств объекта, описываемых системами компонентных уравнений, у которых потенциальные и потоковые переменные носят векторный характер. Процедура построения математической модели технического объекта представляет собой последовательную интерпретацию свойств этого объекта в форме некоторой структуры, состоящей из типовых компонентов. Достоинство такого подхода, обычно называемого компонентным моделированием, состоит в прозрачности процедуры, в простоте и наглядности самой модели, в легкости внесения в модель изменений, связанных с учетом или не учетом тех или иных свойств объекта. Полученная модель может служить для автоматизированного моделирования технического объекта, либо для перехода к другим традиционным формам математических моделей. Для получения полной аналитической математической модели технической системы необходимо объединить все компонентные уравнения в общую систему уравнений. Объединение осуществляется на основе физических законов, выражающих условия равновесия и непрерывности фазовых переменных. Уравнения этих законов называются топологическими уравнениями. Условия равновесия записываются для потенциальных переменных в виде Все топологические уравнения являются алгебраическими. Форма компонентных и топологических уравнений одинакова для систем различной физической природы. Полная математическая модель мехатронного объекта, полученная как объединение компонентных и топологических уравнений, представляет систему алгебраических и обыкновенных дифференциальных уравнений относительно фазовых переменных – потоков и потенциалов. Одним из эффективных методов реализации идеи компонентного моделирования на нижнем уровне (уровне энергетических доменов) является метод графов связей. Метод графов связей относится к группе топологических методов, т.е. методов, использующих графическое представление исследуемого объекта. Он позволяет на единой методологической базе моделировать объекты, содержащие элементы различной физической природы – электрические, механические, электромеханические, гидравлические, пневматические и т.д. В литературе известны применения этого метода к изучению химических и биологических систем. Для расширения сферы его применения нужно лишь найти соответствующую интерпретацию общих понятий метода в соответствующей предметной области. Метод графов связей является удобным инструментом для теоретического получения моделей компонентов. Это связано с высокой степенью формализации метода, в частности введением моделей узлов, что позволяет оперировать только компонентными уравнениями при формировании моделей сложных объектов. Для графов связей разработаны сравнительно простые процедуры перехода к традиционным моделям в форме систем дифференциальных и алгебраических уравнений, передаточных функций и структурных схем. Метод графов связей перспективен и для автоматизированного моделирования как средство для формирования моделей сложных объектов. Некоторые пакеты допускают прямое включение элементов графов связей в структурные модели систем. Наконец, метод графов связей позволяет лучше понять особенности и взаимосвязи двух основных подходов к автоматизированному моделированию мехатронных систем – структурного и физического мультидоменного (другими словами, моделирование на уровне передачи сигналов и моделирование на уровне передачи энергии), что полезно для пользователя современных систем моделирования.
2.2. Основные определения графов связей
Метод графов связей (ГС) или связных графов [26] основан на представлении о том, что любые физические процессы состоят из элементарных актов преобразования энергии. Такими элементарными процессами являются накопление энергии, диссипация (потери) энергии и преобразование энергии без потерь. Таким образом, метод ГС демонстрирует известное единство природы и протекающих в ней физических процессов. Граф связей представляет собой совокупность элементов, соответствующих основным типам преобразования энергии и изображаемых в качестве вершин графа, соединенных связями (дугами графа). Связь изображается в графе линией с полустрелкой, показывающей принимаемое при моделировании за положительное направление передачи энергии. Для каждой связи в графе определены шесть величин, три из которых являются интегральными. Каждый элемент характеризуется уравнением или системой уравнений относительно переменных относящихся к его связям. Переменные связей
Основными переменными связей являются усилие мощность
энергия
перемещение
и момент
Величина
Физическая интерпретация В форме системы уравнений Самый простой способ построения математической модели проиллюстрируем на примере электрической схемы (рис.2.21,а), граф которой приведен на рис.2.21,b. Для этого пронумеруем все связи в графе и, обозначая в связи с номером
Рис. 2.21. Электрическая схема и ее граф
где Примем начальные условия нулевыми. Тогда (2.29) удобнее рассматривать как систему операторных уравнений, где Полученные 12 уравнений с 12 неизвестными могут быть записаны в матричной форме:
Решение системы уравнений (2.29) или (2.30) позволяет найти аналитические выражения для изображений всех потоков и усилий в графе. Следует отметить, что матричная форма математической модели (2.30) более удобна при численном формировании и решении систем уравнений на ЭВМ. При обычном “ручном” моделировании решение может быть получено методом подстановок в (2.29). Например, для па-дения напряжения на резисторе
Глава 3 Временной области Динамических систем Реальные мехатронные объекты и мехатронные системы описываются, как правило, системами нелинейных алгебраических и дифференциальных уравнений. Для большинства задач, представляющих практический интерес, решение их аналитическими методами невозможно. Результаты могут быть получены путем построения приближенных решений с помощью численных методов интегрирования, в частности конечно-разностных методов. Общая идея численного интегрирования обыкновенного дифференциального уравнения (ОДУ)
заключается в том, что производится дискретизация независимой переменной - времени
где Процедура интегрирования предполагает решение полученной системы конечно-разностных уравнений для фиксированных моментов времени В теории численных методов разработано большое число различных методов интегрирования, каждому из которых соответствует своя система конечно- разностных уравнений. Общее представление о них можно получить, разделив их на группы, например, на основе следующей классификации: Ø методы явные и неявные; Ø методы одношаговые и многошаговые; Ø методы первого, второго и т.д. порядков; Ø методы с постоянным шагом и методы с автоматическим выбором шага. Методы явные и неявные
Процесс формирования математической модели для численного интегрирования обязательно включает этап алгебраизации, который состоит в преобразовании обыкновенных дифференциальных уравнений в алгебраические. Он основан на использовании одного из методов численного интегрирования. Если задано дифференциальное уравнение
и начальные условия
Определенный интеграл в (3.2) численно равен площади под кривой Приближенно эта площадь может быть вычислена как площадь прямоугольника, высота которого равна значению функции
Рис. 3.3.
Подставив в (3.2) приближенные значения интеграла, можно получить две формулы:
Выражение (3.3) представляет собой формулу явного метода Эйлера. Называется метод явным потому, что неизвестное значение Формула (3.4) соответствует неявному методу Эйлера. Здесь в правой части выражения используется неизвестное значение Более точное значение интеграла (3.2) дает метод трапеций, которому соответствует отрезок 3 на рис. 3.3. Тогда
Эта формула относится, очевидно, тоже к неявным. Для явных методов процедура формирования модели для численного интегрирования ограничивается алгебраизацией исходных дифференциальных уравнений. В частности, формула (3.3) не требует дальнейших преобразований и готова для применения.
|
|||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.108.168 (0.148 с.) |
 называется потоковой, другая
называется потоковой, другая 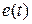 потенциальной. Произведение этих переменных всегда есть мощность. Во всех случаях домены представляют собой простые физические устройства, отражают основные физические свойства технических объектов любой физической природы – инерционные, упругие и диссипативные. С точки зрения преобразования энергии это соответствует аккумулированию кинетической энергии, аккумулированию потенциальной энергии и рассеиванию энергии.
потенциальной. Произведение этих переменных всегда есть мощность. Во всех случаях домены представляют собой простые физические устройства, отражают основные физические свойства технических объектов любой физической природы – инерционные, упругие и диссипативные. С точки зрения преобразования энергии это соответствует аккумулированию кинетической энергии, аккумулированию потенциальной энергии и рассеиванию энергии. , а условия непрерывности – для фазовых переменных типа потока
, а условия непрерывности – для фазовых переменных типа потока  . Если полная математическая модель строится вручную, топологические уравнения формируются исследователем. Если решается задача автоматизированного моделирования, эта функция возлагается на ЭВМ.
. Если полная математическая модель строится вручную, топологические уравнения формируются исследователем. Если решается задача автоматизированного моделирования, эта функция возлагается на ЭВМ.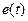 и поток
и поток 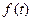 . Эти величины являются функциями времени и называются переменными мощности связи. Остальные четыре переменные вычисляются через основные по формулам:
. Эти величины являются функциями времени и называются переменными мощности связи. Остальные четыре переменные вычисляются через основные по формулам: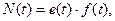 (2.1)
(2.1)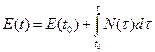 , (2.2)
, (2.2)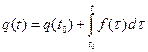 (2.3)
(2.3)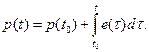 (2.4)
(2.4)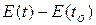 – полезная энергия, передаваемая через связь в направлении, определенном полустрелкой.
– полезная энергия, передаваемая через связь в направлении, определенном полустрелкой. поток и усилие как
поток и усилие как  и
и 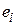 , соответственно, запишем компонентные уравнения каждого из элементов:
, соответственно, запишем компонентные уравнения каждого из элементов:
 (2.29)
(2.29)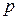 – оператор дифференцирования.
– оператор дифференцирования. (2.30)
(2.30) , последовательно исключая в (2.29) все переменные, кроме
, последовательно исключая в (2.29) все переменные, кроме  , получим
, получим

 на интервале
на интервале 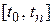 и замена ее рядом значений
и замена ее рядом значений  (принцип
(принцип  ). Расстояние между двумя соседними значениями
). Расстояние между двумя соседними значениями  называется шагом интегрирования. В частном случае он может быть постоянным на всем заданном интервале изменения переменной
называется шагом интегрирования. В частном случае он может быть постоянным на всем заданном интервале изменения переменной  . В результате, системе дифференциальных уравнений тем или иным способом ставится в соответствие система конечно- разностных уравнений
. В результате, системе дифференциальных уравнений тем или иным способом ставится в соответствие система конечно- разностных уравнений ,
, – некоторая вектор-функция, определяемая способом построения метода;
– некоторая вектор-функция, определяемая способом построения метода;  , начиная с момента
, начиная с момента  , для которого определено начальное состояние исследуемой системы
, для которого определено начальное состояние исследуемой системы  . Соответственно, решение получается в виде совокупности значений
. Соответственно, решение получается в виде совокупности значений  для заданных моментов времени.
для заданных моментов времени. (3.1)
(3.1) , то очередное значение
, то очередное значение 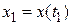 может быть получено интегрированием (3.1):
может быть получено интегрированием (3.1): (3.2)
(3.2) на интервале
на интервале  (рис. 3.2).
(рис. 3.2).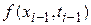 на левой границе интервала или значению
на левой границе интервала или значению  на правой границе интервала. Очевидно, площади обоих прямоугольников, ограниченных сверху отрезками 1 и 2 на рис. 3.3, будут тем ближе к точному значению интеграла, чем меньше шаг интегрирования
на правой границе интервала. Очевидно, площади обоих прямоугольников, ограниченных сверху отрезками 1 и 2 на рис. 3.3, будут тем ближе к точному значению интеграла, чем меньше шаг интегрирования  .
.
 (3.3)
(3.3) . (3.4)
. (3.4)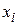 может быть непосредственно вычислено по известному значению
может быть непосредственно вычислено по известному значению  в предыдущей точке.
в предыдущей точке. . (3.5)
. (3.5)


