Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение правила циклов к графу связей
Правило циклов [24] позволяет для направленного графа или струк-турной схемы записать передаточную функцию между любыми ее входами и выходами. В соответствии с этим правилом передаточная функция графа определяется как
где Определитель графа может быть записан следующим образом:
где Поясним некоторые из используемых терминов. Циклом называется замкнутый контур в графе или структурной схеме. Передаточная функция цикла определяется как произведение передаточных функций всех звеньев, входящих в цикл. Независимыми называются циклы, не касающиеся друг друга, то есть не имеющие в структурной схеме общих точек. В формуле (2.35) – Например, в структурной схеме двигателя постоянного тока, приведенной на рис. 2.27, есть два цикла
Циклы касаются друг друга, так как имеют общий участок, вклю-чающий сумматор и звено с передаточной функцией
Рис. 2.27. Применение правила циклов к структурной схеме
Прямой путь от входного воздействия
Этот путь касается обоих циклов, поэтому сокращенный граф циклов не имеет. Тогда
Путь от возмущающего момента нагрузки
Этот путь не касается цикла
а передаточная функция двигателя по возмущению
Вся информация, необходимая для расчета передаточной функ-ции, есть, очевидно, и в графе связей, так как из него можно получить структурную схему, к тому же в различных вариантах. Рис. 2.28,а иллюстрирует поиск пути
Путь в ГС проходит вдоль связей, не меняющих направления причинности в узлах графа. Изменение причинности (то есть изменение усилия на поток и обратно) может происходить только в односвязных элементах (
Рис. 2.28. Пути и циклы в графе связей
Циклы в ГС, как это показано на рис. 1.28,с, образуются цепочками связей, сохраняющими направление причинности и заканчивающимися на обоих концах односвязными элементами Коэффициенты передачи трансформаторов и гираторов входят в передаточную функцию цикла в квадрате, поскольку цикл проходит через них дважды: один раз в прямом направлении, другой раз – в обратном. Циклы, образуемые цепочками связей, называются плоскими циклами.
Рис. 2.29. Примеры плоских циклов Рассмотрим решение задачи расчета передаточной функции механизма с редуктором, граф которого приведен на рис. 2.30.
Рис. 2.30 Циклы в графе связей
Передаточная функция единственного прямого пути
Граф содержит 5 циклов, отмеченных штриховыми линиями в графе. Передаточные функции циклов
Для того, чтобы найти все пары, тройки и т.д. не касающихся циклов, удобно построить вспомогательный граф (рис. 2.30,b), в котором каждая вершина соответствует одному из циклов, а дуга между вершинами проводится, если циклы не касаются. Каждая дуга в этом графе соответствует паре не касающихся циклов. Таких пар пять: Вспомогательный граф наглядно показывает также тройку незави-симых циклов
Путь
После необходимых подстановок получим
При использовании правила циклов необходимо учитывать, что знак передаточной функции цикла в ГС всегда отрицательный. Это следует из того, что полустрелки на концах цепочки связей в цикле, как это видно из рис. 1.29, всегда направлены в противоположные стороны. Для определения знака передаточной функции пути тоже не обязательно просматривать все изменения знака в цепочке связей, достаточно сравнить направления полустрелок в начале и конце пути.
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 307; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.216.163 (0.009 с.) |
 , (2.34)
, (2.34) – определитель графа;
– определитель графа;  – передаточная функция
– передаточная функция  -го пути между заданными входом и выходом;
-го пути между заданными входом и выходом;  – определитель сокращенного графа, образующегося в результате исключения пути с передаточной функцией
– определитель сокращенного графа, образующегося в результате исключения пути с передаточной функцией  , (2.35)
, (2.35) –
–  -е произведение передаточных функций циклов для
-е произведение передаточных функций циклов для  циклов графа, взятых из множества независимых циклов. Сумма берется по всевозможным таким комбинациям.
циклов графа, взятых из множества независимых циклов. Сумма берется по всевозможным таким комбинациям. функция
функция 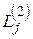 – произведение передаточных функций двух не касающихся друг друга контуров,
– произведение передаточных функций двух не касающихся друг друга контуров,  – произведение передаточных функций трех взаимно не касающихся контуров и т.д.
– произведение передаточных функций трех взаимно не касающихся контуров и т.д. и
и  с передаточными функциями
с передаточными функциями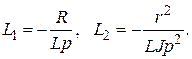
 , поэтому определитель
, поэтому определитель .
.
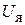 к выходной величине
к выходной величине  проходит через элементы с передаточными функциями
проходит через элементы с передаточными функциями  . Соответственно, передаточная функция этого пути равна
. Соответственно, передаточная функция этого пути равна .
. , а передаточная функция двигателя определится как
, а передаточная функция двигателя определится как .
. определяется выражением
определяется выражением .
. ,
, .
. и циклов
и циклов  ) и в гираторе.
) и в гираторе.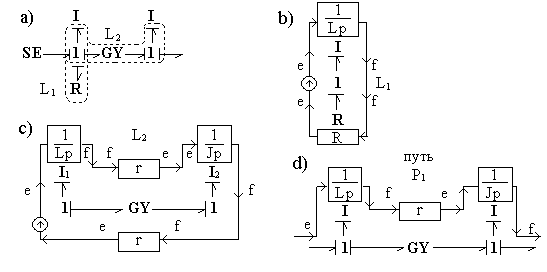



 , трансформатор
, трансформатор  , емкость
, емкость  и инерционность
и инерционность  определяется произведением переда-точных коэффициентов перечисленных элементов
определяется произведением переда-точных коэффициентов перечисленных элементов

 .
. , которая образует в треугольник. Четверок независимых циклов, которые образовали бы четырехугольник, здесь нет. Таким образом, определитель графа связей можно записать как
, которая образует в треугольник. Четверок независимых циклов, которые образовали бы четырехугольник, здесь нет. Таким образом, определитель графа связей можно записать как
 , поэтому
, поэтому  а пе-редаточная функция системы имеет вид
а пе-редаточная функция системы имеет вид .
.