
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порядок метода интегрирования.
Главный вопрос при использовании любого численного метода состоит в оценке точности приближенных вычислений · ошибка дискретизации, возникающая в результате замены дифференциального уравнения (3.1) разностной аппроксимацией (3.2); · ошибка округления, накопившаяся при выполнении арифметических операций. При этом доминирующей является, как правило, ошибка дискретизации. Будем считать, что все вычисления проводятся точно. Интуитивно ясно, что при Введем величину Очевидно, что повышение порядка метода позволяет повысить точность интегрирования при той же величине шага интегрирования Рассмотрим, например, явный одношаговый метод Хьюна (или метод Рунге-Кутты второго порядка). Он определяется формулой
Сравнивая его с методом Эйлера легко заметить, что значение Наиболее знаменитым из методов Рунге-Кутты, а возможно и из всех методов численного интегрирования, является классический метод четвертого порядка, задаваемый формулой
где
Суть метода в том, что вектор-функция правых частей системы ОДУ определяется не только в узлах сетки, но и в промежуточных точках интервала Как видно, повышение порядка метода связано с повышением затрат на вычисление значений функции Для многошаговых методов порядок напрямую связан с объемом информации, используемой на каждом шаге. В частности, двух и трехшаговые методы Адамса-Бишфорта, задаваемые формулами (3.10) и (3.11) имеют второй и третий порядок, соответственно.
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 263; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.38.125 (0.006 с.) |
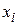 . В разделе 3.2.1 уже отмечалось, что существуют два источника погрешности при выполнении шага интегрирования:
. В разделе 3.2.1 уже отмечалось, что существуют два источника погрешности при выполнении шага интегрирования: ошибка дискретизации также должна стремиться к нулю и это действительно имеет место для любого метода. Однако взаимосвязь скорости уменьшения ошибки от скорости уменьшения
ошибка дискретизации также должна стремиться к нулю и это действительно имеет место для любого метода. Однако взаимосвязь скорости уменьшения ошибки от скорости уменьшения  для разных методов интегрирования различна.
для разных методов интегрирования различна. , называемую глобальной ошибкой дискретизации. Отметим, что
, называемую глобальной ошибкой дискретизации. Отметим, что 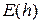 зависит от величины шага, поскольку предполагается, что значения
зависит от величины шага, поскольку предполагается, что значения  для величины, стремящейся к нулю при
для величины, стремящейся к нулю при 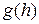 равна
равна 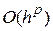 , если при
, если при  ограничена. Проведя анализ можно показать [23], что для метода Эйлера
ограничена. Проведя анализ можно показать [23], что для метода Эйлера  . Это, обычно, выражают утверждением, что метод Эйлера имеет первый порядок. Практическим следствием этого факта является то, что при уменьшении
. Это, обычно, выражают утверждением, что метод Эйлера имеет первый порядок. Практическим следствием этого факта является то, что при уменьшении 
 заменено на среднее значений функции
заменено на среднее значений функции  , вычисленных в двух различных точках. Данный метод имеет ошибку дискретизации
, вычисленных в двух различных точках. Данный метод имеет ошибку дискретизации  .
.

 , а величина
, а величина  в методе Эйлера заменена на взвешенное среднее значений
в методе Эйлера заменена на взвешенное среднее значений 


