
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналитическое моделирование мехатронных систем. Метод графов связей
Компонентное моделирование
С точки зрения уровня моделирования, мехатронные системы являются системами с сосредоточенными параметрами и относятся к макроуровню, на котором исследуемый объект имеет сложную неоднородную структуру, включающую объекты различной физической природы. Эти объекты взаимодействуют друг с другом через энергетические и информационные связи. В связи с этим серьезный интерес представляют подходы к структурированию сложных объектов. Весьма эффективен при получении моделей технических систем метод функционально законченных элементов [29]. Он основан на выделении типовых элементов технического объекта, завершенных в конструктивном отношении и предназначенных для выполнения определенных функций – двигатель, золотник, усилитель и т. д. Имея библиотеку математических моделей функционально законченных элементов и зная структуру технического объекта, можно составить его полную математическую модель. Однако отдельный функциональный элемент может также представлять собой достаточно сложный объект. Ничто не мешает применять этот метод иерархически, т.е. строить на том же принципе модели подсистем и отдельных элементов. В результате на нижнем уровне данный метод превращается в то, что в разных источниках называется методом сосредоточенных масс [29], или мультидоменного моделирования [15]. Суть его в том, что в системе выделяются отдельные элементарные материальные элементы, рассматриваемые как носители определенных физических свойств с точки зрения генерации, накопления, передачи и преобразования энергии. Таких элементов совсем не много. В [29] они названы доменами. Каждый из энергетических доменов характеризуется двумя фазовыми переменными, одна из которых
Домены составляют основу любой физической модели, но их недостаточно. Нужны еще, как минимум, модели источников энергии и преобразователей параметров потока энергии. Физические свойства элемента, в том числе и домена, описываются математической моделью, отражающей зависимость между фазовыми переменными. Эти выражения называются компонентными уравнениями. Из доменов нижнего уровня могут формироваться более сложные компоненты, характеризующие не одно, а несколько свойств объекта, описываемых системами компонентных уравнений, у которых потенциальные и потоковые переменные носят векторный характер. Процедура построения математической модели технического объекта представляет собой последовательную интерпретацию свойств этого объекта в форме некоторой структуры, состоящей из типовых компонентов. Достоинство такого подхода, обычно называемого компонентным моделированием, состоит в прозрачности процедуры, в простоте и наглядности самой модели, в легкости внесения в модель изменений, связанных с учетом или не учетом тех или иных свойств объекта. Полученная модель может служить для автоматизированного моделирования технического объекта, либо для перехода к другим традиционным формам математических моделей. Для получения полной аналитической математической модели технической системы необходимо объединить все компонентные уравнения в общую систему уравнений. Объединение осуществляется на основе физических законов, выражающих условия равновесия и непрерывности фазовых переменных. Уравнения этих законов называются топологическими уравнениями. Условия равновесия записываются для потенциальных переменных в виде Все топологические уравнения являются алгебраическими. Форма компонентных и топологических уравнений одинакова для систем различной физической природы. Полная математическая модель мехатронного объекта, полученная как объединение компонентных и топологических уравнений, представляет систему алгебраических и обыкновенных дифференциальных уравнений относительно фазовых переменных – потоков и потенциалов.
Одним из эффективных методов реализации идеи компонентного моделирования на нижнем уровне (уровне энергетических доменов) является метод графов связей. Метод графов связей относится к группе топологических методов, т.е. методов, использующих графическое представление исследуемого объекта. Он позволяет на единой методологической базе моделировать объекты, содержащие элементы различной физической природы – электрические, механические, электромеханические, гидравлические, пневматические и т.д. В литературе известны применения этого метода к изучению химических и биологических систем. Для расширения сферы его применения нужно лишь найти соответствующую интерпретацию общих понятий метода в соответствующей предметной области. Метод графов связей является удобным инструментом для теоретического получения моделей компонентов. Это связано с высокой степенью формализации метода, в частности введением моделей узлов, что позволяет оперировать только компонентными уравнениями при формировании моделей сложных объектов. Для графов связей разработаны сравнительно простые процедуры перехода к традиционным моделям в форме систем дифференциальных и алгебраических уравнений, передаточных функций и структурных схем. Метод графов связей перспективен и для автоматизированного моделирования как средство для формирования моделей сложных объектов. Некоторые пакеты допускают прямое включение элементов графов связей в структурные модели систем. Наконец, метод графов связей позволяет лучше понять особенности и взаимосвязи двух основных подходов к автоматизированному моделированию мехатронных систем – структурного и физического мультидоменного (другими словами, моделирование на уровне передачи сигналов и моделирование на уровне передачи энергии), что полезно для пользователя современных систем моделирования.
2.2. Основные определения графов связей
Метод графов связей (ГС) или связных графов [26] основан на представлении о том, что любые физические процессы состоят из элементарных актов преобразования энергии. Такими элементарными процессами являются накопление энергии, диссипация (потери) энергии и преобразование энергии без потерь. Таким образом, метод ГС демонстрирует известное единство природы и протекающих в ней физических процессов. Граф связей представляет собой совокупность элементов, соответствующих основным типам преобразования энергии и изображаемых в качестве вершин графа, соединенных связями (дугами графа). Связь изображается в графе линией с полустрелкой, показывающей принимаемое при моделировании за положительное направление передачи энергии. Для каждой связи в графе определены шесть величин, три из которых являются интегральными. Каждый элемент характеризуется уравнением или системой уравнений относительно переменных относящихся к его связям. Переменные связей
Основными переменными связей являются усилие мощность
энергия
перемещение
и момент
Величина
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 283; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.226.169 (0.008 с.) |
 называется потоковой, другая
называется потоковой, другая 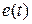 потенциальной. Произведение этих переменных всегда есть мощность. Во всех случаях домены представляют собой простые физические устройства, отражают основные физические свойства технических объектов любой физической природы – инерционные, упругие и диссипативные. С точки зрения преобразования энергии это соответствует аккумулированию кинетической энергии, аккумулированию потенциальной энергии и рассеиванию энергии.
потенциальной. Произведение этих переменных всегда есть мощность. Во всех случаях домены представляют собой простые физические устройства, отражают основные физические свойства технических объектов любой физической природы – инерционные, упругие и диссипативные. С точки зрения преобразования энергии это соответствует аккумулированию кинетической энергии, аккумулированию потенциальной энергии и рассеиванию энергии. , а условия непрерывности – для фазовых переменных типа потока
, а условия непрерывности – для фазовых переменных типа потока  . Если полная математическая модель строится вручную, топологические уравнения формируются исследователем. Если решается задача автоматизированного моделирования, эта функция возлагается на ЭВМ.
. Если полная математическая модель строится вручную, топологические уравнения формируются исследователем. Если решается задача автоматизированного моделирования, эта функция возлагается на ЭВМ.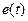 и поток
и поток 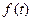 . Эти величины являются функциями времени и называются переменными мощности связи. Остальные четыре переменные вычисляются через основные по формулам:
. Эти величины являются функциями времени и называются переменными мощности связи. Остальные четыре переменные вычисляются через основные по формулам: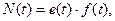 (2.1)
(2.1)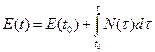 , (2.2)
, (2.2)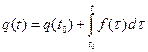 (2.3)
(2.3)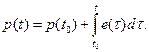 (2.4)
(2.4)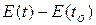 – полезная энергия, передаваемая через связь в направлении, определенном полустрелкой.
– полезная энергия, передаваемая через связь в направлении, определенном полустрелкой.


