
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логическая форма и виды сложных сужденийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Сложные суждения образуются из других суждений посредством установления логических связей между ними. Рассмотрим эти связи. · КОНЪЮНКТИВНАЯ СВЯЗЬ. В естественном языке выражается с помощью союза «и», соединяющего попарно взятые суждения. Возникающие таким образом сложные суждения именуются соединительными, или конъюнктивными, а связь между их составляющими – конъюнкцией. Пример конъюнктивной связи между суждениями: Джейн вышла замуж и у нее родился ребенок. Заменим суждение Джейн вышла замуж параметром Х, а суждение У нее родился ребенок – параметром Y. Получаем логическую форму (формулу)этого сложного суждения: «X и Y», что позволило нам отвлечься от конкретного содержания этого суждения. В естественном языке связь суждений посредством союза «и» не всегда «прозрачна», имеет несколько смысловых оттенков. Выражения вроде «Х, но и Y», «Х, несмотря на Y», «Х, хотя и Y» как раз и содержат эти различия, но при их записи в логическом языке они исчезают. Конъюнктивное суждение является истинным при одном условии: истинно и суждение Х, и суждение Y (во всех остальных случаях оно является ложным):
Данная таблица является контекстуальным определением логического смысла союза «и». Аналогичные таблицы будут построены и для других логических союзов. Конъюнкцию иногда называют логическим произведением и обозначают символом « · ДИЗЪЮНКТИВНАЯ СВЯЗЬ. В естественном языке выражается с помощью союза «или», а также союза «либо». Образующееся сложное суждение называется разделительным, или дизъюнктивным, а сама связь – дизъюнкцией. Пример: Пожар возник по причине неисправности электропроводки или он возник из-за неосторожности обращения с огнем. В отношении этого союза в обыденной речи также есть сложности: его нередко путают с другим, существенно отличающимся по роли в мышлении союзом, хотя само слово используется то же (к примеру, в предложении Петр спит или читает газету). Для различения этих двух связей первую назовем нестрогой дизъюнкцией, и логическую форму суждения с таким союзом будем представлять в виде формулы «X или Y». Нестрогою дизъюнкцию иногда называют логической суммой и обозначают символом Дизъюнктивное суждение с нестрогой дизъюнкцией ложно при одном условии: ложно и суждение Х, и суждение Y (во всех остальных случаях оно является истинным):
Вторую дизъюнктивную связь назовем строгой дизъюнкцией, и логическую формулу соответствующего суждения будем представлять в виде формулы «X либо Y». Дизъюнктивное суждение со строгой дизъюнкцией истинно при одном условии: одно и только одно из суждений – Х либо Y – должно быть ложным (во всех остальных случаях оно является ложным):
Строгая дизъюнктивная связь воспроизводится выражениями: «Х либо Y, но не оба», «или Х, или Y», «Х, кроме случая, когда Y».Символически: Дизъюнктивные суждения уместны там, где перечисляются возможные варианты исхода каких-либо событий, перечня альтернативных решений. · ИМПЛИКАТИВНАЯ СВЯЗЬ. В естественном языке её представляет выражение «если, то» или равнозначные ему «тогда, когда», «в случае, если», и др. Образующееся с его участием сложное суждение называют условным, или импликативным. Пример такого вида суждений: Если на улице идёт сильный дождь, то трава в поле мокрая. Левую часть импликативного суждения будем называть основанием, а правую – следствием. В качестве символа импликации будем использовать стрелочку: → Импликативное суждение ложно при одном условии: когда его основание Х истинно, а следствие Y ложно (во всех остальных случаях оно является истинным):
С помощью импликативных суждений можно представить любые условные зависимости, включая и причинные, например Если по проводнику течет ток, то вокруг него образуется магнитное поле. Условная связь «если, то» позволяет уточнить важное для научного и профессионального мышления понятие достаточного условия чего-либо и необходимого условия. Обстоятельство (ситуация) Х является достаточным условием обстоятельства Y, если всегда, когда имеется Х, имеется и Y. Обстоятельство (ситуация) Х является необходимым условием, если при отсутствии Х отсутствует и обстоятельство Y. Совершение убийства каким-либо человеком не является достаточным условием признания его преступником (скажем, в случае, если этот человек в момент совершения этого деяния был невменяем по независящим от него обстоятельствам). А незаконное хранение оружия достаточно для привлечения к уголовной ответственности, хотя оно не является необходимым для этого (привлечь к уголовной ответственности можно по другой причине, например, за хищение чужого имущества). · ЭКВИВАЛЕНТНАЯ СВЯЗЬ. В естественном языке эта связь воспроизводится выражениями «Х если и только если Y», «Х только тогда, когда Y», «Если Х, то Y, и если Y, то Х», «Х равносильно Y». Примеры эквивалентной зависимости суждений: Некоторое число делится на 6, если и только если оно делится на 2 и на 3. Обвиняемый может быть назван преступником только тогда, когда его деяние признано судом уголовно наказуемыми. Суждение эквивалентности ложно при ложности только одного из суждений Х или Y: во всех остальных случаях оно является истинным):
Выражение «е.т.е» является сокращением выражений «если и только если» или «только тогда, когда». Символически: ≡ В суждении эквивалентности формулируется достаточное и, одновременно, необходимое условие наступления какого-либо обстоятельства. Преступление признается совершенным группой лиц, если и только если в нём совместно участвовали два или более исполнителя. В этом суждении участие двух или более исполнителей в преступлении признается и достаточным, и необходимым условием его квалификации как совершённоё группой лиц. Как уже ранее отмечалось, суждение является либо истинным – когда то, о чем в нем «говорится», имеет место в действительности, либо ложным – когда действительность не совпадает с тем, о чем повествуется в этом суждении. Когда суждение истинно, оно составляет частицу нашего знания о мире, и тем самым помогает нам ориентироваться в нем. Спрашивается, может ли быть полезным ложное (в смысле – неистинного) суждение? Может, но при одном условии: если нам известно, что оно ложное. Из такого суждения мы, возможно, немногое узнаем о мире, но все-таки что-то узнаем, а именно: мир не таков, каким он предстает в данном суждении. Познавательную ценность ложным суждениям придает логическая связка внешнего отрицания. В обычном языке внешнее отрицание может выражаться такими словами как «неверно, что» или частицей «не», стоящими перед предложением. Естественно, прежде чем суждение может быть подвергнуто отрицанию, оно должно быть высказано как утверждение. Понятие «внешнее отрицание» отличается от того, что можно назвать внутренним отрицанием, с которым мы уже знакомы: оно входит в состав общеотрицательных, частноотрицательных и единичноотрицательных суждений в форме выражений «не есть» или «не является». Теперь построим табличное определение смысла внешнего отрицания:
Знак ┐ является обозначением выражения «Неверно, что». Из таблицы хорошо видно, что когда Х является истинным суждением, то суждение «Неверно, что Х» становится ложным; когда Х является ложным суждением, то суждение «Неверно, что Х» становится истинным. Например, суждение «Киев расположен на берегу Днепра» – истинное, а результат его отрицания – «Неверно, что Киев расположен на берегу Днепра» – ложное суждение. Аналогично, суждение «Все юристы – высококлассные специалисты» – ложное, а его отрицание «Неверно, что все юристы высококлассные специалисты» истинно. Сформулируем эквивалентности, позволяющие перенести отрицание, стоящее перед категорическим суждением, во внутреннюю его структуру, либо устранить его вовсе:
(1)Неверно, что Все S есть P эквивалентно Некоторые S не есть P
(2) Неверно, что Все S не есть P эквивалентно Некоторые S есть P
(3) Неверно, что Некоторые S есть P эквивалентно Все S не есть P (4) Неверно, что Некоторые S не есть P эквивалентно Все S есть P Данные эквивалентности можно сформулировать так: логический эквивалент категорического суждения с внешним отрицанием (правая сторона) получается заменой кванторных слов на противоположные («Все» на «Некоторые», и наоборот), и, одновременно, изменением качества отрицаемого суждения. *Рассмотрим суждение Неверно, что некоторым людям нравится болеть. Логическая форма этого суждения такова: Неверно, что некоторые S есть P где S замещает понятие «люди», а Р – «те из людей, которым нравится болеть». Следуя эквивалентности (3), получаем: Все S не есть P, что в данном конкретном случае означает: Ни одному человеку не нравится болеть. Полезно иметь в виду эквивалентности, связанные с перенесением внешнего отрицания для сложных суждений. Они таковы:
1. Неверно, что если Х, то Y эквивалентно Х и не - Y 2. Неверно, что Х и Y эквивалентно не-X или не-Y 3. Неверно, что Х или Y эквивалентно не-X и не-Y 4. Неверно, что не-X эквивалентно X Допустим, нам потребовалось преобразовать сложное суждение «Неверно, что если суд неуклонно соблюдает требования уголовного законодательства, то он может не учитывать особенности личности виновного». В соответствии с эквивалентностью 1. получаем равнозначное ему суждение «Суд неуклонно соблюдает требования уголовного законодательство, и неверно, что он не учитывает особенности личности виновного», в котором внешнее отрицание стоит уже перед простым суждением. Обратим внимание на процедуру «перевода» сложных суждений на логический язык. Такой «перевод» позволяет однозначным и наглядным образом выявить логическую форму (формулу) сложных суждений и, тем самым, уточнить в целом их содержание. Возьмем в качестве примера следующее сложное суждение: Ковалёв С.А. переведён в психический стационар(Y), поскольку его психическое расстройство является тяжелым(X). Внимательно прочитываем предложение, выражающее анализируемое суждение, и определяем его общую структуру, т.е. выделяем две его основные части (X) и (Y), и решаем, к какому из известных нам типов сложных суждений оно относится (дизъюнктивному, конъюнктивному, условному и т.п.). Устанавливаем, что это суждение является импликативным (условным): часть этого предложения, предваряемая словом «поскольку» фактически является формулировкой основания перевода пациента в психический стационар. Получаем логическую формулу анализируемого суждения: X→Y Рассмотрим еще одно сложное суждение: Умысел виновного направлен на унижение чести потерпевшего, а не на привлечение его к уголовной ответственности. Внимательное прочтение текста подскажет нам, что в целом он выражает конъюнктивное суждение, логическая форма которого имеет вид формулы Х Ù ┐Y, где Х – параметр простого суждения Умысел виновного направлен на унижение чести потерпевшего, Y – параметр простого суждения Умысел виновного направлен на привлечение его к уголовной ответственности, а символ ┐ замещает словосочетание Неверно, что. Перевод» суждений с естественного языка на логический далеко не механическая процедура. Однако после выполнения нескольких упражнений соответствующий навык вполне можно приобрести. Ранее было отмечено (раздел 1.2), что в логике, как и во всех других науках, имеются свои законы. Логический закон истолковывался как некоторая форма (схема), котораяпревращается в истинное суждение при подстановке в нее любых по содержанию конкретных суждений. Теперь имеется возможность установить в отношении любой формулы нашего логического языка: является ли она логическим законом или не является таковым? Производится это методом построения семантической таблицы. Решим этот вопрос, к примеру, в отношении формулы Х
Убеждаемся, что эта формула не является законом логики. Обратимся к формуле Х
В любой строчке данной формулы, т.е. при любых значениях Х она принимает значение «и», что и требовалось показать. В науке логики все законы (т. е. всегда истинные) формулы называют тавтологиями.
Практикум 1. Определите, из каких простых суждений составлены следующие сложные. 1. Январь и февраль – зимние месяцы. 2. Болгария расположена в Европе и является республикой. 3. Тела от холода сжимаются, а от тепла – расширяются. 4. «Если с другом вышел в путь – веселей дорога» (из песни). 5. Греки любили поболтать, зато и первыми начали философствовать. 2. Постройте логические формулы сложных суждений: а) Если человек читал книгу, то знает ее содержание. б) Неверно, что Иванов не учился в университете. в) Он был и прилежным, но большими способностями не обладал. г) На этом факультете учатся только способные студенты. д) Петров будет получать стипендию, если сдаст экзамен до завтра. е) «Когда в товарищах согласья нет, на лад их дело не пойдет» (из басни И.А.Крылова). 3. Преобразуйте следующие суждения в соответствии с эквивалентностями (1) – (4): Неверно, что есть студенты, которые опаздывают на занятия. Неверно, что любой студент охотно занимаются спортом. Неверно, что ни один студент не может выполнить это упражнение.
3.5. Модальные суждения
До сих пор речь шла только об ассерторических суждениях, т.е. таких, в которых утверждается наличие либо отсутствие некоторой ситуации (присущность какого-либо свойства предметам, нахождение их в определенных отношениях и т.п.). Однако мыслимая в ассерторическом суждении ситуация наличествует (или отсутствует) в действительности либо случайно, либо необходимо; она возможна (в будущем), или невозможна. Аналогично, поступки, действия людей, воспроизводимые ассерторическими суждениями, могут быть в обществе либо разрешены, либо запрещены, либо обязательны. Наконец, ассерторические суждения о мире могут быть доказаны или опровергнуты, либо никому не удалось сделать ни того, ни другого. Суждения, в которых содержатся подобные характеристики, или оценки ситуаций, действий и знаний, называются модальными. Слова, с помощью которых фиксируется модальность суждения (типа «необходимо», «разрешено», «доказано» и т.п.), называются модальными понятиями, или модальными терминами. Среди известных модальных понятий выделяют: 1) Алетические, содержащие оценочные понятия «необходимо», «возможно», «случайно». 2) Деонтические (от греч. deonte – как должно быть) – оценки действий и поступков людей в обществе терминами «обязательно», «разрешено», «запрещено». 3) Эпистемические (от греч. episteme – знание) – оценки наших знаний по типу «доказано», «опровергнуто», «проблематично» (в смысле «не исключено, что истинно»). Некоторые свойства приведенных модальностей могут быть уточнены путем определения логических отношений между содержащими эти термины суждений. Рассмотрим алетические модальные суждения. Пусть символ Х представляет какое-то событие, некоторую ситуацию или определенный процесс. Тогда логические формы алетических модальностей будут представлены формулами Необходимо, что Х; Возможно, что Х; Случайно, что Х, а такжеэтимиформулами, дополненными внешним отрицанием. Имеют место следующие эквивалентности (равнозначности) между алетическими модальностями: 1. Необходимо, что Х эквивалентно Неверно, что возможно не - Х 2. Случайно, что Х эквивалентно Возможно, что Х и возможно, что не - Х 3. Неверно, что необходимо Х эквивалентно Возможно, что не - Х 4. Возможно, что Х эквивалентно Неверно, что необходимо не - Х Рассмотрим пример. Известна истина Все живое – смертно. Это суждение может являться не только результатом обобщения многочисленных фактов, но и выражать некий биологический закон, природную необходимость. Поэтому его можно сформулировать как суждение алетической модальности Необходимо, что любое живое существо смертно. Этому суждению в соответствии с эквивалентностью 1. равнозначно суждение Неверно, что возможно так, что некоторые живые существа не являются смертными. Суждения с алетическими модальностями оцениваются как истинные либо ложные. Суждения с деонтическими модальностями выражают некоторые нормы. Нормы определяют, что должен (обязан) делать тот-то и тот, что и кому разрешено (запрещено). В отношении деонтических модальностей справедливы такие эквивалентности: 1. Неверно, что запрещено Х эквивалентно Разрешено, что Х 2. Обязательно, что Х эквивалентно Неверно, что разрешено не- Х 3. Запрещено, что Х эквивалентно Обязательно, что не- Х Рассмотрим суждение Преступление является уголовно наказуемым деянием. Оно не столько описывает фактическое положение дел в обществе, сколько устанавливает некую норму-требование Любое преступление подлежит соразмерному уголовному наказанию. Отсюда видно, что анализируемое суждение содержит деонтическую модальность и может быть представлено формулой Обязательно, что Х, где Х – суждение Любое преступление уголовно наказуемо. Используя эквивалентность 2., получаем равнозначное исходному суждение Неверно,что разрешено так, что некоторые преступления не подлежат уголовной ответственности. Синтаксически (грамматически) деонтические суждения могут быть выражены в форме ассерторических суждений. К примеру, в суждении Приговор выносится именем Российской Федерации формулируется, по сути дела, соответствующая правообязывающая норма, а не констатация некоторого факта. Правовые нормы можно оценивать в качестве нормативно-истинных или нормативно-ложных, если они соответствуют либо не соответствуют целям, которые ставит законодатель, выражая свою волю. Как мы помним, заблуждается тот, кто признает за истину и некоторое суждение, и его отрицание. Речь идет о законе противоречия: Неверно, что Х и не-Х Эта формула обязывает нас к признанию ложным любого суждения формы Х и не-Х. Полезно обратить внимание на формулировку этого закона применительно к суждениям с деонтической модальностью. Вот некоторые из них: 1. Неверно, что обязательно Х и разрешено не- Х 2. Неверно, что разрешено Х и запрещено Х На языке правовых норм логическую форму 1. имеет, к примеру, суждение Неверно, что каждый работающий гражданин обязан платить налоги и (в тоже время) некоторым из работающих граждан разрешено налоги не платить, а форму 2. – суждение Неверно, что всем гражданам, достигшим 18 лет, разрешено участвовать в выборах, и некоторым из них это запрещено. В законодательствах, уставах и договорах нередко встречаются логически противоречивые («конфликтующие») нормы, когда одна из них что-то запрещает, а другая это же самое разрешает; одна обязывает к какому-либо действию, а другая разрешает не совершать его. Такие деонтически противоречивые документы приводят к конфликтам между людьми, организациями и странами, в которых виноваты не столько они сами, сколько юристы, которые принимали участие в их составлении. К примеру, в Конвенции ООН по морскому праву (UNCLOS), определяющей особенности судоходства в покрытых льдами районах говорится, с одной стороны, о недискриминационном транзите судов третьих стран, а с другой – о праве прибрежных государств определять собственные стандарты. Всем людям, находящимся в здравом уме, логика не рекомендует также нарушать закон исключенного третьего: Х или не-Х в соответствии с которым если Х – истинное суждение,то отрицание того суждения даёт нам ложное суждение, и наоборот. Приведем некоторые формулировки этого закона в языке деонтических модальностей: 1. Обязательно, что Х или разрешено не- Х 2. Разрешено, что Х или запрещено Х Ясно, что одно и только одно из них – нормативно-истинное суждение. На языке правовых норм логическую форму 1. имеет, к примеру, суждение Каждый гражданин РФ мужского пола, которому исполнилось Желательно, чтобы любая социально значимая деятельность физического лица или организации имела правовую квалификацию в терминах деонтических модальностей. Однако нередко бывает так, что система правовых норм неполна, т.е. в ней прописаны законодателем правовые нормы не для всех видов социально значимой деятельности или не для всех категорий правоответственных граждан. В этих случаях трудно решить, к примеру, обязан ли гражданин делать то-то и то-то в таких-то и таких обстоятельствах, или ему разрешено не делать этого. Логические формысуждений с эпистемическими модальностями представим следующими выражениями: Доказано, что Х; Проблематично, чтоХ; Опровергнуто, что Х, а такжеэтими же выражениями, но с внешним отрицанием. В отношении этих модальностей имеем следующие логические зависимости: 1. Доказано, что Х эквивалентно Неверно, что проблематично не- Х 2. Доказано, что не- Х эквивалентно Опровергнуто, что Х 3. Проблематично, что Х эквивалентно Неверно, что доказано Х, и 4. Если доказано, что Х, то Х – истинно 5. Если опровергнуто, что Х, то Х – ложно К примеру, доказать, что подсудимый виновен – значит исключить возможность его невиновности, и обратно (согл. экв. 1). Если доказано, что подсудимый невиновен, то это означает, что опровергнуто обвинение против него; опровергнуть обвинение – значит доказать невиновность подсудимого (согл. экв. 2). Если не доказана виновность и она не опровергнута, следует считать, что виновность (либо невиновность) подсудимого не исключена, и обратно (согл. экв. 3). Если доказана виновность подсудимого, то следует полагать, что он совершил это преступление (согл. экв. 4); обратное верно не всегда. Если опровергнута виновность, то следует полагать, что подсудимый является невиновным (согл. экв. 5); обратное верно не всегда. (Логическая суть доказывания и опровержения специально будет рассматриваться в разделах 5.3.1 и 5.3.2.). Практикум 1. Определите вид модальности (выделите модальное понятие) следующих суждений; представьте логические формы этих суждений: 1) Невозможно без весел плыть против течения. 2) Проблематично, что существует творящее Мир начало (Бог). 3) Любой гражданин обязан соблюдать законы государства. 4) Доказано, что Земля вращается вокруг Солнца. 5) Необходимо, что Земля вращается вокруг своей оси. * Выполним задание в отношении суждения Не доказано и не опровергнуто, что Бог существует. Это суждение относится к эпистемическим модальным суждениям, поскольку в нем фигурируют модальные термины доказано и опровергнуто. Основу этого суждения составляет ассерторическое суждение Бог существует, которое мы заменяем параметром Х. Строим формулу этого суждения: Неверно, что доказано Х, и не опровергнуто, что Х 2. Постройте логические формулы следующих деонтических суждений: 1) Запрещается изменение стоимости утвержденных проектов за счет исключения планируемых мероприятий по охране окружающей среды. 2) Строительство зданий должно осуществляться по утвержденным проектам, имеющим положительные заключения государственной экологической экспертизы. 3) Деятельность, осуществляемая с нарушением природоохранных требований, может быть прекращена в порядке, установленном законодательством Российской Федерации. 4) При осуществлении строительства зданий принимаются меры по охране окружающей среды в соответствии с законодательством Российской Федерации. *Выполним задание в отношении суждения Государственные инспектора в области охраны окружающей среды обязаны соблюдать требования законодательства. Заменим параметром Х утверждение Государственные инспектора в области охраны окружающей среды соблюдают требования законодательства. Тогда логическая форма анализируемого суждения примет вид формулы Обязательно, что Х. Поскольку Обязательно, что Х эквивалентно Неверно, что разрешено не-Х, получаем иную, но эквивалентно формулировку исходного суждения: Неверно, что государственным инспекторам разрешено не считаться с требованиями законодательства. 3. Сформулируйте на основе суждений, приведенных в упр.2., противоречащие им суждения. *Выполним задание в отношении суждения Все граждане обязаны бережно относиться к природе, логической формой которого является выражение Обязательно, что Х. В соответствии с формулой закона противоречия Неверно, что обязательно Х и разрешено не- Х противоречить данному суждению будет суждение Разрешено некоторым гражданам не относиться рачительно к природе. 4 Имея в виду зависимости 1.-5. между эпистемическими модальностями, ответьте на следующие вопросы: 1) Эквивалентны ли (в соответствии с процессуальными правовыми нормами) суждения Доказано, что инспектор N. нарушил законодательство и Инспектор N. нарушил законодательство? 2) Эквивалентны ли суждения Опровергнуто, что инспектор N. нарушил законодательство и Инспектор N. не нарушал законодательства? 3) Следует ли логически из суждения Инспектор N. нарушил законодательство суждение Доказано, что инспектор N. нарушил законодательство?
Тема 4. УМОЗАКЛЮЧЕНИЕ
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 2206; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.234.68 (0.012 с.) |

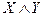
 ».
». . Дизъюнктивная связь воспроизводится также в таких выражениях как «Х или Y или оба», «Х, если не-Y».
. Дизъюнктивная связь воспроизводится также в таких выражениях как «Х или Y или оба», «Х, если не-Y».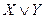
 Y
Y





