Координатная форма записи уравнений движения точки
Содержание книги
- Момент равнодействующей плоской ссс относительно любого центра, лежащего в той же плоскости, равен алгебраической сумме моментов слагаемых сил относительно того же центра.
- Момент силы относительно центра как вектор
- Фермой называется жесткая (неизменяемая) конструкция из прямолинейных стержней, соединенных на концах шарнирами.
- Лекция 6. Ведение в кинематику
- Поступательное движение тела
- Лекция 8. Сложное движение точки
- Лекция 9. 9. 1 плоскопараллельное движение тела
- Всякое элементарное перемещение тела, имеющего одну неподвижную точку, можно представить как элементарный поворот относительно мгновенной оси вращения, проходящей через эту точку.
- Скорость своего движения под действием приложенных к нему сил.
- Координатная форма записи уравнений движения точки
- Уравнение относительного движения точки
- Той же механической системы.
- Количество движения точки и импульс силы
- Ную геометрической сумме количеств движения всех точек данной системы,
- Взятого относительно какого-либо неподвижного центра, равна моменту действующей на точку силы относительно того же центра.
- ЛЕКЦИЯ 15. Принцип Даламбера
- Перемещение, которое допускается в данный момент времени наложенными на систему связями без их нарушения.
- Общие теоремы динамики при ударе
- Геометрической сумме моментов ударных импульсов, действующих на систему.
Похожие статьи вашей тематики
Для их написания воспользуемся выражением основного закона динамики в виде (11.1). Спроектировав обе части этого выражения на оси декартовой системы отсчета (рис. 12.1), получим:
| Учитывая, что
| 
| и т.д., получим:
|
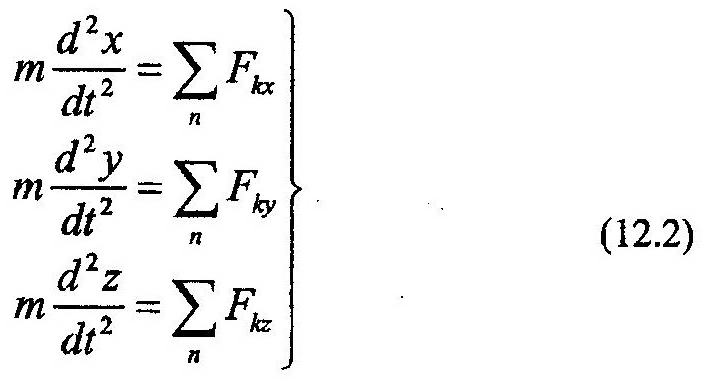
Таким образом, в декартовой системе отсчета движение точки можно описать системой трех дифференциальных уравнений второго порядка.
Естественная форма записи уравнений движения точки
В тех случаях, когда траектория движения точки определена заранее, успешно используют в решении задач естественный способ задания движения точки. Уравнения движения точки, соответствующие данному способу, получим, проектируя обе части выражения основного закона динамики (11.1) на оси τ, n, b (рис. 12.2):
В (12.4) только в первые два уравнения входит кинематический параметр, характери-зующий движение точки, это – V. Последнее выражение в (12.4) по своему виду соответствует уравнению равновесия – уравнению статики. Из всех уравнений (12.4) только первое является дифференциальным. Таким образом, уравнения движения точки, соответствующие естественному способу, являются более простыми по своему виду. В этом их преимущество над уравнениями вида (12.2).
Задачи динамики
Все задачи динамики можно условно поделить на две группы: первая (прямая) и вторая (обратная) задачи. Условность деления заключается в том, что не все задачи один к одному соответствуют формулировкам, указанным ниже. Возможно и их сочетание в пределах одной задачи.
В прямых задачах: по известным уравнениям движения точки определяют силы,вызы-
Вающие его.
Таким образом, исходными для решения первой задачи динамики точки являются ее уравнения движения, записанные в одном из видов: векторном, координатном или естественном (см. тему: «способы задания движения точки»). Например, в координатной форме записи эти уравнения связывают координаты точки (x, y, z) с временем (t).
Алгоритм решения первой (прямой) задачи представлен ниже:
По известным уравнениям движения находят вторые производные от координат по времени и, умножая их на массу точки, m, определяют правые части выражений (12.2). Модуль равнодействующей, R, системы сходящихся сил, приложенных к точке, равен длине диагонали параллелепипеда, построенного на проекциях Rx, Ry, Rz как на сторонах. С помощью направляющих косинусов можно определить направление вектора равно-действующей в пространстве.
В обратных задачах: по известным силам, действующим на точку, и начальным усло-
|