Количество движения точки и импульс силы
Содержание книги
- Момент равнодействующей плоской ссс относительно любого центра, лежащего в той же плоскости, равен алгебраической сумме моментов слагаемых сил относительно того же центра.
- Момент силы относительно центра как вектор
- Фермой называется жесткая (неизменяемая) конструкция из прямолинейных стержней, соединенных на концах шарнирами.
- Лекция 6. Ведение в кинематику
- Поступательное движение тела
- Лекция 8. Сложное движение точки
- Лекция 9. 9. 1 плоскопараллельное движение тела
- Всякое элементарное перемещение тела, имеющего одну неподвижную точку, можно представить как элементарный поворот относительно мгновенной оси вращения, проходящей через эту точку.
- Скорость своего движения под действием приложенных к нему сил.
- Координатная форма записи уравнений движения точки
- Уравнение относительного движения точки
- Той же механической системы.
- Количество движения точки и импульс силы
- Ную геометрической сумме количеств движения всех точек данной системы,
- Взятого относительно какого-либо неподвижного центра, равна моменту действующей на точку силы относительно того же центра.
- ЛЕКЦИЯ 15. Принцип Даламбера
- Перемещение, которое допускается в данный момент времени наложенными на систему связями без их нарушения.
- Общие теоремы динамики при ударе
- Геометрической сумме моментов ударных импульсов, действующих на систему.
Похожие статьи вашей тематики
Количеством движения точки называется векторная величина, равная произведе-
| нию массы точки на ее скорость, т.е. mV.
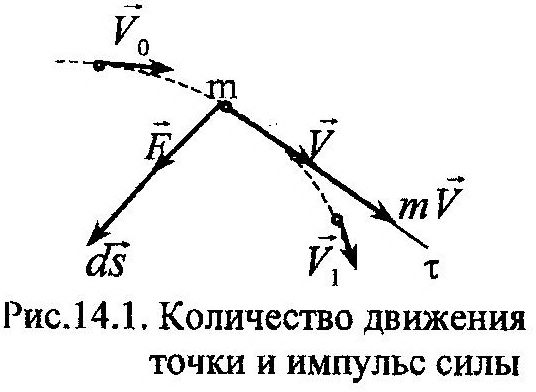
Вектор количества движения точки образуется на основе вектора ее скорости. Поэтому его направление совпадает с направлением скорости, т.е. касательной к траектории точки (рис. 14.1). Для характеристики действия силы на тело за некоторый промежуток времени используют понятие импульса силы. Введем вначале понятие элементарного импульса силы, dS, - векторной величи-
| ны, равной произведению вектора силы на элементарный промежуток времени, т.е.

Направление вектора импульса совпадает с направлением силы (рис. 14.1).
Следовательно, импульс силы за конечный промежуток времени определяется как определенный интеграл от элементарного импульса:

Ясно, что результат интегрирования зависит от вида функции силы. В частном случае,
| когда сила постоянна, имеем,
| 
| Импульс силы характеризует передачу телу механического движения за некоторый проме-жуток времени от других тел, где сила является количественной мерой этого взаимодей-ствия.
Теорема об изменении количества движения точки
| Для вывода используем основной закон динамики (11.1). Учитывая, что
| 
| и масса точки не зависит от времени, получим:

т.е., производная по времени от количества движения точки равна геометрической
Сумме сил, действующих на эту точку.
Выражение (14.9) представляет собой теорему об изменении количества движения точки,
записанную в векторной форме. При решении задач используют, как правило, скалярную форму записи данной теоремы в виде:

Выражение теоремы об изменении количества движения точки может быть представлено, также, в интегральном виде, если в (14.9) обе части умножить на dt и взять от полученного выражения интеграл (рис. 14.1), т.е.:

Под знаком суммы находится выражение импульса силы Fk за промежуток времени tO … tI.
Учитывая это, получим:

т.е., изменение количества движения точки за некоторый промежуток времени рав-
Но геометрической сумме импульсов всех действующих на точку сил за тот же промежуток времени.
В скалярной форме выражение данной теоремы можно получить если спроектировать обе части выражения (14.12) на координатные оси:
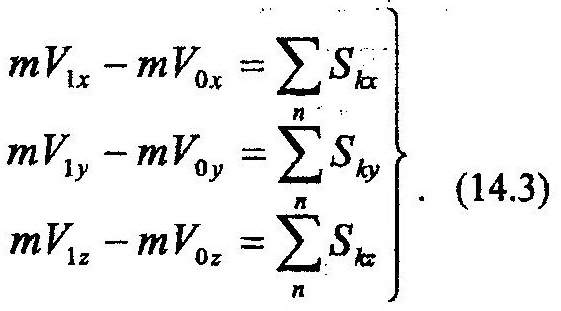
В случае движения точки по прямой для решения задачи достаточно воспользоваться одним из уравнений системы (14.13).
Количество движения механической системы
Количеством движения механической системы называют векторную величину, рав-
|