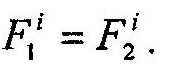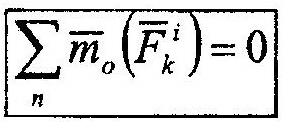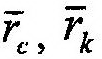Той же механической системы.

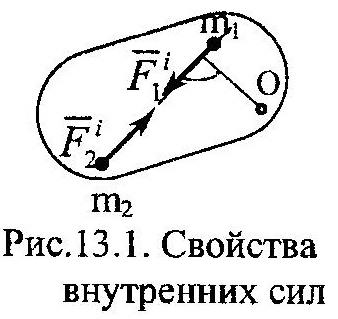
Внешними называются силы, действующие на точки или тела механической систе-

Мы со стороны других точек и тел, не входящих в данную систему.

Внутренние силы обозначаются верхним индексом «i», а внешние – «е». Такое деление сил никак не связано с другими классификациями. Это означает, что как внутренние, так и внешние силы могут одновременно являться активными или силами реакций, сосредоточенными или распределенными и т.д. Более того, в зависимости от постановки задачи одна и та же сила может быть как внешней, так и внутренней.

Внутренние силы обладают следующими свойствами.

Свойство 1: геометрическая сумма всех внутренних сил системы равняется нулю.

Свойство 2: сумма моментов всех внутренних сил системы относительно любого

Центра или оси равняется нулю.

Докажем эти свойства. Действительно, согласно третьего закона динамики между двумя произвольными точками механической системы действуют силы взаимодействия, равные между собой по модулю и направленные вдоль одной прямой в противоположные стороны (рис. 13.1), т.е.
	или		Нетрудно представить,
что любой внутренней силе всегда найдется такая же по вели-чине, но противоположная по знаку. Это означает, что сумма
	всех внутренних сил системы равняется 0, что и является первым свойством.

 

Докажем существование второго свойства. Определим моменты указанных на рисунке внутренних сил относительно произвольного центра «О», показанного на рисунке. Пусть кратчайшее расстояние от этого центра до линии действия сил равняется h. Тогда получим:

 

и их сумму:

т.к.

Ясно, что выражение, подобное (13.2), можно записать для любой пары внутренних сил, действующих на какие-либо другие две точки. Поэтому сумма моментов всех сил относи-

тельно любого центра будет равняться нулю,		что и сказано во втором
свойстве внутренних сил. Спроектировав обе части этого выражения, например, на ось х,
получим:

 

Из доказанных свойств не следует, однако, что внутренние силы взаимно уравновеши-ваются и не влияют на движение механической системы, т.к. эти силы приложены к раз-личным точкам или телам и способны вызвать их взаимное перемещение.

 

Центр масс механической системы

 

Центром масс механической системы называется точка, положение которой опреде-

Ляется следующими формулами

В векторном способе:

 

где		– масса механической системы; mk –
масса k -й точки системы;		– радиус-вектор цент-
ра масс и k -й точки системы.
В координатном способе:   Следует различать понятия центра тяжести и центра масс системы, положения которых в однородном поле тяжести совпадают.