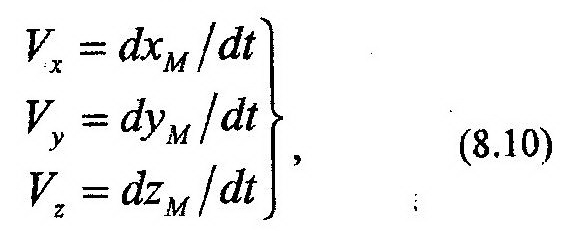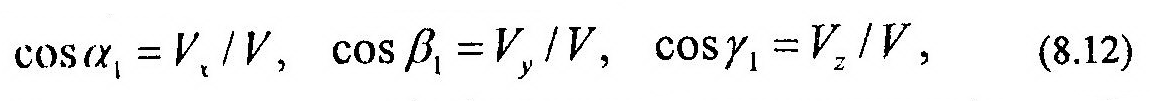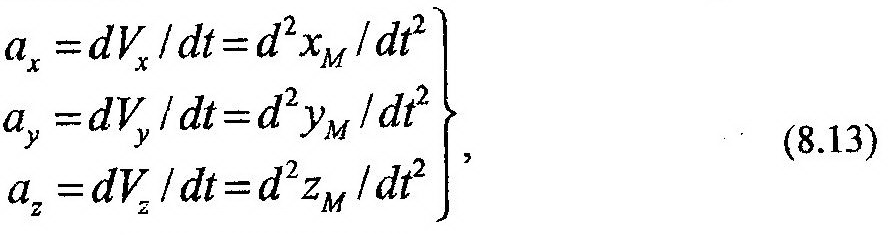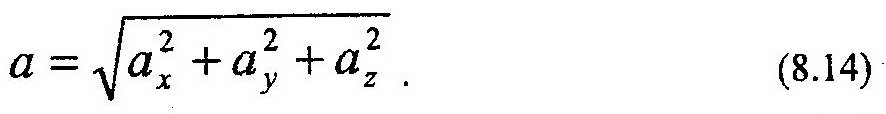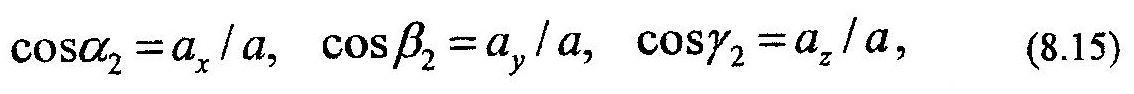Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 6. Ведение в кинематикуСодержание книги
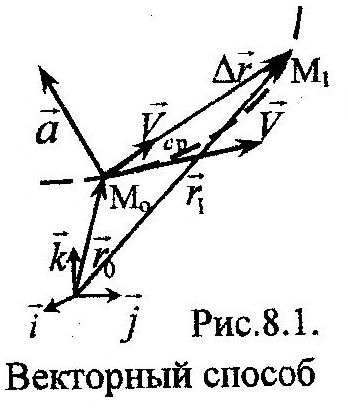
Поиск на нашем сайте Кинематикой называют раздел механики, в котором рассматривают движение тел и Точек без учета сил, приложенных к ним. 6.1. Способы задания движения точки Рассматривать движение тел или точек можно только относительно какой- либо системы отсчета – реального или условного тела, относительно которого определяют положение и движение других тел. Рассмотрим три, наиболее используемые при решении задач, системы отсчета и, соответствующие им, три способа задания движения точки. Их характеристика сводится к: а) описанию самой системы отсчета; б) определению положения точки в пространстве; в) указанию уравнений движения точки; г) установлению формул, по которым могут быть найдены кинематические характеристики движения точки. Векторный способ Данный способ используют, как правило, при выводе теорем и других теоретических положений. Его преимущество перед другими способами – компактность записи. В качестве системы отсчета в этом способе выступает центр О с тройкой единичных векторов – i, j, k (рис. 8.1). Положение в пространстве произвольной точки М определяется посредством радиуса-вектора, r. Таким образом, уравнением движения точки M будет однозначная функция радиуса-вектора от времени, t:
Сравнивая последние два определения, можно заключить, что траектория точки является одновременно годографом ее радиуса-вектора. Введем понятие средней скорости, Vср (рис. 8.1):
и истинной (мгновенной) скорости, V:
Направление V совпадает с касательной, к траектории точки (рис. 8.1). Ускорение точки – это векторная величина, характеризующая изменение скорости точки:
Естественный способ
ная зависимость между S и временем, t, представляет собой уравнение движения точки в естественном способе задания движения:
Скорость точки, направленная по оси t, определяется как:
Ускорение точки, а, находится в плоскости nt и может быть разложено на составляющие:
Физический смысл этого разложения заключается в следующем: линия действия касательной составляющей, аt, совпадает с линией действия вектора скорости, V, и отражает изменение только модуля скорости; нормальная составляющая ускорения, аn, характеризует изменение направления линии действия вектора скорости. Их численные значения могут быть найдены по следующим формулам:
Координатный способ Этот способ наиболее часто используют при решении задач. Системой отсчета является тройка взаимно перпендикулярных осей x, y, z (рис. 8.3). Положение точки М определяется ее координатами xМ, yМ, zМ. Уравнения движения точки представляют собой однозначные функции этих координат от
а ее модуль:
Направление вектора скорости в пространстве можно аналитически определить с помощью направляющих косинусов:
Ускорение точки М можно установить по его проекциям на координатные оси:
Направление вектора ускорения в пространстве определяется направляющими косинусами:
ЛЕКЦИЯ 7. ДВИЖЕНИЕ ТЕЛА
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-21; просмотров: 436; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |


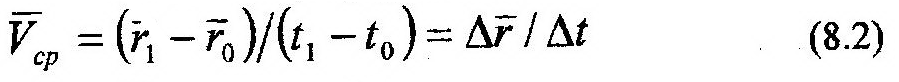
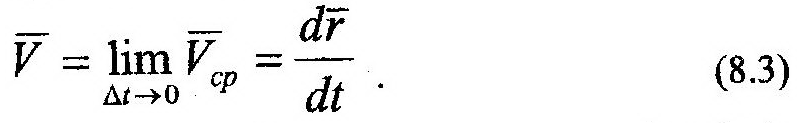





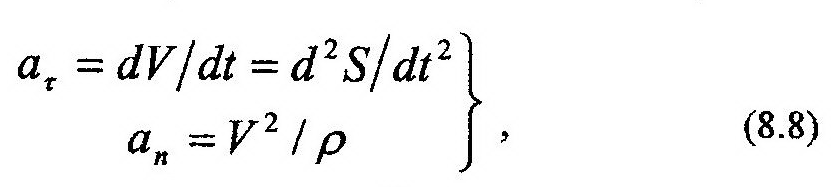
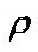
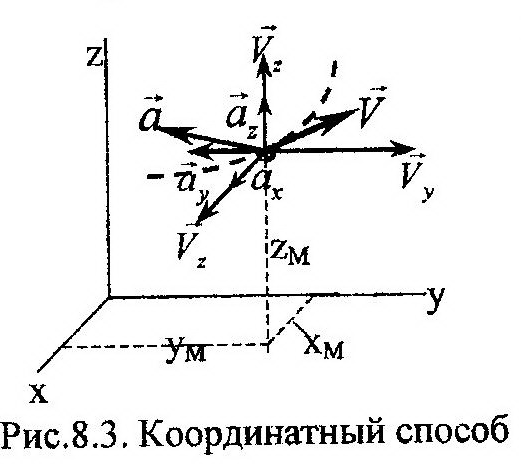
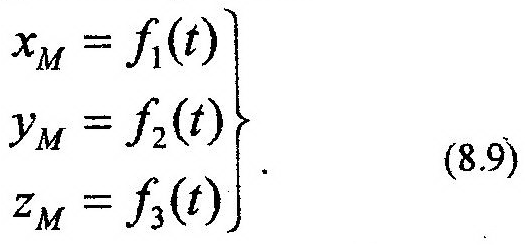 Составляющие скорости точки по осям равны:
Составляющие скорости точки по осям равны: