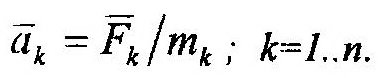Скорость своего движения под действием приложенных к нему сил.

Мерой инертности является масса тела (точки). В механике масса тела (точки), m, является величиной скалярной, постоянной и положительной. Единицей измерения массы в системе СИ является [ кг ]. Однако характер движения тела зависит не только от суммарного значения массы, но и от ее распределения по объему тела.

 

Законы механики

 

В основе классической механики лежат следующие законы, впервые изложенные И. Ньютоном в работе «Математические начала натуральной философии» (1687г.).

 

1. Закон инерции: изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные силы не заставят ее изменить это состояние.

Данный закон позволяет поделить все системы отсчета на инерциальные и неинер-циальные.

Инерциальными системами отсчета являются такие системы, где выполняется за-

кон инерции; в противном случае, системы отсчета являются неинерциальными.

 

2. Основной закон динамики: произведение массы материальной точки на ее ускорение, которое она получает под действием силы, равно модулю этой силы, и направление ускорения совпадает с направлением вектора силы.

Из этого закона видно, что мерой инертности точки является ее масса. Действительно, при действии на две точки одинаковыми силами ускорение той точки будет меньше, у которой масса больше. Следует заметить, что второй закон удобнее использовать в следующей форме записи:

где

– геометрическая сумма системы сходящихся сил.

Действительно, на точку одновременно действуют несколько сил, образуя систему сходящихся сил. Их равнодействующая F и представлена в правой части выражения ос-

новного закона динамики.   3. Закон равенства действия и противодействия: две материальные точки взаимодействуют друг с дру-гом с силами, равными по модулю и направленными вдоль одной линии действия, проходящей через эти точки, в противоположные стороны, т.е.:

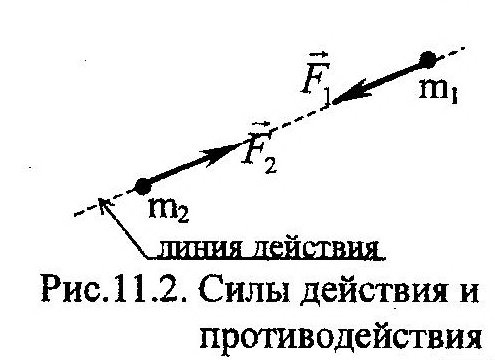
Здесь знак «-» указывает на противоположность направлений двух равных по модулю векторов, стоящих по обе стороны равенства. Следует заметить, что хотя геометрическая

сумма этих двух сил равна нулю,		однако, они не образуют уравнове-
шенную систему сил, т.к. приложены к разным точкам и вызывают их ускорения,
	(i=1;2).
	4. Закон независимости действия сил: материальная точка под действием системы сил получает ускорение, равное геометрической сумме ускорений, которые она имела бы при действии каждой силы в отдельности, т.е.:
где

Следует заметить, что для скорости точки аналогичная суперпозиция не имеет место.

 

 

Уравнения движения точки

 

В зависимости от способа описания движения точки для решения задач используют различные формы записи уравнений. Получим дифференциальные уравнения движения точки в координатной и естественной формах.