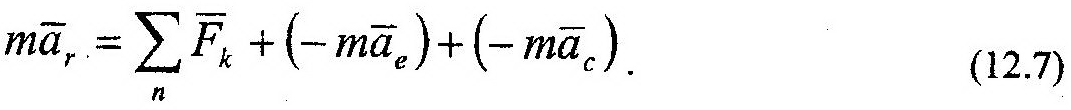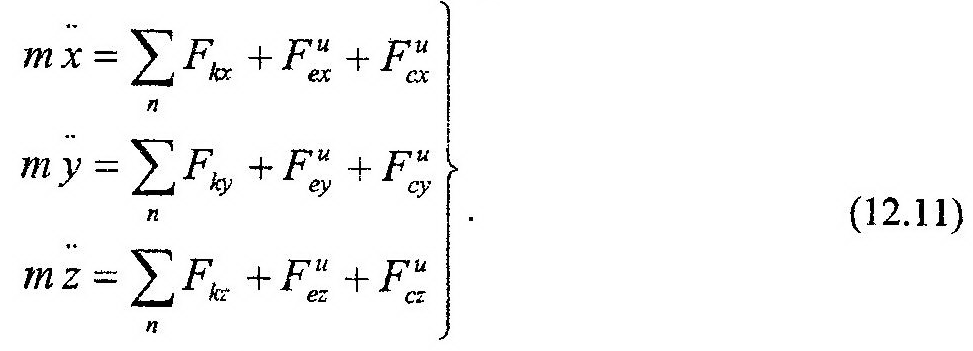Уравнение относительного движения точки

Приведенная выше информация относилась к задачам о движении точки в инерциальных системах отсчета, т.е. таких системах отсчета, где выполняется первый закон динамики (закон инерции).

Это означает, что в инерциальных системах отсчета при равенстве нулю правой части основного закона динамики (11.1) ускорение точки равно нулю. В противном случае, система отсчета является неинерциальной. В таких системах использовать основной закон или дифференциальные уравнения движения точки (12.2) не представляется возможным. Выведем уравнение, описывающее движение материальной точки в неинерциальной системе.

Пусть точка совершает сложное движение, представляющее собой сумму относительного и переносного движений. Тогда, ускорение точки относительно неподвижной системы от-

	счета, x1O1y1z1 (рис. 12.3), аа – абсолютное ускорение, равно:
где		– относительное, переносное и корио-
лисово ускорения соответственно. Подставим (12.5) в (11.1), получим: Решим это уравнение относительно ar – параметра, со-

ответствующего движению точки относительно подвижной системы отсчета:

 

Второе и третье слагаемые в (12.7) имеют размерность силы и называются переносной,

и кориолисовой,

силами инерции:

 

Согласно (12.8) направление действия сил инерции противоположно направлениям соответствующих векторов ускорений, а их модули равны:

 

В общем случае уравнение динамики относительного движения точки имеет следу-ющий вид:

 

Спроектировав (12.10) на координатные оси, получим:

 

Анализируя (12.10) и (12.11), можно сделать следующие выводы, что при рассмотрении движения материальной точки относительно подвижной системы отсчета:

- необходимо к ней, кроме фактически приложенных сил,		приложить дополни-
тельную переносную,		и кориолисову,		силы инерции;

- закон инерции (1-й закон динамики), в общем случае, выполняться не будет. Только в случае равномерного прямолинейного поступательного движения подвижной системы отсчета второе и третье слагаемые в правых частях (12.10) и (12.11) обращаются в нуль, и тогда закон инерции будет выполняться.

 

ЛЕКЦИЯ 12. МЕХАНИЧЕСКАЯ СИСТЕМА

Классификация сил

 

Механической системой называется такая совокупность материальных точек или тел, положение и движение которых взаимосвязаны.

Таким примером является Солнечная система, где каждое тело (планета, например) имеет свою определенную достаточно устойчивую траекторию движения. Применительно к механической системе силы делятся на внутренние и внешние.

Внутренними называются силы взаимодействия между точками или телами одной и