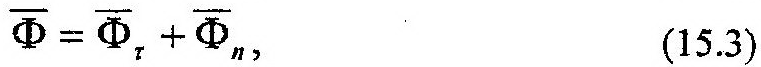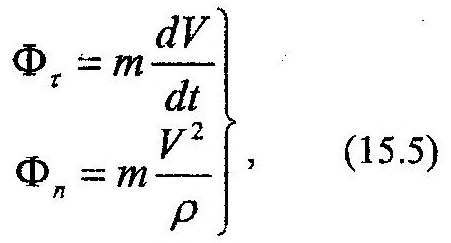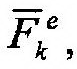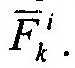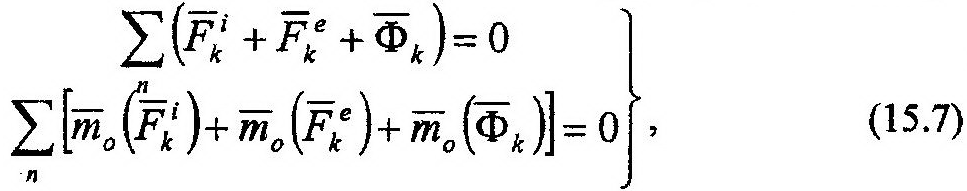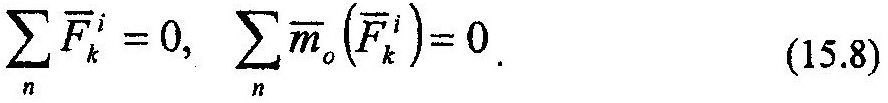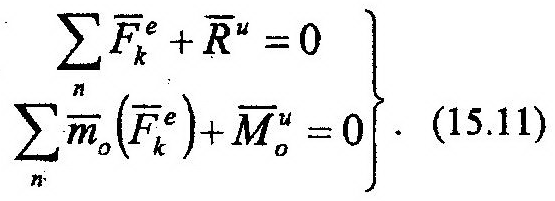Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ЛЕКЦИЯ 15. Принцип Даламбера
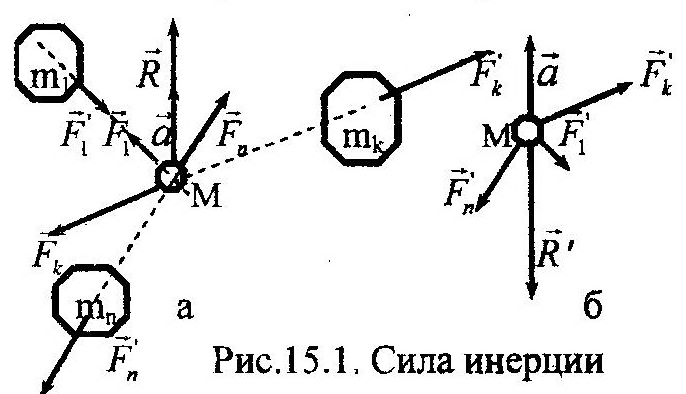
Область применения принципа Даламбера – это динамика несвободных механических систем. Даламбер предложил оригинальный метод решения задач динамики, позволяющий использовать достаточно простые уравнения статики. Он писал: «Данное правило приводит все задачи, относящиеся к движению тел, к более простым задачам о равновесии». В основу данного метода положены силы инерции. Введем это понятие. Силой инерции называют геометрическую сумму сил противодействия движущейся материальной частицы телам, сообщающим ей ускорение. Поясним это определение. На рис. 15.1 показана материальная частица М, взаимодей-ствующая с n материальными объектами. На рис. 15.1 показаны силы взаимодействия: без
щие на самом деле не на частицу, а на тела с массами m1, …, mn. Ясно, что равнодейст-вующая этой системы сходящихся сил противодействия, R’=ΣF’k, по модулю равна R и направлена противоположно ускорению, т.е.: R’=-ma. Данная сила и является силой инерции, о которой говорится в определении. В дальнейшем будем ее обозначать буквой Ф, т.е.:
В общем случае криволинейного движения точки ускорение представляет собой сумму двух составляющих:
Из (15.4) видно, что составляющие силы инерции направлены противоположно направлениям соответствующих составляющих ускорения точки. Модули составляющих силы инерции определяют по следующим формулам:
где ρ – радиус кривизны траектории точки.
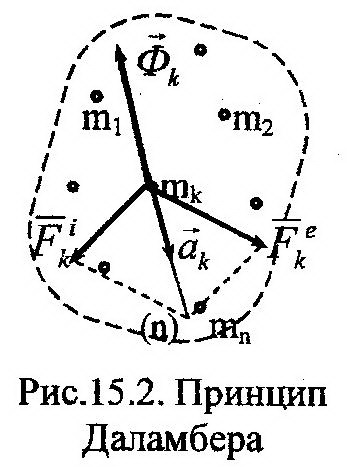
После определения силы инерции рассмотрим принцип Даламбера. Пусть дана механическая система, состоящая из n материальных точек (рис. 15.2). Возьмем одну из них. Все силы, действующие на k -ю точку, классифицируем по группам:
Выражение (15.6) отражает сущность принципа Даламбера, записанного для одной мате-риальной точки. Повторяя проделанные выше действия по отношению к каждой точке механической системы, можно записать систему n уравнений, подобных (15.6), что и будет являться математической записью принципа Даламбера применительно к механи-ческой системе. Таким образом, сформулируем принцип Даламбера для механической системы: Если к каждой точке механической системы в любой момент времени, кроме фактически действующих на нее внешних и внутренних сил, приложить соответствующую силу инерции, то вся система сил будет приведена в равновесное состояние и к ней можно будет применять все уравнения статики. Следует иметь в виду: - принцип Даламбера можно применять для динамических процессов, протекающих в инерциальных системах отсчета. Этого же требования, как отмечалось ранее, следует придерживаться и при применении законов динамики; - силы инерции, которые, согласно методики принципа Даламбера, необходимо прило- жить к точкам системы, на самом деле на них не действуют. Действительно, если бы они существовали, то вся совокупность сил, приложенных к каждой точке, находилась бы в равновесии, и отсутствовала бы сама постановка задачи динамики. Для равновесной системы сил можно записать следующие уравнения:
т.е. геометрическая сумма всех сил системы, включая и силы инерции, и геометрическая сумма моментов всех сил относительно произвольного центра равны нулю. Учитывая свойства внутренних сил системы:
выражения (15.7) можно заметно упростить. Вводя обозначения главного вектора
и главного момента
выражения (15.7) предстанут в виде:
Уравнения (15.11) являются прямым продолжением принципа Даламбера, но не содержат внутренних сил, что является их несомненным преимуществом. Их использование наиболее эффективно при исследовании динамики механических систем, состоящих из твердых тел.
ЛЕКЦИЯ 16. Принцип Лагранжа
Если принцип Даламбера позволяет привести систему в равновесное состояние, то принцип Лагранжа (принцип возможных перемещений) устанавливает в самом общем виде состояние равновесия. Таким образом, объектами его рассмотрения являются уравновешенные системы. Базовым понятием данного принципа является виртуальное (возможное) перемещение – это такое воображаемое достаточно малое
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-21; просмотров: 782; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.184.162 (0.01 с.) |