Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взятого относительно какого-либо неподвижного центра, равна моменту действующей на точку силы относительно того же центра.Содержание книги
Поиск на нашем сайте
Следует заметить, что в правой части (14.32) указан момент одной силы. В общем случае на точку действует система сил. Поэтому выражение (14.32) может быть переписано для общего случая, как:
Проектируя обе части выражения (14.33) на координатные оси, получим выражение той же теоремы в скалярной форме. Например, на х:
Движение точки под действием центральной силы
Центральной называется такая сила, линия действия которой проходит через дан- Ный центр на протяжении всего движения точки. Наглядным примером такой силы является притяжение Солнцем любой планеты, в какой бы точке свой траектории она не находилась. При этом линия действия силы все время будет проходить через Солнце. Рассмотрим эту задачу в общем виде. Пусть на точку М действует центральная сила F, линия действия которой пересекает центр О (рис. 14.5). По-
стольку два вектора, стоящие в левой части выражения (14.36) все время остаются в одной и той же плоскости (хОу – рис. 14.5). Это означает, что траектория точки будет являться плоской кривой. Постоянство модуля вектора-момента количества движения точки приводит к следующему:
Учитывая, что скорость точки V=ds/dt, а dS*h=2dσ (где dσ – элементарная площадь сектора, заштрихованного на рис. 14.5), получим: где dσ/dt – секторная скорость. Подводя итоги рассмотренной задачи, можно сделать общий вывод о том, что: Материальная точка под действием центральной силы движется по плоской кривой с постоянной секторной скоростью. Главный момент количеств движения Механической системы
Главным моментом количеств движения механической (кинетическим моментом) называется геометрическая сумма моментов количеств движения материальных точек данной системы:
Аналогично (14.40) определяются кинетические моменты системы относительно координатных осей:
Если количество движения системы, Q, характеризует поступательную составляющую движения механической системы, то кинетический момент, К, - ее угловое перемещение. Очевидно, что выражения (14.40) и (14.41) неудобны для вычисления кинетических моментов, поскольку они подразумевают длительный процесс суммирования. При вращательном движении тела можно предложить удобную форму вычисления данной характеристики. На рис. 14.6 представлено тело, совершающее вращательное движение относительно неподвижной оси z. Найдем Kz для данного случая, для чего запишем момент количества движения произвольной точки М относительно оси z. Получим:
Для достижения цели воспользуемся выражением (14.41). Подставив в него (14.42),
(14.18). Действительно, кинетический момент и количество движения являются динамическими характеристиками механической системы. Они определяются как произведение меры инертности на скорость. В случае расчета величины количества движения, характеризующей поступательную составляющую движения системы, используется масса и линейная скорость, а при определении кинетического момента – момент инерции и угловая скорость. Структура этих выражений следующая:
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-21; просмотров: 387; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.103.100 (0.005 с.) |




 или
или
 Полученный результат позволяет сделать следующие выводы. Поскольку вектор-момент количества движения точки не меняет свое направление в пространстве, по-
Полученный результат позволяет сделать следующие выводы. Поскольку вектор-момент количества движения точки не меняет свое направление в пространстве, по-






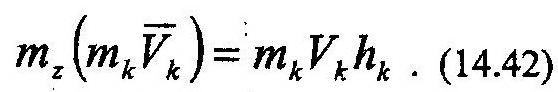
 или Kz=Izω (14.43)
или Kz=Izω (14.43)