Момент равнодействующей плоской ссс относительно любого центра, лежащего в той же плоскости, равен алгебраической сумме моментов слагаемых сил относительно того же центра.

Рассмотрим ССС (F1…Fn), линии действия которых пересекаются в точке А. Воспользуемся следствием 2-й аксиомы и приложим их в этой точке (рис. 2.7). Пусть сила R является равнодействующей данной системы сил, т.е.:

Соединим точку А с центром О и проведем ось О_х перпендикулярно отрезку ОА. Положительное направление оси зададим таким образом, чтобы знаки проекции любой силы на эту ось и ее момента относительно точки О совпадали. На основании свойства 3 момента силы, можно записать для произвольной силы F_k следующее:

но, с другой стороны, удвоенная площадь ΔОАВ может быть определена как:

Следовательно,

 

Спроектируем обе части (2.13) на ось х и умножим их на постоянную величину ОА, получим:

 

Сравнивая обе части (2.17) с (2.16), приходим к выводу, что:

 

что и требовалось доказать.

Формула (2.18) является математическим выражением теоремы Вариньона.

Следует заметить, что данную теорему можно использовать не только к системе сил, но и к любой системе векторов, о чем мы убедимся в следующих разделах.

 

Пара сил

Парой сил называется система двух равных по модулю параллельных и противоположно направленных сил, приложенных к АТТ.

Действие пары сил на тело сводится к его вращательному движению. На рис. 3.3. показана пара сил (F, F’). Из определения пары следует, что уравновесить ее никакой другой силой нельзя, т.к. F+ F’=0. Действие пары сил определяется: 1) величиной момента пары; 2) положением в пространстве ее плоскости действия; 3) направлением вращения пары.

Плоскостью действия пары называется плоскость, в которой находятся силы пары.

Моментом пары называется величина, равная взятому с соответствующим знаком произведению модуля силы пары на ее плечо, т.е.:

где d – плечо пары, равное кратчайшему расстоянию между линиями действия сил

пары (рис. 3.3).

 

Величина момента пары считается положительной, когда вращение пары направлено против часовой стрелки; в противном случае – отрицательной.

Рассмотрим теорему, указывающую на независимость величины момента пары от положения центра, относительно которого определяется сумма моментов сил.

Теорема: алгебраическая сумма моментов сил пары относительно произвольного

Центра, лежащего в ее плоскости действия, не зависит от положения центра и равна моменту пары.

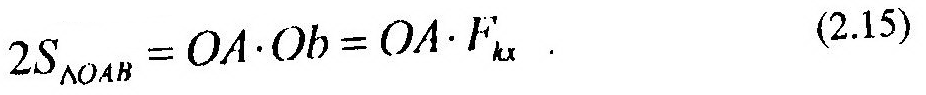
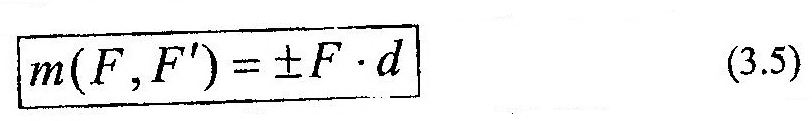
Пусть дана пара сил (F, F’)и произвольно выбранный центр О. Расстояние от центра до линий действия сил и плечо пары показано на рис. 3.4. Определим сумму моментов сил пары относительно точки О: что и требовалось доказать.