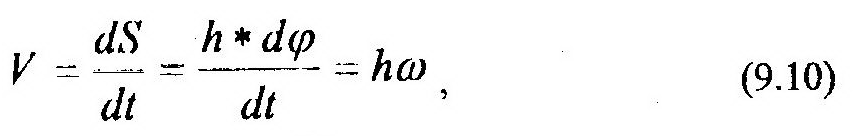Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поступательное движение тела
Поступательным называется такое движение тела, при котором любая его прямая остается параллельной самой себе. При поступательном движении точки тела могут описывать как прямолинейные, так и криволинейные траектории, что, и показано на рис. 9.1. Свойства поступательного движения: при поступательном движении все точки тела описывают одинаковые траектории и имеют в любой момент времени равные по
Видно, что годографы rА и rВ (или траектории точек А и В) отличаются только положением на постоянный вектор АВ. Неизменность модуля АВ вытекает из определения АТТ, а постоянство его направления – из определения поступательного движения тела. Взяв сначала первую, а затем вторую производную от обеих частей (9.1)
нулю, как производная от постоянной величины. Предыдущие члены этих выражений предоставляют собой скорости и ускорения точек А и В, соответственно. Учитывая сказанное, получим следующие зависимости:
что и указанно выше в свойствах поступательного движения тела. Отсюда следует, что поступательное движение тела определяется движением одной какой- либо его точки. Поэтому, уравнением поступательного движения тела будет выражение вида:
Вращательное движение тела Вращательным называется такое движение тела, при котором хотя бы две его точки Остаются неподвижными. На рис. 9.3 видно, что положение тела при его вращательном движении можно определить
I к подвижной плоскости II, жестко связанной с телом. Однозначная зависимость угловой координаты от времени является уравнением враща-тельного движения:
По формулам (9.6) и (9.7) видно, что определить эти кинематические характеристики тела можно как пределы отношений соответствующих приращений. Выражение для скорости какой-либо точки М тела (рис. 9.3) можно получить из формулы (8.6):
где h – кратчайшее расстояние от точки М до оси вращения. Выражение для касательной, ar, и нормальной, an, составляющих ускорения точки М могут быть найдены с помощью формул системы (8.8):
и
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-01-21; просмотров: 398; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.2.15 (0.005 с.) |



 Второе слагаемое в правой части выражения (9.2) равно
Второе слагаемое в правой части выражения (9.2) равно




 Основными кинематическими характеристиками вращательного движения тела являются его: угловая скорость – величина, характеризующая изменение угловой координаты
Основными кинематическими характеристиками вращательного движения тела являются его: угловая скорость – величина, характеризующая изменение угловой координаты
 и угловое ускорение – величина, определяющая изменение угловой скорости
и угловое ускорение – величина, определяющая изменение угловой скорости