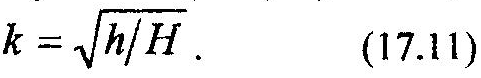Геометрической сумме моментов ударных импульсов, действующих на систему.

Закон сохранения кинетического момента будет иметь место, если:

то: K=const.

Следует отметить, что выражения (17.3) и (17.8), рассмотренных выше теорем, могут быть записаны в скалярной форме, если их спроектировать на какую-либо координатную ось. Аналогично и законы сохранения могут иметь место относительно только какой-либо одной оси.

2. Теорема об изменении кинетической энергии механической системы для решения задач в теории удара не применяется по следующим причинам:

- при ударе отсутствуют перемещения точек и, соответственно, работа сил не может быть найдена;

- вместо сил в теории удара используют их импульсы, что не позволяет использовать понятие работы силы.

 

Коэффициент восстановления

 

Величина ударного импульса зависит не только от масс и скоростей соударяющихся тел, но и от их механических свойств. Параметр, характеризующий эти свойства, называется

коэффициент восстановления – величина, равная при прямом ударе тела о неподвижную преграду отношению модулей скоростей, соответствующих концу и началу удара, т.е.:

Прямым называется такой удар, при котором скорость центра масс тела в начальный момент касания направлена по нормали; в противном случае удар называется косым.

Физические процессы, сопровождающие удар тел, довольно сложны и многообразны, но, в первом приближении, могут быть описаны следующей механической моделью. Рассмотрим прямой удар шара о неподвижную поверхность (рис. 17.1), как сумму двух стадий: 1) кинетическая энергия шара, равная в начале удара 0,5mV^2 (шар движется поступательно), убывает до нуля, переходя во внутреннюю потенциальную энергию деформированного тела;

2) происходит восстановление формы шара за счет внутренних упругих напряжений и приобретение точками тела в конце удара скорости U (обратный переход потенциальной энергии в кинетическую). Однако, полностью кинетическая энергия шара не восстанавливается, т.к. часть ее уходит на нагрев тела и его пластическое деформирование (0,5mU²<0,5mV²). Из этой модели видно, что коэффициент восстановления имеет следующий интервал возможных значений: 0≤k≤1. При k=1 удар считается абсолютно упругим; при k=0 – абсолютно неупругим. Согласно (17.9), в первом случае скорость тела после удара будет равна скорости до удара, т.е.: U=V (кинетическая энергия не расходуется на нагрев и пластическое деформирование); во втором случае удар заканчивается по завершению первой стадии выше рассмотренной модели удара, т.е.: U=0 (вся кинетическая энергия тратится на нагрев и пластическое деформирование тела). Очевидно, что крайние значения k для твердых тел практически не реализуемы, т.к. вторая стадия удара и рассеяние энергии всегда будет иметь место.

Коэффициент восстановления можно определить опытным путем следующим образом. Учитывая, что скорости в начале и в конце удара можно определить по формулам где h, H – расстояния шара от поверхности при его отскоке и в начальном положении соответственно (см. рис. 17.2).

Преобразуем выражение (17.9) с учетом (17.10), получим:

В выражение (17.11) входят величины, которые можно напрямую измерить, что позволяет контролировать точность определения k.