Фермой называется жесткая (неизменяемая) конструкция из прямолинейных стержней, соединенных на концах шарнирами.

Ферма называется плоской, если её стержни расположены в одной плоскости, в противном случае – пространственной. Места соединения стержней фермы называются узлами.

В данных методических указаниях рассмотрены только плоские фермы и аналитические методы их расчеты.

Для того, чтобы ферма обладала жесткостью, число узлов k и число стержней n должны быть связаны соотношением

 

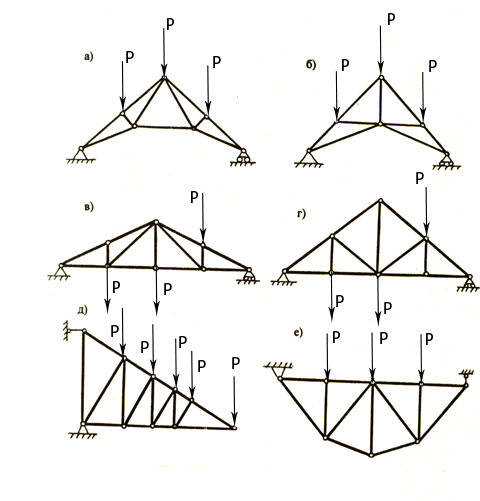
k = 2n – 3 (1)

Если k < 2n-3, то конструкция не будет обладать жесткостью, т.е. фермой не будет. Если k > 2n-3, то ферма имеет лишние стержни.

Плоская ферма будет статически определимой, если выполняется условие жесткости (1). В этом случае усилия в стержнях можно определить методами статики твердого тела. На рис.3 показаны различные виды статически определимых плоских ферм. Если же k > 2n-3, то усилия в стержнях посредством только одних уравнений статики твердого тела определить нельзя и ферма будет статически неопределимой.

Расчет статически определимой фермы сводится к определению опорных реакций и усилий в её стержнях.

 

 

Рис.1. Различные виды плоских ферм:

 

 

а – ферма Полонсо;

б – немецкая ферма;

в – английская ферма;

г – американская ферма;

д – бельгийская ферма (раскосы перпендикулярны

к стержням верхнего пояса);

е – параболическая ферма (узлы нижнего пояса

расположены по параболе)

 

Опорные реакции можно найти методами статики, рассматривая ферму как твердое тело, на которое действуют заданные силы. Заданные силы и опорные реакции по отношению к ферме являются внешними силами.

 

 

Расчет усилий в стержнях становится весьма простым, если под действием внешних сил стержни фермы подвергаются только продольным усилиям, т.е. стержни работают только на растяжение или сжатие. Для этого должны иметь место следующие допущения:

1) стержни фермы должны быть соединены шарнирами без трения (такие шарниры называются идеальными);

2) все внешние силы к ферме прикладываются только в узлах;

3) весом стержней пренебрегают (по сравнению с внешними нагрузками) или распределяют вес стержней по узлам.

Определяют усилия в стержнях фермы, используя аналитические методы расчета, а именно, метод вырезания узлов и метод сечений (метод Риттера).

Метод вырезания узлов. Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Суть метода состоит в том, что вырезают узлы фермы и прикладывают к ним соответствующие внешние силы и реакции стержней. Эти силы образуют плоскую уравновешенную систему сходящихся сил, тогда для каждого узла имеем по два уравнения равновесия:

∑F_kx = 0; ∑F_ky = 0; (2)

 

Так как в начале расчета неизвестно, какие стержни фермы растянуты, и какие сжаты, то условно предполагают, что все стержни растянуты (реакции стержней направлены от узлов).

Если в результате вычислений получают ответ со знаком минус, то соответствующий стержень сжат. Найденные реакции стержней равны по величине внутренним усилиям в стержнях.

Последовательность рассмотрения узлов определяется так, чтобы число неизвестных сил, приложенных к узлу, не превышало двух. Тогда эти неизвестные определяются из уравнений (2).

Метод сечений (метод Риттера). Этим методом удобно пользоваться для определения усилий в отдельных стержнях фермы независимо от остальных. Идея метода состоит в том, что ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в одном из них) требуется определить усилия и рассматривают равновесие одной из этих частей. Действие отброшенной части нужно заменить силами, направляя их вдоль разрезанных стержней от узлов, считая стержни растянутыми. Затем для выбранной части фермы составляют три уравнения равновесия, в которые войдут три неизвестных усилия. Если в сечении нет параллельных стержней, то эти уравнения удобно записать в виде равенства нулю суммы моментов всех сил, действующих на оставшуюся часть фермы, относительно трех центров. Эти центры называют точками Риттера - это точки, в которых попарно пересекаются рассеченные стержни (или их продолжения). В этом случае уравнение моментов для каждого центра будет содержать только одно неизвестное усилие в том стержне, направление которого через этот центр не проходит.

Если в сечении два из трех стержней параллельны, то одна из точек Риттера уходит в бесконечность, тогда для определения усилия в непараллельном стержне нужно взять сумму проекций всех сил на направление, перпендикулярное параллельным стержням.

КИНЕМАТИКА