
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение интерполяции для решения уравненийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Интерполяция применяется для решения уравнений вида
Если в области корня уравнения (2.17) вычислить его левую часть n +1 точке и результаты поместить в табл. 2.1, то для определения корня можно поменять местами столбцы таблицы и с помощью одного из алгоритмов интерполяции найти значение аргумента х, при котором функция f(x) принимает значение Значение корня, найденное с помощью обратной интерполяции, будет приближенным за счет погрешности интерполяции. Для его уточнения необходимо организовать итерационный процесс, на каждом шаге которого узел, где величина
где хк — приближение к корню на k-й итерации; Обычно при решении уравнений методом обратной интерполяции выбирают фиксированное и сравнительно небольшое количество узлов. Если выбрать два узла, то получим алгоритм, полностью совпадающий с методом секущих. Рассмотрим случай трех узлов. При этом левая часть решаемого уравнения аппроксимируется полиномом второй степени и алгоритм называется методом парабол. Итак, пусть известны три начальных приближения к корню
Для простоты полагаем Введем обозначение
где
Из двух корней последнего уравнения относительно z выбираем минимальный по модулю, затем вычислим величины.
На следующей итерации полином строим по точкам
Основное время при решении уравнений методом парабол затрачивается на вычисление левой части уравнений f(x). Можно составить программу таким образом, что функция f(x) вычисляется три раза только на первой итерации, а на последующей итерации лишь один раз, информация о значении функции в двух других узлах сохраняется от предыдущей итерации.
Интерполяция сплайнами Полиномиальная интерполяция не всегда дает удовлетворительные результаты при аппроксимации зависимостей. Так, например, при представлении полиномами резонансных кривых колебательных систем большая погрешность возникает на концах ("крыльях") этих кривых. Несмотря на выполнение условий Лагранжа в узлах, интерполяционная функция может иметь значительное отклонение от аппроксимируемой кривой между узлами. При этом повышение степени интерполяционного полинома приводит не к уменьшению, а к увеличению погрешности. Возникает так называемое явление волнистости [4]. Для проведения гладких кривых через узловые значения функции чертежники используют упругую металлическую линейку, совмещая ее с узловыми точками. Математическая теория подобной аппроксимации развита за последние тридцать лет [5, 6] и называется теорией сплайн-функций. Разработано и обширное программное обеспечение для применения сплайнов в различных областях науки и техники [7, 1]. Рассмотрим один из наиболее распространенных вариантов интерполяции кубическими сплайнами. Используя законы упругости, можно установить, что недеформируемая линейка между соседними узлами проходит по линии, удовлетворяющей уравнению
Функцию Если в качестве функции
где В отличие от полиномиальной интерполяции, когда вся аппроксимируемая зависимость описывается одним полиномом, при сплайно-вой интерполяции на каждом интервале Коэффициенты сплайнов определяются из условий сшивания соседних сплайнов в узловых точках: 1) Равенство значений сплайнов
2) Непрерывность первой и второй производных от сплайнов в узлах
Кроме перечисленных условий необходимо задать условия на концах, т.е. в точках
Для улучшения гладкости аппроксимирующей кривой используют и другие граничные условия. Например, строят так называемые нагруженные сплайны, которые в механической модели соответствуют подвешиванию грузов к металлической линейке на ее концах. Получим алгоритм определения коэффициентов кубических сплайнов из условий (2.20 — 2.24). Условия (2.20) в узлах xi-1 и x i после подстановки i -гo сплайна принимают вид ai = ƒi-1 , (2.25) ai + bi hi + cihi2 + dihi3 = ƒi ,(2.26) где hi = xi — xi- 1, 1 ≤ i ≤ n. Продифференцируем дважды сплайн (2.19) по переменной x: φ′i(x) = bi + 2ci (x— xi-1) + 3di (x— xi-1)2, (2.27) φ″i(x) = 2ci + 6di (x— xi-1). (2.28) Из условий непрерывности производных (2.21) и (2.22) при переходе в точке xiот i-го к (i1)сплайну с учетом выражений (2.27) и (2.28) получим следующие соотношения: bi + 2ci hi + 3dihi2 = bi+1 ,(2.29) ci + 3dihi = ci + 1. (2.30) И, наконец, из граничных условий (2.23) и (2.24) на основании выражения для второй производной (2.28) получим, что c1 = 0, (2.31) cn + 3dn hn = 0. (2.32) Соотношения (2.25), (2.26), (2.29) — (2.32) представляют собой полную систему линейных алгебраических уравнений относительно коэффициентов сплайнов ai, bi, ci и di. Но прежде чем решать эту систему, выгодно преобразовать ее так, чтобы неизвестными была только одна группа коэффициентов ci. Из уравнений (2.30) коэффициенты diвыразим через коэффициенты ci: ci+1 —c i di = ————. (2.33) 3 hi Объединяя уравнения (2.25) и (2.26) с уравнением (2.33), представим коэффициенты biтакже через коэффициенты ci: f i — f i-1(c i+1 + 2c i)h bi = ———— - —————. (2.34) hi 3 После подстановки выражений (2.33) и (2.34) в соотношение (2.29) получим уравнение, в которое входят только неизвестные коэффициенты ci. Для симметричности записи в полученном уравнении уменьшим значение индекса i на единицу: hi-1 ci-1+2(hi-1+hi)ci + hici+1 = 3 где 2≤ i ≤ n. При i = n, учитывая условие свободного конца сплайна, в уравнений (2.35) следует положить cn+1 = 0. (2.36) Таким образом, п — 1 уравнение вида (2.35) вместе с условиями (2.31) и (2.36) образует систему линейных алгебраических уравнений для определения коэффициентов ci. Коэффициенты d i и b i вычисляются после нахождения ci по формулам (2.33) и (2.34), коэффициенты ai равны значениям аппроксимируемой функции в узлах в соответствии с формулой (2.25). В каждое из уравнений типа (2.35) входит только три неизвестных с последовательными значениями индексов ci-1, ci, ci+1. Следовательно, матрица системы линейных алгебраических уравнений относительно ci является трехдиагональной, т.е. имеет отличные от нуля элементы только на главной и двух примыкающих к ней диагоналях. Для решения систем с трехдиагональной матрицей наиболее эффективно применять так называемый метод прогонки, являющийся частным случаем метода Гаусса. Рассмотрим алгоритм метода прогонки применительно к решаемой задаче. Для сокращения записи уравнение (2.35) представим в виде
hi-1 ci-1+si ci + hici+1 = ri, (2.37) где si = 2 (hi-1 - hi ), ri = 3 Так же, как и метод Гаусса, метод прогонки разделяется на два этапа — прямой и обратный ходы. В процессе прямого хода метода прогонки вычисляют значения коэффициентов линейной связи каждого предыдущего неизвестного ci с последующим ci+1. Из уравнения (2.37) при i = 2 с учетом граничного условия (2.31) установим связь коэффициента с2 с коэффициентом с3:
c2 = k2 - l2с3, (2.39) где k2 и l2 — прогоночные коэффициенты,
. r 2 h2 k2 = —, l2 = —. S 2 S2 Затем, подставляя выражение (2.39) в уравнение (2.37) при i = 3, получим линейную связь коэффициента с3 с коэффициентом с4: c3 = k3 - l3с4, Поступая аналогичным образом для любых соседних коэффициентов с номерами i и i + 1, можно установить линейную связь в виде ci = ki - liсi+1 (2.40) В процессе выполнения прямого хода метода прогонки необходимо вычислить значения всех прогоночных коэффициентов k i и li, для которых получим рекуррентные соотношения. Подставим формулу связи (i -1)-го и i -го коэффициентов ci-1 = ki-1 - li-1сi в уравнение (2.37), в результате получим ri - hi-1ki-1hi ci = ――――― - ————— ci+1. si - hi-1li-1 si - hi-1 li-1 Сравнение последнего соотношения с формулой (2.40) позволяет записать рекуррентные соотношения для определения прогоночных коэффициентов ki и li: ri - hi-1ki-1hi ki = ――――――, li = ——————. (2.41) si - hi-1li-1 si - hi-1 - li-1
Учитывая граничное условие (2.31) и соотношение c1 = k1 - l1с2, а также полагая c2 ≠0, задаем начальные коэффициенты k1 = 0 и l1 = 0. Затем по формуле (2.41) вычислим все п пар прогоночных коэффициентов k i и li.. На основании соотношения cn = kn - l ncn+1 и граничного условия (2.36) получим, что cn = kn. (2.42) далее последовательно применим формулу (2.40) при i = n — 1, n — 2,...., 2 и вычислим значения искомых величин cn-1, cn-2,…, c2 . Эта процедура называется обратным ходом метода прогонки. Метод прогонки применяют не только для решения задач сплайн-интерполяции. Он широко используется и при численном интегрировании граничных задач для линейных дифференциальных уравнений методом конечных разностей. После определения всех коэффициентов сi другие коэффициенты сплайна вычисляются по формулам (2.25), (2.33) и (2.34). Аппроксимирующую функцию φ(x) можно рассчитать с помощью соотношения (2.19) в любой точке x на интервале [ х0, хn ]. Глава 3 Метод наименьших квадратов Общие положения Если набор экспериментальных данных получен со значительной погрешностью, то не имеет смысла использовать интерполяцию полиномами Лагранжа и сплайнами для обработки результатов. В этом случае необходимо провести аппроксимирующую кривую, которая не проходит через экспериментальные точки, но в то же время отражает исследуемую зависимость, сглаживает возможные выбросы за счет погрешности эксперимента.
Обозначим узлы исходной таблицы данных через x j, где 0 ≤ j ≤ n — номер узла. Считаем известными значения экспериментальных данных в узловых точках ƒ(xj) = ƒj. Введем непрерывную функцию φ (х) для аппроксимации дискретной зависимости f(x j). В узлах функции φ (х) и f (x)будут отличаться на величину ε j = φ (x j) — - f(xj). Отклонения ε j могут принимать положительные и отрицательные значения. Чтобы не учитывать знаки, возведем каждое отклонение в квадрат и просуммируем квадраты отклонений по всем узлам: n n Q = ∑ ε j ² = ∑[φ(x j) - ƒ(x j)]² (3.1) j=0 j=0 Метод построения аппроксимирующей функции φ (х)из условия минимума величины Qполучил название метода наименьших квадратов (МНК). Наиболее распространен способ выбора функции φ (х)в виде линейной комбинации φ (х) = c0 φ 0 (x)+ c1 φ 1 (x) +... + cm φ m(x), (3.2) φ 0 (х), φ 1 (x),..., φ m (х) — базисные функции; m ≤ n; c0(x), c1 (x),.. cm (x)- коэффициенты, определяемые при минимизации величины Q. Математически условия минимума квадратов отклонений Q запишем, приравнивая к нулю частные производные от Qпо коэффициентам 0 ≤ k ≤ m: n ∂ Q⁄∂ c0 = 2∑ [c0 φ 0 (x j) + c1 φ 1(x j) +…+ j=0 + cm φ m (x j) - ƒj] φ 0 (x j) = 0, n ∂ Q⁄∂ c1 = 2∑ [c0 φ 0 (xj)+c1φ1(xj) +…+ (3.3 ) j=0 + cm φ m (x j) - ƒj] φ 1 (x j) = 0, ……………………………………. n ∂ Q⁄∂ cm = 2∑ [c0 φ 0 (x j) + c1 φ 1(x j) +…+ j=0 + cm φ m (x j) - ƒj] φ m (x j) = 0, Из системы линейных алгебраических уравнений (3.3) определяются все коэффициенты сk. Система (3.3) называется системой нормальных уравнений. Матрица этой системы имеет следующий вид:
и называется матрицей Грамма. Элементы матрицы Грамма являются скалярными произведениями базисных функций: n (φ j, φ k) = ∑ φ j (x j) φ k(x j). (3.5) j=0
Расширенная матрица системы уравнений (3.5) получится добавлением справа к матрице Грамма столбца свободных членов
где скалярные произведения, являющиеся элементами столбца, определяются аналогично (3.5):
n (φ j, ƒ) = ∑ φ j (x j) ƒ j j=0 Отметим основные особенности матрицы Грамма, полезные при программной реализации алгоритмов МНК: 1) Матрица симметрична, т.е. a i j = a j i, что позволяет сократить объем вычислений при заполнении матрицы. 2) Матрица является положительно определенной, следовательно, при решении системы нормальных уравнений методом исключения Гаусса можно отказаться от процедуры выбора главного элемента. 3) Определитель матрицы будет отличен от нуля, если в качестве базиса выбраны линейно независимые функции φk (x), при этом система (3.3) имеет единственное решение При обработке экспериментальных данных, определенных с погрешностью е в каждой узловой точке, обычно начинают с аппроксимации функцией φk (x), представимой одной-двумя базисными функциями. После определения коэффициентов ckвычисляют величину Q по формуле(3.1). Если получится, что √Q > e, то необходимо расширить базис добавлением новых функций φk (x).Расширение базиса необходимо осуществлять до тех пор, пока не выполнится условие √Q ≈ e.
Выбор конкретных базисных функций зависит от свойств аппроксимируемой функции ƒ(x), таких как периодичность, экспоненциальный или логарифмический характер, свойства симметрии, наличие ас-симптотики и т.д.[8] Степенной базис Выберем базисные функции в виде последовательности степеней аргумента х, которые линейно независимы: φ0 (x) = х 0 = 1, φ1 (x) = х1 = х,..., φm (х) = хm. (3.8) В этом случае также, как и при интерполяции, мы будем аппроксимировать экспериментальную зависимость полиномом. Однако степень полинома m выбираем обычно m << n(при лагранжевой интерполяции m = n). Аппроксимирующая кривая в МНК не проходит через значения исходной функции в узлах, но проведена из условия наименьшего суммарного квадратичного отклонения. Экспериментальные данные "сглаживаются" с помощью функции φ(x). Если же выбрать m = n, то на основании единственности интерполяционного полинома получим функцию φ(x), совпадающую с каноническим интерполяционным полиномом степени n, аппроксимирующая кривая пройдет через все экспериментальные точки и величина Qбудет равна нулю. Последнее обстоятельство используется для отладки и тестирования программ, использующих МНК. Запишем расширенную матрицу системы нормальных уравнений для базиса (3.8):
Нетрудно видеть, что для формирования расширенной матрицы (3.9) достаточно вычислить элементы первой строки и двух последних столбцов, остальные элементы не являются "оригинальными" и заполняются с помощью циклического заполнения. Для решения систем уравнений с матрицей Грамма разработаны методы сингулярного разложения [9]. Если же m ≤ 4 ÷ 5, то такие системы можно решать и более простым методом исключения Гаусса.
|
||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.205.161 (0.017 с.) |

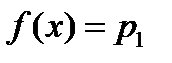 (2.17)
(2.17)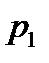 . Нахождение значений аргумента x по заданным значениям функции называется обратной интерполяцией.
. Нахождение значений аргумента x по заданным значениям функции называется обратной интерполяцией. принимает наибольшее значение, заменяется найденным приближением к корню. Критерием окончания итераций будет выполнение одного из условий
принимает наибольшее значение, заменяется найденным приближением к корню. Критерием окончания итераций будет выполнение одного из условий
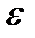 — заданная погрешность определения корня;
— заданная погрешность определения корня; 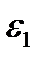 — предельная величина невязки.
— предельная величина невязки.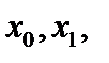 и
и  - Вычислим значения левой части уравнений в этих точках
- Вычислим значения левой части уравнений в этих точках 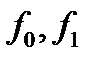 и
и 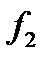 . По полученным данным построим интерполяционный полином Ньютона второй степени:
. По полученным данным построим интерполяционный полином Ньютона второй степени:
 , тогда, приравнивая полином к нулю, получим квадратное уравнение для определения очередного приближения к корню уравнения.
, тогда, приравнивая полином к нулю, получим квадратное уравнение для определения очередного приближения к корню уравнения.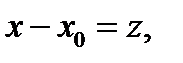 , тогда
, тогда  и квадратное уравнение принимает вид
и квадратное уравнение принимает вид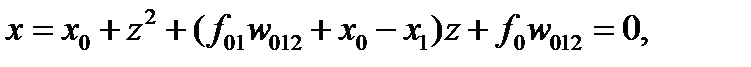
 -
-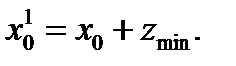
 Окончание итерационного процесса наступит, когда выполнится одно из условий
Окончание итерационного процесса наступит, когда выполнится одно из условий
 (2.18)
(2.18) и будем использовать для аппроксимации зависимости f(x), заданной в узлах
и будем использовать для аппроксимации зависимости f(x), заданной в узлах  ,...,хп значениями
,...,хп значениями  .
. выбрать полином, то в соответствии с уравнением (2.18) степень полинома должна быть не выше третьей. Этот полином называют кубическим сплайном, который на интервале
выбрать полином, то в соответствии с уравнением (2.18) степень полинома должна быть не выше третьей. Этот полином называют кубическим сплайном, который на интервале  записывают в виде
записывают в виде (2.19)
(2.19) и
и  — коэффициенты сплайна, определяемые из дополнительных условий; i = 1,2,..., п — номер сплайна.
— коэффициенты сплайна, определяемые из дополнительных условий; i = 1,2,..., п — номер сплайна. строится отдельный полином третьей степени(2.19) со своими коэффициентами.
строится отдельный полином третьей степени(2.19) со своими коэффициентами. и аппроксимируемой функции f(x) в узлах — условия Лагранжа
и аппроксимируемой функции f(x) в узлах — условия Лагранжа (2.20)
(2.20) (2.21)
(2.21) (2.22)
(2.22) и.
и.  В общем случае эти условия зависят от конкретной задачи. Часто используют условия свободных концов сплайнов. Если линейка не закреплена в точках вне интервала [
В общем случае эти условия зависят от конкретной задачи. Часто используют условия свободных концов сплайнов. Если линейка не закреплена в точках вне интервала [  (2.23)
(2.23) - (2.24)
- (2.24) (2.35)
(2.35) . (2.38)
. (2.38) (3.4)
(3.4) ,
, (3.9)
(3.9) 


