
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерполяция полиномом НьютонаСодержание книги
Поиск на нашем сайте
По данным табл. 2.1 построим интерполяционный полином степени п в виде, предложенном Ньютоном:
Равносильный вариант полинома можно записать при симметричной перенумерации узлов исходной таблицы 0 →n, 1→n-1, 2→n-2,…
Коэффициенты полиномов (2.6) и (2.7) определяются из условий Лагранжа
Полагаем
Затем полагаем
откуда находим коэффициент
который называется разделенной разностью первого порядка. Величина При х =
из условия Лагранжа (2.8) определяем искомый коэффициент
где
Величина Аналогичным образом при х =
где
Для коэффициента Ак методом математической индукции запишем следующее выражение:
Полученные результаты сведем в табл. 2.2. Таблица 2.2. Разделенные Разности
Для построения интерполяционного полинома Ньютона используются только диагональные элементы приведенной таблицы, остальные элементы являются промежуточными данными. Поэтому в программе, реализующей вычисление коэффициента полинома, разделенные разности для экономии памяти целесообразно размещать в массиве, где первоначально хранились значения функции f(x) в узлах. Этот массив будет частично обновляться при вычислении разделенных разностей очередного порядка. Так, при вычислении разностей первого порядка элемент остается неизменным (коэффициент Таким образом, после вычисления все коэффициенты полинома Ньютона будут размещены последовательно в массиве узловых значений функции f(x). Заметим, что добавление новых узлов в табл. 2.2 не изменит уже вычисленных коэффициентов, таблица будет дополнена новыми строками и столбцами разделенных разностей. Предлагаемая схема вычислений коэффициентов интерполяционного полинома Ньютона согласно табл. 2.2 обладает рядом преимуществ по сравнению с классической схемой [2, 1 ]. Во-первых, обеспечивается меньшая погрешность вычисления разделенных разностей при близко расположенных узлах за счет меньшего количества вычитаний близких чисел. Во-вторых, сокращается количество обращений к элементам массивов узлов и значений функции f(x), так как в формулах для разделенных разностей уменьшаемые в числителе и знаменателе остаются неизвестными для разности каждого порядка. В-третьих, аналитические выражения для коэффициентов полинома Ньютона получаются более простым способом. После определения коэффициентов полинома Ньютона вычисление его значений при конкретных аргументах х наиболее экономично проводить по схеме Горнера, получаемой путем последовательного вы несения за скобки множителей
В отличие от алгоритма вычисления полинома Лагранжа при интерполировании полиномом Ньютона удается разделить задачи определения коэффициентов и вычисления значений полинома при различных значениях аргумента х. Аналогичное разделение задач происходит при интерполяции каноническим полиномом (см. п. 2.1). Погрешность полиномиальной аппроксимации функции определяется соотношением [2]:
где
Оценку погрешности (2.15) можно провести до вычисления интерполяционного полинома, подобная оценка называется априорной. Однако обычно заранее нам не известны производные функции f(x), поэтому в вычислительной практике используют апостериорную оценку, т.е. оценку после вычислений. Апостериорная оценка основана на том, что в случае близкого расположения узлов разделенные разности являются приближенными значениями производных соответствующего порядка к, деленными на к!. Поэтому правая часть неравенства (2.15) приближенно совпадает по модулю с новым членом полинома Ньютона (2.6), появляющимся при добавлении (п + 1) -го узла. Таким образом, вычисление модуля каждого из членов суммы (2.6) позволяет установить, сколько узлов следует использовать для аппроксимации исходной функции f(x) с заданной погрешностью. Если узлы Xfc расположены равномерно с шагом h, то наименьшая погрешность будет в интервалах, примыкающих к центральному узлу, за счет минимальной величины произведения в правой части оценки (2.15). Особенно резко увеличивается погрешность при экстраполяции. В центральном интервале (при четном количестве узлов) получена следующая оценка погрешности [2, 1 ]:
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 204; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.126 (0.008 с.) |


 . (2.6)
. (2.6)
 (2.7)
(2.7) . (2.8)
. (2.8) , тогда в формуле (2.6) все слагаемые, кроме
, тогда в формуле (2.6) все слагаемые, кроме  , обращаются в нуль, следовательно,
, обращаются в нуль, следовательно,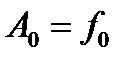 (2.9)
(2.9) , тогда по условию (2.8)
, тогда по условию (2.8) ,
, (2.10)
(2.10) близка к первой производной функции f(x) при малом расстоянии между узлами
близка к первой производной функции f(x) при малом расстоянии между узлами  и
и  .
. полином (2.6) принимает значение
полином (2.6) принимает значение
 , (2.11)
, (2.11)
 называется разделенной разностью второго порядка, которая при близком расположении
называется разделенной разностью второго порядка, которая при близком расположении 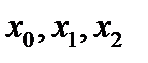 будет пропорциональна второй производной функции f(x).
будет пропорциональна второй производной функции f(x).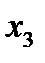 находим коэффициент полинома Ньютона
находим коэффициент полинома Ньютона (2.12)
(2.12)
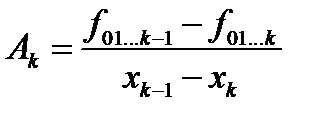 (2.13)
(2.13)

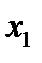












 (2.9)), элемент
(2.9)), элемент 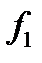 заменяется на
заменяется на  (коэффициент
(коэффициент 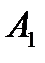 (2.10)),
(2.10)), 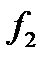 — на
— на 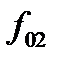 и т.д. При вычислении разделенных разностей второго порядка первые два элемента массива
и т.д. При вычислении разделенных разностей второго порядка первые два элемента массива  , где размещены коэффициенты
, где размещены коэффициенты  и
и  полинома, оставляем неизменными, остальные элементы заменяем разделенными разностями.
полинома, оставляем неизменными, остальные элементы заменяем разделенными разностями.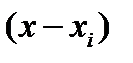 в формуле (2.6):
в формуле (2.6):
 (2.14)
(2.14) (2.15)
(2.15)
 . (2.16)
. (2.16)


