
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод квадратного корня (Холесского)Содержание книги
Поиск на нашем сайте
Если А — симметричная положительно определенная матрица, то существует и единственное разложение
где U — верхняя треугольная матрица. Выполним первый шаг факторизации, для чего запишем заданную матрицу А в блочной форме
,
где Теперь матрицу А можно факторизовать следующим образом:
где 0 — нулевой вектор-столбец,
Решение факторизованной системы осуществляется путем введения промежуточной векторной переменной Y
что анолгоично решению системы АХ=B. Эффективный алгоритм для такой схемы можно построить путем последовательного приравнивания элементов п-п — матриц А и U TU, стоящих в позициях (1,1), (1,2),..., (1, n), (2,2),..., (2, п),..., (n, n ). Окончательно алгоритм метода Холесского разложения матрицы на множители может быть записан следующим образом: 1) Для k= 1, 2, 3,..., п выполнить пп. 2 - 4. 2) Вычислить 3) Для j = k + 1, k + 2,..., n выполнить 4) Для i = k + 1,k + 2,...,n и j = k + 1, k + 2,..., п выполнить
5)Конец алгоритма. Элементы матрицы А изменили свои значения.
Можно модифицировать алгоритм так, чтобы элементы матрицы U были получены на месте элементов исходной матрицы А. Для этого необходимо заменить все переменные n на a. К недостатку метода можно отнести необходимость извлечения п квадратных корней, что является на некоторых типах ЭВМ достаточно медленной функцией. Метод исключения Холесского позволяет проверить положительную определенность матрицы. Если матрица не является положительно определенной, то в процессе исключения потребуется извлечь корень квадратный из отрицательного числа. Следует иметь в виду, что отрицательное подкоренное значение может также иметь место за счет погрешности, обусловленной накоплением ошибок округления для положительно определенных, но плохо обусловленных (почти вырожденных) матриц.
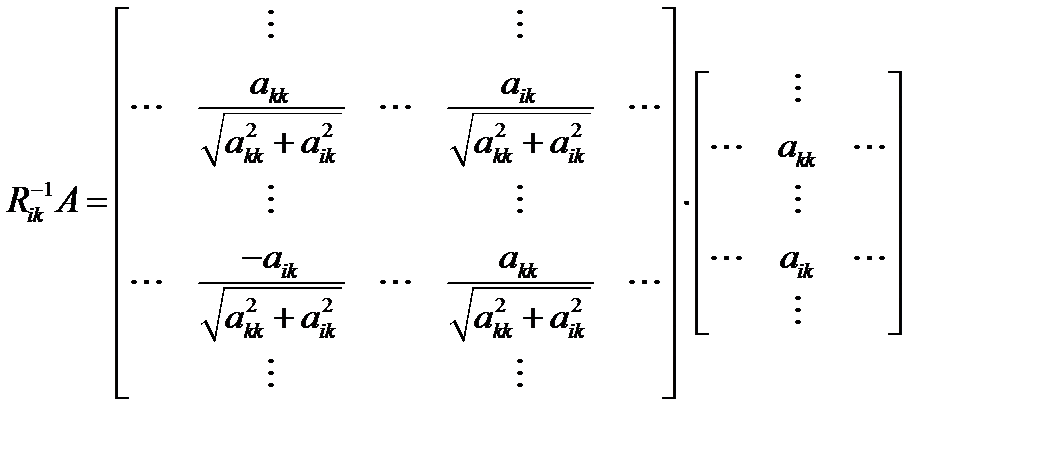
Метод вращений Матрицы вращений позволяют реализовать упорядоченное исключение переменных. Построим ортогональную матрицу вращений R21 так, чтобы при левом умножении матрицы, обратной к ней, на матрицу А она обращала в ноль элемент агь (исключение переменной x1 из второго уравнения) затем матрицу R31 для обращения в ноль а и так далее, пока не будут обращены в ноль поддиагональные элементы первого столбца матрицы А:
Выполним подобную последовательность операций для всех столбцов матрицы А. Получим факторизацию, на которой основан метод вращений (Гивенса):
Схема выполнения операций
Очевидно, что в результате обратится в ноль элемент Если необходимо решить одну систему уравнений с одной правой частью, то можно использовать следующий алгоритм решения: 1) Для k=1,2,3,…, n -1 выполнить пп. 2,3,4,5. 2) Для i=k+1, k+2,…,n выполнить пп. 3,4,5. 3) Вычислить элементы c и s матрицы вращения 4) Умножить матрицу A слева на a) положить
b) для j=k+1,k+2,…,n выполнить
5) Умножить Матрицу 6) Решить полученную систему уравнений в верхней треугольной форме методом обратной подстановки. 7) Конце алгоритма. Матрица A содержит в верхнем треугольнике матрицу U, вектор B – пересчитан.
Каждый шаг исключений переменной методом вращений из очередного k-го столбца системы уравнений состоит из нескольких малых шагов, на каждом из которых необходимо строит матрицу Следует обратить внимание на то, что в отличии от метода Гаусса пересчету на кадом малом шаге подлежат так же и элементы ведущей строки В силу ортогональности матриц вращения метод является численно более устойчивым, чем метод Гаусса, однако требует в три раза больше количества операции, причем (n-1)(n-1)/2 операций вызывают функции извлечения квадратного корня. Оценка общего числа необходимых операций приближенно равна Для решения систем с различными правыми частями и одинаковой матрицей A факторизацию выполняют один раз, при этом элементы s матриц вращения запоминают на месте обращаемых в ноль элементов матрицы A. При последующих расчетах элементы c могут быть рассчитаны по формуле
Итерационное уточнение При решении линейных алгебраических систем уравнений большой размерности накапливаются ошибки округления, полученное решение может неприемлемо отличатся от точного решения. В этом случае может быть применено итерационное уточнение, под которым понимают следующий процесс: 1) Решить исходную систему уравнений 2) Вычислить вектор невязок 3) Решить систему уравнений 4) Вычислить уточненное решение 5) Повотрить пп. 2,3,4,5. 6) Конец алгоритма.
Приведенный алгоритм вытекает из следующих соотношений
Т.к. AX=B, имеем:AX=R. Следует иметь в виду, что итерационное уточнение сходится, если для матрицы A максимальное собственное число Недостатком метода итерационного уточнения является необходимость сохранения исходной матрицы А для вычисления вектора невязок, а также увеличение количества операций. Однако в ряде случаев для обеспечения точности расчета итерационное уточнение может быть полезным.
|
||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 307; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.104.140 (0.008 с.) |

 ,
,
 ; В — симметричная подматрица размерности n -1;
; В — симметричная подматрица размерности n -1; 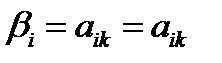 , i =k +1, k+2,..., п — вектор, построенный из элементов матрицы А; k — номер шага факторизации.
, i =k +1, k+2,..., п — вектор, построенный из элементов матрицы А; k — номер шага факторизации.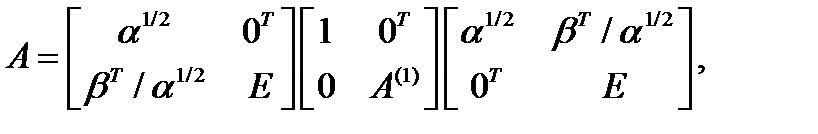
 - матрица порядка n-1,
- матрица порядка n-1,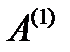 — симметричная и положительно определенная матрица, ее можно факторизовать таким же образом. Выполнив факторизацию п раз, получим А в виде 2п элементарных матриц
— симметричная и положительно определенная матрица, ее можно факторизовать таким же образом. Выполнив факторизацию п раз, получим А в виде 2п элементарных матриц  . Их произведение
. Их произведение .
. ,
, .
. .
.

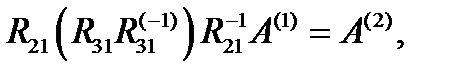 ……………………………………….
……………………………………….


 выглядит следующим образом
выглядит следующим образом .
.
 , для чего
, для чего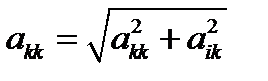

 .
. c индексами столбцов j, i, k.
c индексами столбцов j, i, k. .
. , если они не сохранены в специальных массивах данных. При решении нескольких систем с одной матрицей коэффициентов при неизвестных, но различными правыми частями общий объем вычислений сокращается.
, если они не сохранены в специальных массивах данных. При решении нескольких систем с одной матрицей коэффициентов при неизвестных, но различными правыми частями общий объем вычислений сокращается. .
. . Если все
. Если все  , где
, где  - желаемая точность, то расчет закончен и
- желаемая точность, то расчет закончен и  есть решение, иначе выполнить пп. 3,4,5.
есть решение, иначе выполнить пп. 3,4,5. относительно
относительно  - вектора итерационного уточнения.
- вектора итерационного уточнения. .
.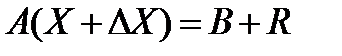 .
. сходимость может быть очень медленной, а при
сходимость может быть очень медленной, а при  процесс скорее всего расходится.
процесс скорее всего расходится.


