
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы наивысшей алгебраической точностиСодержание книги
Поиск на нашем сайте
Подынтегральную функцию f(x) так же, как и в методах Ньютона-Котеса, будем аппроксимировать полиномами различных степеней. Однако в отличие от методов Ньютона-Котеса узлы для построения интерполяционного полинома выберем из условия обеспечения минимальной погрешности интегрирования. Впервые задача построения квадратурных формул подобного типа была решена Гауссом для интегралов вида
а для интегралов
с произвольной весовой функцией р(х) — Кристоффелем [2]. Для того, чтобы узлы квадратурных формул не зависели от пределов интегрирования, линейными преобразованиями переменной х осуществляется переход к стандартным пределам [—1,1]:
где t — новая переменная. Тогда интеграл (4.42) принимает вид
Квадратурная формула Гаусса-Кристоффеля для интегралов типа (4.43) при п узлах содержит 2n параметров:
где Полином степени 2п - 1 также имеет 2n коэффициентов. Следовательно, можно так подобрать параметры Так, при п = 1 квадратура (4.46) будет точной для полиномов нулевой и первой степени. Этому требованию удовлетворяет метод средних прямоугольников, который является простейшим из методов Гаусса-Кристоффеля для весовой функции р{х) = 1. В случае двух узловых точек (п = 2) квадратура будет точной для полиномов не выше третьей степени (2n—1 = 3). Пусть подынтегральная функция интеграла (4.45) представима полиномом с коэффициентами
Тогда интеграл от полинома принимает значение
Интерполяционный полином Ньютона, совпадающий в узлах
где
Рис. 4.6. Метод Гаусса при n=2
Возьмем интеграл от полинома(4.49) и подставим в результат значения функции(4.47) в узлах t и
Сравнивая первые части выражений (4.48) и (4.49), получим систему двух уравнений относительно узлов
откуда получим
При таких узлах формула(4.46) с учетом соотношений (4.50) Принимает вид
где
Узлы Весовые коэффициенты С увеличением числа узлов их значениями остаются корни полиномов Лежандра степени n, а весовые коэффициенты
В таблице 4.2 приведены значения абсцисс и весов для квадратурных формул Гаусса методов порядка n.
Таблица 4.2. Абсциссы
Верхняя граница погрешности квадратурной формулы гаусса оценивается выражением [2]
которое позволяет сделать вывод об эффективности метода для интегрирования функции высокой гладкости.
Несобственные интегралы Известно несколько приемов вычисления разных типов несобственных интегралов [2,1]. Иногда удается заменой переменных перейти от интегралов с бесконечными пределами к интегралам с конечными пределами. Если подынтегральная функция после преобразования останется конечной на новом интервале, то для интегрирования можно использовать методы и программы, рассмотренные в предыдущих разделах. Довольно распространенным является способ образования верхнего предела интегрирования, при котором исходный несобственный интеграл разбивается на сумму двух интегралов
Затем оценивается аналитически, а иногда и численными методами модуль вторго интеграла, и при выполнении условия
в качестве приближенного значения несобственного интеграла выбирается величина интеграла в пределах [ 0,b ]. Для вычисления несобственных интегралов с бесконечными пределами применимы и квадратурные формулы Гаусса- Кристоффеля (4.46), узлы и веса которых определяются в зависимости от вида весовой функции Так, для интегралов в пределах [
где n – выбранное число узлов. Как правило, в программах используют заранее вычисленные узлы и веса квадратурных формул, задаваемых в виде констант. В справочниках [10,18] имеются достаточно подробные таблицы узлов и весов квадратурных формул Гаусса-Кристоффеля для различных видов функции p(x) и различных чисел n. Для интегралов в пределах Несобственные интегралы с конечными пределами интегрирования, но с подынтегральной функцией, обращающиеся в бесконечность в отдельных точках интервала [a,b], вычисляют методами аддитивного или мультипликативного выделения особенностей, а так же построения нестандартных квадратурных формул [2]. При аддитивном способе выделения особенности подынтегральную функцию представляют в виде суммы двух функций,
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 398; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.64.210 (0.008 с.) |

 (4.42)
(4.42) (4.43)
(4.43) (4.44)
(4.44) (4.45)
(4.45) (4.46)
(4.46) — весовые коэффициенты;
— весовые коэффициенты;  — узлы; R — погрешность квадратуры.
— узлы; R — погрешность квадратуры.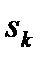
 (4.47)
(4.47) (4.48)
(4.48)
 со значениям подынтегральной функции
со значениям подынтегральной функции  и
и  , будет иметь первую степень (рис. 4.6):
, будет иметь первую степень (рис. 4.6): (4.49)
(4.49)

 :
: (4.50)
(4.50)
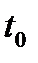 и
и 

 (4.51)
(4.51)
 (4.52)
(4.52)

 и
и  являются корнями полиномов Лежандра второй степени.
являются корнями полиномов Лежандра второй степени. равны единице.
равны единице. определяются через узлы по формуле [2]:
определяются через узлы по формуле [2]:
 и веса
и веса 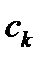 для квадратурной формулы Гаусса
для квадратурной формулы Гаусса



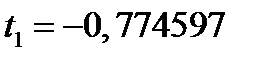














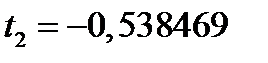




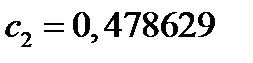



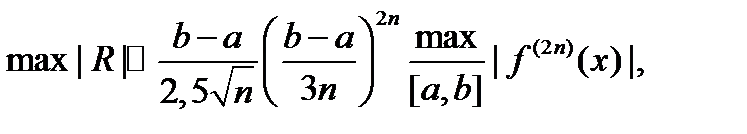 (4.53)
(4.53)


 , входящей под интеграл в форме произведения
, входящей под интеграл в форме произведения 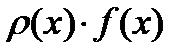 .
. ] при
] при  узлами квадратурной формулы (4.46) являются корни многочленов Лаггера
узлами квадратурной формулы (4.46) являются корни многочленов Лаггера  , а весовые коэффициенты
, а весовые коэффициенты  определяются через интеграл [2]:
определяются через интеграл [2]: (4.54)
(4.54)
 узлами квадратурной формулы (4.46) будут корни многочленов Эрмита
узлами квадратурной формулы (4.46) будут корни многочленов Эрмита  , а весовые коэффициенты определяются по формуле аналогичной (4.54), где интеграл необходимо взять в бесконечных пределах.
, а весовые коэффициенты определяются по формуле аналогичной (4.54), где интеграл необходимо взять в бесконечных пределах. где
где  ограниченная функция, а
ограниченная функция, а  - интегрируется аналитическими методами.. Для мультипликативного способа функция f(x) представляется в виде произведения
- интегрируется аналитическими методами.. Для мультипликативного способа функция f(x) представляется в виде произведения  , где
, где  ограниченна,
ограниченна,  положительная и интегрируемая на отрезке [a,b]. Тогда можно применить квадратурные формулы Гаусса-Кристоффеля, которые требуют вычисления в узлах функции
положительная и интегрируемая на отрезке [a,b]. Тогда можно применить квадратурные формулы Гаусса-Кристоффеля, которые требуют вычисления в узлах функции 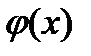 , при этом
, при этом  рассматривается как весовая функция.
рассматривается как весовая функция.


