
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типы задач для обыкновенных дифференциальных уравнений
Обыкновенные дифференциальные уравнения (ОДУ) широко используются для математического моделирования процессов и явлений в различных областях науки и техники. В дифференциальное уравнение n-го порядка в качестве известных входят функции y(x) и ее первые n производных по аргументу x:
Из теории ОДУ известно. Что уравнение (5.1) эквивалентно системе уравнений первого порядка
где k =1,…, n.
Уравнение (5.1.) и эквивалентная ему система (5.2) имеют бесконечное множество решений. Единственные решения выделяют с помощью дополнительных условий, которым должны удовлетворять искомые решения. В зависимости от вида таких условий рассматривают три типа задач, для которых доказано существование и единственность решений. Первый тип – это задачи Коши, или задачи с начальными условиями. Для таких задач кроме исходного решения (5.1) в некоторой точке
Для системы ОДУ типа (5.2) начальные условия задаются в виде
Ко второму типу задач относятся так называемые граничные, или краевые задачи, в которых дополнительные условия задаются в виде функциональных соотношений между искомыми решениями. Количество условий должно совпадать с порядком п системы. Если решение задачи определяется в интервале Третий тип задач для ОДУ - это задачи на собственные значения. Такие задачи отличаются тем, что кроме исходных функций у(х) и их производных в уравнения входят дополнительно т неизвестных параметров К численному решению ОДУ приходится обращаться, когда не удается построить аналитическое решение задачи через известные функции. Хотя для некоторых задач численные методы оказываются более эффективными даже при наличии аналитических решений.
Большинство методов решения ОДУ основано на задаче Коши, алгоритмы для которой рассматриваются в настоящей главе.
Метод Эйлера Систему ОДУ (5.2) часто удается представить в каноническом виде, в так называемом виде Коши:
где k = 1,2,..., n. При формулировке задачи Коши система (5.4) дополняется начальными условиями (5.3). Для простоты рассмотрим задачу Коши для одного уравнения типа (5.4), а затем полученные алгоритмы обобщим на систему п уравнений:
В окрестности точки х0 функцию у(х) разложим в ряд Тейлора
который можно применить для приближенного определения искомой функции у(х). В точке y(x0 + h) = y0 + hy'(x0) + O(h2), (5.7) где 0(h2) — бесконечно малая величина порядка h2. Заменим производную у'(
Теперь приближенное решение в точке
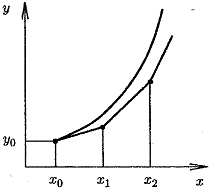
Рис.5.1.Метод Эйлера
Формула (5.8) может быть получена и из других соображений. Заменим производную в левой части уравнения (5.5) приближенным конечно-разностным отношением
Нетрудно видеть эквивалентность последнего выражения с алгоритмом Эйлера (5.8). На каждом шаге метода Эйлера решение у(х) определяется с погрешностью за счет отбрасывания членов ряда Тейлора, пропорциональных h в степени выше первой. Это означает, что метод Эйлера имеет второй порядок локальной погрешности. Глобальная погрешность, как показано в [19], имеет первый порядок и при постоянном шаге ft для оценки погрешности применима первая формула Рунге (4.14):
где Фомула (5.9) позволяет опытным путем определять шаг h, обеспечивающий требуемую точность решения у{х). Так же, как и при вычислении определенных интегралов, можно осуществить автоматическое изменение шага в процессе интегрирования дифференциального уравнения. Для уточнения решения применима вторая формула Рунге (4.15):
Формула Эйлера (5.8) обобщается для системы ОДУ, записанных в форме Коши (5.4) с начальными условиями (5.3)
Методы Рунге-Кутта Для уменьшения погрешности метода интегрирования ОДУ, использующего разложение искомого решения вряд Тейлора (5.6), необходимо учитывать большее количество членов ряда. Однако при этом возникает необходимость аппроксимации производных от правых частей ОДУ. Оснавная идея методов Рунге-Кутта заключается в том, что производные аппроксимируются через значения функции f(x, у) в точках на интервале Так, например, для второго порядка получено однопараметрическое семейство схем вида [2, 1]:
где 0 < £
Локальная погрешность схемы (5.12) имеет третий порядок, гло-* бальная — второй, т.е. решение ОДУ, полученное по этой схеме, равномерно сходится к точному решению с погрешностью 0(h2). Для параметра £ чаще всего используют значение £ = 0,5 и £ = 1. В первом случае формула (5.12) приобретает вид
геометрическая интерпретация которой представлена на рис.5.2,а [2, 1 ]. Вначале вычисляется приближенное решение ОДУ в точке х0+h по формуле Эйлера
Рис. 5.2. Метод Рунге-Кутта второго порядка: а) £ = О,5; б) £ = 1
С целью экономии памяти при программировании алгоритма (5.13), обобщенного для решения системы ОДУ, изменим его запись с учетом того, что
где к — номер решения для системы ОДУ. Теперь не придется держать в памяти ЭВМ массив начальных значений Во втором случае при £ = 1 от формулы (5.12) переходим к схеме
геометрический смысл которой отражает рис.5.2,6. Здесь при прогнозе определяется методом Эйлера решение в точке
а после вычисления наклона касательной к интегральной кривой в средней точке решение корректируется по этому наклону. Формула (5.15) обобщается для решения системы ОДУ аналогично схеме (5.14). По сравнению с программой метода Эйлера для сохранения начальных значений
Схему (5.14) можно получить из метода Эйлера с помощью первой и второй формул Рунге без использования общего соотношения (5.12) для методов второго порядка. Для построения вычислительных схем методов Рунге-Кутта других порядков в тейлоровском разложении искомого решения у(х) учи-, тываются члены, содержащие степени шага h до m включительно, где m — порядок схемы. После аппроксимации производных правой части ОДУ f(x, у) можно получить семейство схем Рунге-Кутта различных порядков [20, 21, 1], наиболее используемые из которых третьего и четвертого порядка приведены ниже. Они обобщаются для решения систем ОДУ, записанных в форме Коши. Одна из схем метода Рунге-Кутта третьего порядка имеет вид
где
Также используют другую схему
Схемы (5.16) и (5.17) на каждом шаге вычислений требуют нахождения правой части ОДУ в трех точках. Локальная погрешность схем имеет четвертый порядок, глобальной — третий. Схема метода Рунге-Кутта четвертого порядка имеет вид
Известна также схема метода Рунге-Кутта четвертого порядка:
Наиболее часто в вычислительной практике используют схему метода Рунге-Кутта четвертого порядка, поскольку она имеет рад преимуществ при программной реализации
Схемы (5.18) — (5.20) на каждом шаге требуют вычисления правой части ОДУ в четырех точках. Локальная погрешность этих схем имеет пятый порядок, глобальная — четвертый. Для удобства программной реализации, особенно в случае системы ОДУ, формулы (5.20) можно преобразовать к виду
i = 1,2,..., n — номер уравнения в системе ОДУ из п уравнений. Вычислительная схема метода Рунге-Кутта пятого порядка имеет вид
где
Схема (5.22) на каждом шаге требует вычисления правой части ОДУ в пяти точках. Локальная погрешность этих схем имеет шестой порядок, глобальная — пятый.
Метод Рунге-Кутта-Мерсона Мерсон предложил модификацию метода Рунге-Кутта четвертого порядка, позволяющую оценивать погрешность на каждом шаге и принимать решение об изменении шага. Схему Мерсона [22] с помощью эквивалентных преобразований приведем к виду, удобному для программирования:
Схема Мерсона требует на каждом шаге вычислять правую часть ОДУ в пяти точках, но за счет только одного дополнительного коэффициента ki по сравнению с классической схемой Рунге-Кутта на каждом шаге можно определить погрешность решения R по формуле
Для автоматического выбора шага интегрирования рекомендуется следующий критерий. Если абсолютное значение величины R, вычисленное по формуле (5.24), больше допустимой погрешности е, то шаг h уменьшается в два раза и вычисления по схеме (5.23) повторяются с точки 32|R | < Автоматический выбор шага позволяет значительно сократить время решения ОДУ. Схема (5.23) обобщается для решения системы ОДУ аналогично классической схеме Рунге-Кутта.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.184.237 (0.04 с.) |
 (5.1)
(5.1) (5.2)
(5.2)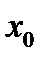 должны быть заданны начальные условия, т.е. значение функции y(x) и ее производных:
должны быть заданны начальные условия, т.е. значение функции y(x) и ее производных:
 (5.3)
(5.3)
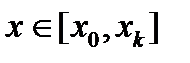 , то такие условия могут быть заданы как на границах, так и внутри интервала. Минимальный порядок ОДУ, для которых может быть сформулирована граничная задача, равен двум.
, то такие условия могут быть заданы как на границах, так и внутри интервала. Минимальный порядок ОДУ, для которых может быть сформулирована граничная задача, равен двум. , которые называют собственными значениями. Для единственности решения на интервале
, которые называют собственными значениями. Для единственности решения на интервале 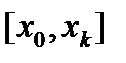 необходимо задать п + т граничных условий. В качестве примера можно назвать задачи определения собственных частот, коэффициентов диссипации, структуры электромагнитных полей и механических напряжений в колебательных системах, задачи нахождения фазовых коэффициентов затухания, распределения напряженности полей волновых процессов и т.д.
необходимо задать п + т граничных условий. В качестве примера можно назвать задачи определения собственных частот, коэффициентов диссипации, структуры электромагнитных полей и механических напряжений в колебательных системах, задачи нахождения фазовых коэффициентов затухания, распределения напряженности полей волновых процессов и т.д. (5.4)
(5.4)
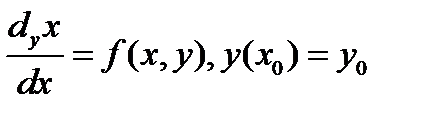 (5.5)
(5.5)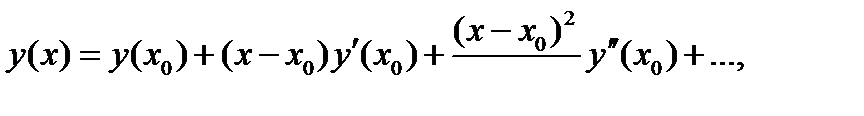 (5.6)
(5.6) при малых значениях h можно ограничиться двумя членами ряда (5.6), тогда
при малых значениях h можно ограничиться двумя членами ряда (5.6), тогда ), входящую в формулу (5.7), на правую часть уравнения (5.5):
), входящую в формулу (5.7), на правую часть уравнения (5.5): (5.8)
(5.8) =
=  + h можно вновь рассматривать как начальное условие, и по формуле (5.8) найти значение искомой функции в следующей точке х2 =
+ h можно вновь рассматривать как начальное условие, и по формуле (5.8) найти значение искомой функции в следующей точке х2 = 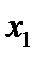 + h. В результате получен простейший алгоритм решения задачи Коши, который называется методом Эйлера или методом ломаных. Последнее название связано с геометрической интерпретацией процесса (рис. 5.1); искомую функцию у(х) мы заменяем ломаной линией, представляющей собой отрезки касательных к этой функции в узлах
+ h. В результате получен простейший алгоритм решения задачи Коши, который называется методом Эйлера или методом ломаных. Последнее название связано с геометрической интерпретацией процесса (рис. 5.1); искомую функцию у(х) мы заменяем ломаной линией, представляющей собой отрезки касательных к этой функции в узлах 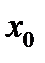 ,
,  ,...
,...
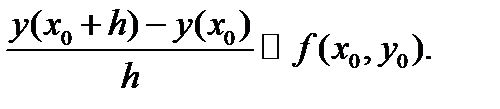

 — приближенное решение дифференциального уравнения в точке х, полученное с шагом h;
— приближенное решение дифференциального уравнения в точке х, полученное с шагом h; 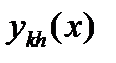 — приближенное решение того же уравнения с шагом kh; p — порядок метода.
— приближенное решение того же уравнения с шагом kh; p — порядок метода.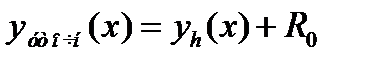 (5.10)
(5.10)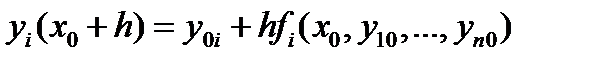 (5.11)
(5.11)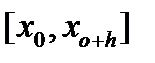 которые выбираются из условия наибольшей близости алгоритма к ряду Тейлора. В зависимости от старшей степени h, которой учитываются члены ряда, построены вычислительные схемы Рунге-Кутта разных порядков точности.
которые выбираются из условия наибольшей близости алгоритма к ряду Тейлора. В зависимости от старшей степени h, которой учитываются члены ряда, построены вычислительные схемы Рунге-Кутта разных порядков точности.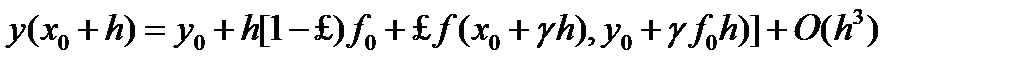 (5.12)
(5.12) 1 — свободный параметр,
1 — свободный параметр, .
.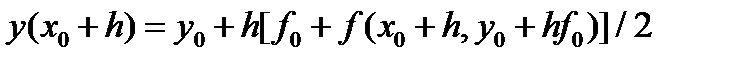 , (5.13)
, (5.13)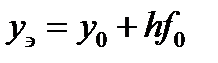 Затем определяется наклон интегральной кривой в найденной точке
Затем определяется наклон интегральной кривой в найденной точке 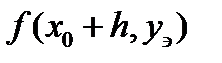 и после нахождения среднего наклона на шаге h находится уточненное значение
и после нахождения среднего наклона на шаге h находится уточненное значение 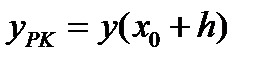 .. Схемы подобного типа называют "прогноз — коррекция", что подразумевает грубое вычисление решения по формуле низкого порядка, а затем уточнение с учетом полученной информации о поведении интегральной кривой.
.. Схемы подобного типа называют "прогноз — коррекция", что подразумевает грубое вычисление решения по формуле низкого порядка, а затем уточнение с учетом полученной информации о поведении интегральной кривой.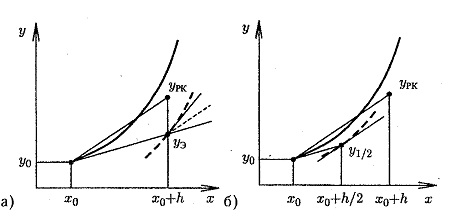
 :
: (5.14)
(5.14) , его можно не сохранять после вычисления значений эйлеровских приближений
, его можно не сохранять после вычисления значений эйлеровских приближений 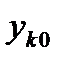 .Хотя по сравнению с методом Эйлера схема (5.14) требует дополнительного массива для запоминания значений
.Хотя по сравнению с методом Эйлера схема (5.14) требует дополнительного массива для запоминания значений 
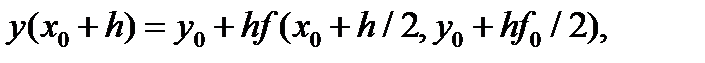 (5.15)
(5.15)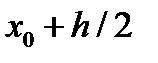
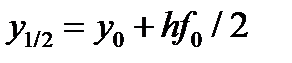 ,
,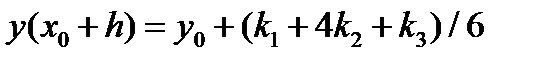 , (5.16)
, (5.16)
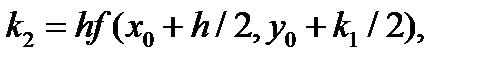
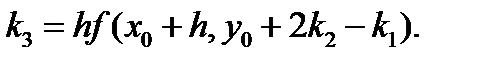 .
.
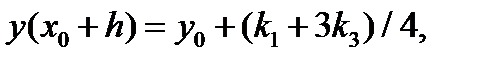 (5.17)
(5.17)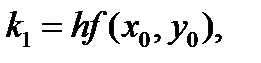

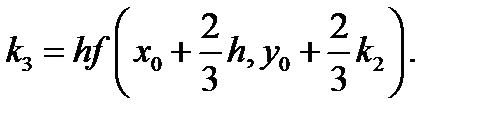
 , (5.18)
, (5.18)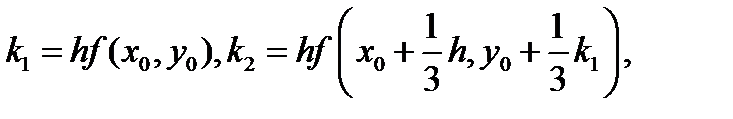
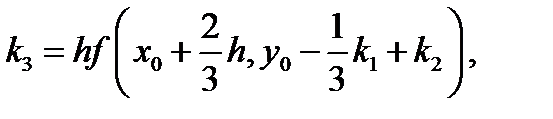

 (5.19)
(5.19)
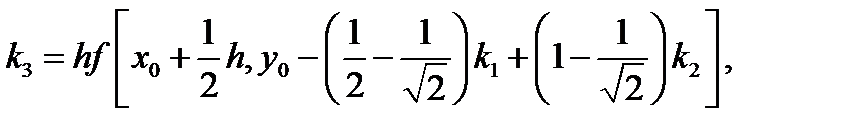
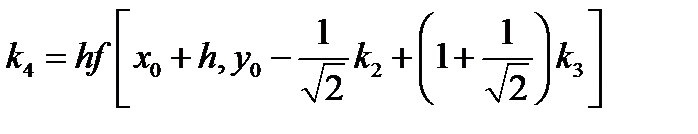 .
.
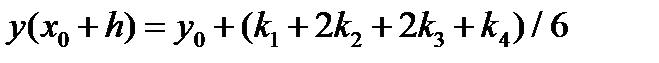 (5.20)
(5.20)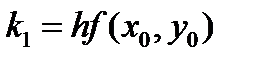
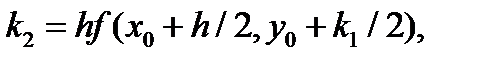


 (5.21)
(5.21)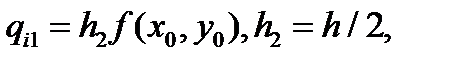
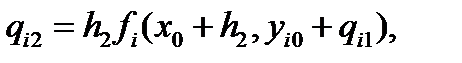


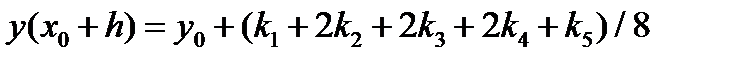 (5.22)
(5.22)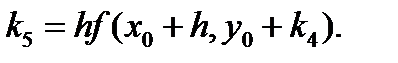
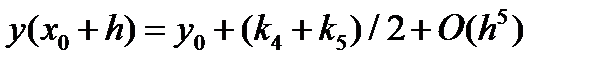 (5.23)
(5.23)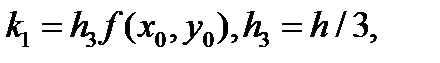
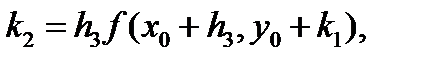

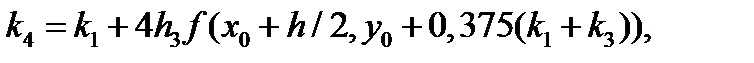
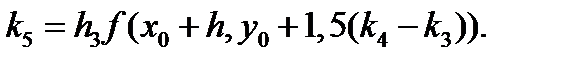
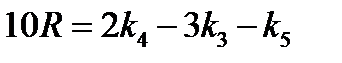 (5.24)
(5.24)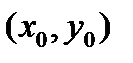 - Шаг h можно удвоить при выполнении условия:
- Шаг h можно удвоить при выполнении условия: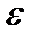 . (5.25)
. (5.25)


