
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерполяция каноническим полиномомСодержание книги
Поиск на нашем сайте
Одной из важнейших задач в процессе математического моделирования является вычисление значений функций, входящих в математическое описание модели. Для сложных моделей подобные вычисления могут быть трудоемкими даже при использовании ЭВМ. При выполнении программ, реализующих основные методы вычислительной математики, большая часть времени также затрачивается на вычисление функций. Используемые в математических моделях функции задаются как аналитическим способом, так и табличным, при котором функции известны только при дискретных значениях аргументов. Ограниченный объем памяти ПЭВМ не позволяет хранить подробные таблицы функций, желательно иметь возможность "сгущать"таблицы, заданные с крупным шагом аргумента. Поставленные проблемы решаются путем приближенной замены функции f(x) функцией Приближение функции f(x) более простой функцией В задачах электротехники широко используется аппроксимация функций для физических параметров сред, для задания характеристик активных и пассивных элементов электрических и магнитных цепей и т.д. В вычислительной математике аппроксимация функций является основой для разработки многих методов и алгоритмов [ 1 ]. Пусть функция f{x) задана таблицей значений, полученных из эксперимента или путем вычислений в последовательности значений аргумента
Таблица 2.1. Узлы и значения функции
Введем аппроксимирующую функцию
Свободные параметры Подобный способ введения аппроксимирующей функции называется лагранжевой интерполяцией, а соотношения (2.1)- условиями Ла-гранжа [2]. Задачей интерполяции в узком смысле считают нахождение приближенных значений табличной функции при аргументах х, не совпадающих с узловыми. Если значение аргумента х расположено между узлами В более общем плане с помощью интерполяции решают широкий круг задач численного анализа — дифференцирование и интегрирование функций, нахождение нулей и экстремумов функций, решение дифференциальных уравнений и т.д. Возможность решения подобных задач обусловлена достаточно простым видом аппроксимирующей функции Выберем в качестве аппроксимирующей функции
Свободными параметрами интерполяции с n являются коэффициенты полинома (2.2). Интерполяция полиномами обладает такими преимуществами, как простота вычислений их значений, дифференцирования и интегрирования.
Коэффициенты сn определим из условия Лагранжа
или
Система линейных алгебраических уравнений (2.3) относительно свободных параметров с, имеет решение, так как определитель системы отличен от нуля, если среди узлов х, нет совпадающих. Определитель системы (2.3) называется определителем Вандермонда и имеет аналитическое выражение [2]. Рассмотренный способ вычисления интерполяционного полинома не является эффективным по затратам времени и объему памяти ЭВМ. Независимо от формы записи полинома для заданной таблицы узлов и значений функции значение интерполяционного полинома является единственным. Это важное утверждение доказывается от противного [3]. Предположим, что для одной и той же табл. 2.1 с п + 1 узлом построены два полинома n-й степени Рп(х) и Qn(x) с разными коэффициентами. Запишем алгебраическое уравнение
левая часть которого будет также полиномом степени п. По основной теореме алгебры уравнение (2.4) имеет п корней. С другой стороны, в узлах
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 272; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.134.95 (0.006 с.) |

 , которую нетрудно вычислять при любом значении аргумента х в заданном интервале его изменения. Введенную функцию
, которую нетрудно вычислять при любом значении аргумента х в заданном интервале его изменения. Введенную функцию 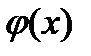 можно использовать не только для приближенного определения численных значений f(х), но и для проведения аналитических выкладок при теоретическом исследовании модели.
можно использовать не только для приближенного определения численных значений f(х), но и для проведения аналитических выкладок при теоретическом исследовании модели. называется аппроксимацией (от латинского approximo — приближаюсь). Близости этих функций добиваются путем введения в аппроксимирующую функцию
называется аппроксимацией (от латинского approximo — приближаюсь). Близости этих функций добиваются путем введения в аппроксимирующую функцию  свободных параметров
свободных параметров  и соответствующим их выбором.
и соответствующим их выбором. ,(табл. 2.1). Выбранные значения аргумента х называют узлами таблицы. Считаем, что узлы в общем случае не являются равноотстоящими.
,(табл. 2.1). Выбранные значения аргумента х называют узлами таблицы. Считаем, что узлы в общем случае не являются равноотстоящими.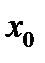 х0
х0


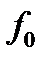


 так, чтобы она совпадала с табличными значениями заданной функции f(x) во всех узлах
так, чтобы она совпадала с табличными значениями заданной функции f(x) во всех узлах  :
: . (2.1)
. (2.1) определяются из системы (2.1).
определяются из системы (2.1).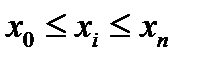 то нахождение приближенного значения функции f(x) называют интерполяцией, если интерполирующую функцию вычисляют вне интервала
то нахождение приближенного значения функции f(x) называют интерполяцией, если интерполирующую функцию вычисляют вне интервала  , то процесс называют экстраполяцией. Происхождение этих терминов связано с латинскими словами inter — между, внутри, pole — узел, extra — вне.
, то процесс называют экстраполяцией. Происхождение этих терминов связано с латинскими словами inter — между, внутри, pole — узел, extra — вне. .
. полином
полином  степени п в каноническом виде:
степени п в каноническом виде: .... (2.2)
.... (2.2)
 (2.3)
(2.3) (2.4)
(2.4) значения обоих полиномов совпадают со значениями аппроксимируемой функции
значения обоих полиномов совпадают со значениями аппроксимируемой функции  Значит узлы являются корнями уравнения (2.4), т.е. количество корней равно п + -1-1. Противоречие с основной теоремой алгебры приводит к тождеству Рп(х) = Qn(x), что и доказывает единственность интерполяционного полинома. Единственность позволяет вводить полиномы в формах, отличных от канонической (2.2).
Значит узлы являются корнями уравнения (2.4), т.е. количество корней равно п + -1-1. Противоречие с основной теоремой алгебры приводит к тождеству Рп(х) = Qn(x), что и доказывает единственность интерполяционного полинома. Единственность позволяет вводить полиномы в формах, отличных от канонической (2.2).


