
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы Адамса-Башфорта и Адамса-МаултонаСодержание книги
Поиск на нашем сайте
При решении задачи Коши методами Рунге-Кутта необходимо вычислять правые части ОДУ в нескольких точках на каждом шаге. Количество точек зависит от порядка используемого метода. После того, как искомая интегральная кривая у (х) определена в нескольких точках Алгоритмы многоточечных методов основываются на аппроксимации интерполяционными полиномами либо правых частей ОДУ, либо интегральных кривых Рассмотрим четырехточечный вариант одного из методов первого типа для задачи Коши, сформулированной в виде (5.5). С помощью любой из схем, рассмотренных в предыдущих разделах, вычислим решения f(x) = f(x,y(x)), значения которой в рассматриваемых точках обозначим В окрестности узлов
где Представим искомое решение в точке
где Дифференцируя полином (5.26), получим выражения для производных
Последнее соотношение при
Подставляя производные (5.28) в разложение (5.27), получим экс-траполяционную формулу Адамса-Башфорта [24]
имеющую пятый порядок локальной погрешности и четвертый — глобальной. Остаточный член формулы (5.29) равен Изменяя количество членов, учитываемых в ряде (5.27), можно получить схемы Адамса-Башфорта различных порядков. Формула Адамса для переменного шага приведена в [2]. В табл. 5.1 приведены формулы методов Адамса-Башфорта от первого до шестого порядка. Таблица 5.1. Методы Адамса-Башфорта
Анализ табл. 5.1 показывает, что метод Адамса-Башфорта порядка k требует k начальных значений: С целью уменьшения погрешности способом, аналогичным получению формулы (5.29), по узлам
Последняя формула является неявной, так как искомая величина Таким образом, вычисления на каждом шаге интегрирования дифференциального уравнения осуществляются по схеме Формулы (5.29) и (5.30) без изменения переносятся на системы ОДУ первого порядка, записанные в форме Коши. В табл. 5.2 приведены формулы методов Адамса-Маултона от первого до шестого порядка.
Методы Гира Одним из методов Рунге-Кутта получим решения у\, уч. Уз задачи Коши
Таблица 5.2. Методы Адамса-Маултона
в точках
где Левую часть уравнения (5.31) приближенно найдем путем дифференцирования по х полинома (5.32):
(5.33)
Разделенные разности для равноотстоящих узлов выражаются через узловые значения аппроксимируемой функции:
(5.34)
где Полагая в выражении для производной (5.33) значение аргумента
С другой стороны, уравнение (5.31) при
Приравняем правые части соотношений (5.35), (5.36) и найдем
Формула (5.37) представляет собой неявную схему Гира четвертого порядка для решения задачи Коши [24, 1]. Изменяя количество узлов Неявные алгоритмы Гира наиболее эффективны для решения так называемых жестких уравнений, особенностью которых является медленное изменение их решений при наличии быстро затухающих возмущений [25, 1]. Жесткими уравнениями моделируются процессы в нелинейных электрических цепях, и применение неявных методов уменьшает на несколько порядков время интегрирования по сравнению с явными методами [24,26].
Таблица 5.3. Методы Гира
Для нахождения значения
Приравнивая правые части исходного уравнения (5.31) при х = хз и выражения (5.38), получим схему прогноза, с помощью которой можно найти начальное приближение для решения уравнения (5.37):
Библиографический список 1. Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран, Паскаль. —Томск: МП "Раско", 1991. — 270с. 2. Калиткин Н.Н. Численные методы. — М.: Наука, 1978. —512 с. 3. Кунцман Ж. Численные методы: Пер. с фр. — М.: Наука, 1979. — 160 с. 4. Гилой В. Интерактивная машинная графика: Пер. с англ. — М.: Мир, 1981. —384 с. 5. Завьялов Ю.С., Квасов Б.И., Мирошниченко В.Л. Методы сплайн-функций. — М.: Наука, 1980. — 352 с. 6. Завьялов Ю.С., Леус В.А., Скороспелое В.А. Сплайны в инженерной геометрии. — М.: Машиностроение, 1985. — 224 с. 7. Де Бор К. Практическое руководство по сплайнам: Пер. с англ. — М.: Радио и связь, 1985. — 304 с. 8. Шуп Т. Решение инженерных задач на ЭВМ: Практическое pyKQ-водство: Пер. с англ. — М.: Мир, 1982. — 238 с. 9. Форсайт Дж, Моулер К- Машинные методы математических вычислений: Пер. с англ. — М.: Мир, 1980. — 280 с. 10. Справочник по специальным функциям с формулами, графиками и математическими таблицами: Пер. с англ. / Под. ред. М.Абрамовица и И.Стиган. — М.: Наука, 1979. — 832 с. 11. Бут Э Д. Численные методы: Пер. с англ. — М.: ГИФМЛ, 1959. — 240 с. 12. Никифоров А.Ф., Суслов СК-, Уваров В.Б. Классические ортогональные полиномы дискретной переменной. — М.: Наука, 1985. — 216с. 13. Гутер Р.С., Овчинский Б.В. Элементы численного анализа и математической обработки результатов опыта. 2-е изд., перераб. — М.: Наука, 1970. —432 с. 14. Львовский Е.Н. Статистические методы построения эмпирических формул — М.: Высш. шк., 1988. — 239 с. 15. Ивченко Г.И., Медведев Ю.И. Математическая статистика. —' М.: Высш. шк., 1984. — 248 с. 16. Мак-КракенД., Дорн У. Численные методы и программирование на Фортране. 2 -е изд. Пер. с англ./Под ред. Б.Н.Наймарка».— М.:Мир, 1977. —584 с. 17. Справочное пособие по приближенным методам решения задач высшей математики / Л.И.Бородич, А.И.Герасимович Н.П.Кеда, И.Н.Мелешко. — Минск: Вышэш. шк, 1986. — 189 с. 18. Крылов М.Т., Шульгина Л.Т. Справочная книга по численному интегрированию. — М.: Наука, 1966. — 370 с. 19. Ортега Дж., Пул У. Введение в численные методы решения дифференциальных уравнений: Пер. с англ. — М.: Наука, 1986. — 288 с. 20. Березин И.С., Жидков Н.П. Методы вычислений. Т. 2 2-е изд., пе-рераб. — М.: Наука, 1982. — 296 с. 21. Корн Г., Корн Т. Справочник по высшей математике для научных работников и инженеров. — М.: Наука, 1984. — 831 с. 22. Ланс Дж.Н. Численные методы для быстродейсвующих вычислительных машин: Пер. с англ. — М.: ИЛ, 1962. — 208 с. 23. Самарский А.А., Гулин А.В. Численные методы. — М.: Наука, 1989. — 432 с. 24. Чуд Л.О., Лин Пен-Мин. Машинный анализ электронных схем: Алгоритмы и вычислительные методы: Пер. с англ. — М.: Энергия, 1980. —640 с. 25. Деккер К., Вервер Я. Устойчивость методов Рунге-Кутты для жестких нелинейных дифференциальных уравнений: Пер. с англ. — М.: Мир, 1988. — 334 с. 26. Сигорский В.П., Петренко А.И. Алгоритмы анализа электронных схем — М.: Сов. радио, 1976. — 608 с.
Учебное издание Павел Григорьевич Колпахчьян, Ирина Борисовна Подберезная, Светлана Викторовна Чамлай
МЕТОДЫ ВЫЧИСЛЕНИЙ В ЗАДАЧАХ ЭЛЕКТРОАППАРАТОСТРОЕНИЯ, ЭЛЕКТРООБОРУДОВАНИЯ И ЭЛЕКТРИЧЕСКОГО ТРАНСПОРТА
Редактор Н.А.Юшко
Темплан 2012 г. ЛР 020417 от 12.02.12 г. Повписано в печать 19.12.2012 г. Формат 60 х 84 1/16. Бумага офсетная, Печать оперативная. Печ.л. 5,35. Уч. - изд. л. 5,5. Тираж 50.
Южно-Российский государственный технический университет Редакционно-издательский отдел ЮРГТУ Адрес университета: 346428, г.Новочеркасск, ул. Просвещения 132 Центр оперативной полиграфии ЮРГТУ(НПИ) тел. 55-222. Заказ №
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 3003; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.91.116 (0.009 с.) |

 можно применить алгоритмы интерполяции и сократить количество правых частей ОДУ для получения решения в очередной точке xn+i. Подобные методы называют многоточечными или многошаговыми. Известно несколько типов таких методов [23, 24, 1].
можно применить алгоритмы интерполяции и сократить количество правых частей ОДУ для получения решения в очередной точке xn+i. Подобные методы называют многоточечными или многошаговыми. Известно несколько типов таких методов [23, 24, 1]. .
. заданного дифференциального уравнения в точках
заданного дифференциального уравнения в точках  . Правая часть уравнения f(x, у) на интегральной кривой, соответствующей начальному условию, будет функцией только одного аргумента х
. Правая часть уравнения f(x, у) на интегральной кривой, соответствующей начальному условию, будет функцией только одного аргумента х .
.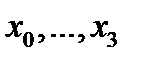 функцию f(x) приближенно заменим интерполяционным полиномом Ньютона (2.6):
функцию f(x) приближенно заменим интерполяционным полиномом Ньютона (2.6):
 , (5.26)
, (5.26) — разделенные разности (2.10) — (2.12).
— разделенные разности (2.10) — (2.12).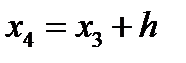 в виде тейлоровского разложения около точки
в виде тейлоровского разложения около точки  :
: (5.27)
(5.27) — производные по х от правой части дифференциального уравнения в точке
— производные по х от правой части дифференциального уравнения в точке  .
.



 в случае равноотстоящих узлов после подстановки в них разделенных разностей (2.10) — (2.12) принимает вид
в случае равноотстоящих узлов после подстановки в них разделенных разностей (2.10) — (2.12) принимает вид
 (5.28)
(5.28)

 (5.29)
(5.29) [2]. Значительная величина коэффициента в остаточном члене обусловлена тем, что точка
[2]. Значительная величина коэффициента в остаточном члене обусловлена тем, что точка  лежит вне интервала расположения узлов
лежит вне интервала расположения узлов 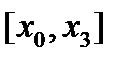 , по значениям функции f(x), в которых построен интерполяционный полином. Таким образом, мы имеем дело с экстраполяцией, погрешность которой в соответствии с оценкой (2.15) всегда больше, чем при интерполяции.
, по значениям функции f(x), в которых построен интерполяционный полином. Таким образом, мы имеем дело с экстраполяцией, погрешность которой в соответствии с оценкой (2.15) всегда больше, чем при интерполяции.





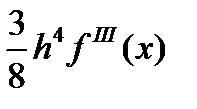




 +
+
 }
}



 Поэтому его называют k - шаговым.
Поэтому его называют k - шаговым. строится интерполяци онная формула Адамса - Маултона
строится интерполяци онная формула Адамса - Маултона (5.30)
(5.30) необходима для вычисления значений функции
необходима для вычисления значений функции  , входящей в правую часть. Выражение(5.30) можно рассматривать как нелинейное уравнение относительно неизвестной величины
, входящей в правую часть. Выражение(5.30) можно рассматривать как нелинейное уравнение относительно неизвестной величины  и решать его одним из методов, описанных выше. Наиболее часто здесь используется метод простых итераций, хотя в некоторых случаях оказывается более предпочтительным метод Ньютона [24]. Следует иметь в виду, что каждая итерация потребует нового вычисления правой части дифференциального уравнения f(x, у). Решение, определенное по экстра-поляционной формуле (5.29), обычно выбирается в качестве начального приближения для итерационных методов, поэтому выражение (5.29) рассматривается как формула прогноза, тогда выражение (5.30) является формулой коррекции.
и решать его одним из методов, описанных выше. Наиболее часто здесь используется метод простых итераций, хотя в некоторых случаях оказывается более предпочтительным метод Ньютона [24]. Следует иметь в виду, что каждая итерация потребует нового вычисления правой части дифференциального уравнения f(x, у). Решение, определенное по экстра-поляционной формуле (5.29), обычно выбирается в качестве начального приближения для итерационных методов, поэтому выражение (5.29) рассматривается как формула прогноза, тогда выражение (5.30) является формулой коррекции. , где этапы вычислительного процесса обозначены буквами Р — прогноз, Е — вычисление функции f(x, у), С — коррекция, т — количество итераций коррекции [9]. В [2] приводится эмпирическое правило, согласно которому погрешность решения убывает только до тех пор, пока
, где этапы вычислительного процесса обозначены буквами Р — прогноз, Е — вычисление функции f(x, у), С — коррекция, т — количество итераций коррекции [9]. В [2] приводится эмпирическое правило, согласно которому погрешность решения убывает только до тех пор, пока  , где p — порядок используемого неявного метода. Следовательно, для метода четвертого порядка не следует выполнять более четырех итераций коррекции. С другой стороны, в [9] отмечается, что схема
, где p — порядок используемого неявного метода. Следовательно, для метода четвертого порядка не следует выполнять более четырех итераций коррекции. С другой стороны, в [9] отмечается, что схема  является более устойчивой в смысле накопления вычислительной погрешности по сравнению со схемой
является более устойчивой в смысле накопления вычислительной погрешности по сравнению со схемой 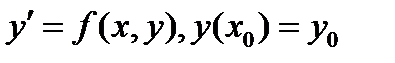 (5.31)
(5.31)
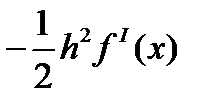














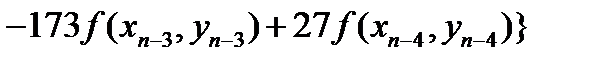

 В окрестностях узлов
В окрестностях узлов 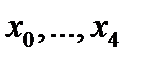 искомое решение у(х) приближенно замениминтерполяционным полиномом Ньютона четвертой степени, аналогичным (5.26):
искомое решение у(х) приближенно замениминтерполяционным полиномом Ньютона четвертой степени, аналогичным (5.26):
 (5.32)
(5.32)

 — разделенные разности первого — четвертого порядков.
— разделенные разности первого — четвертого порядков.





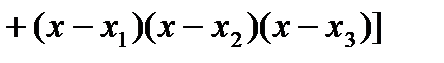




 .
.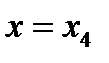 и учитывая значения разделенных разностей (5.34), получим
и учитывая значения разделенных разностей (5.34), получим (5.35)
(5.35) принимает вид
принимает вид (5.36)
(5.36) . (5.37)
. (5.37) можно аналогичным способом получить формулы Гира как более низких, так и более высоких порядков. В табл. 5.3 приведены формулы методов Гира от первого до шестого порядка.
можно аналогичным способом получить формулы Гира как более низких, так и более высоких порядков. В табл. 5.3 приведены формулы методов Гира от первого до шестого порядка.





 +
+


 +
+ 

 +
+


 из уравнения (5.37) можно применить метод простых итераций, однако для реализации достоинств неявного метода в отношении выбора шага при интегрировании жестких уравнений в [24] рекомендуется использовать метод Ньютона. Для любого из выбранных методов требуется знать начальное приближение к искомой величине у4- Полагая в выражении для производной (5.33) значение аргумента х = хз, будем иметь
из уравнения (5.37) можно применить метод простых итераций, однако для реализации достоинств неявного метода в отношении выбора шага при интегрировании жестких уравнений в [24] рекомендуется использовать метод Ньютона. Для любого из выбранных методов требуется знать начальное приближение к искомой величине у4- Полагая в выражении для производной (5.33) значение аргумента х = хз, будем иметь (5.38)
(5.38) .
.


