
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сглаживание экспериментальных данных с ошибкамиСодержание книги
Поиск на нашем сайте
Если некоторый набор экспериментальных данных содержит случайные отклонения, а зависимость Линейное сглаживание для п точек по трем ординатам проводится с помощью формул:
Линейное сглаживание по пяти ординатам проводится по формулам:
φ 0 = (Зƒ0 + 2ƒ1 + ƒ2 - ƒ4)/4, i = 0, φ 1 = (4ƒ0 + 3ƒ1 + 2ƒ2 + ƒ3)/10, i = 1, φ i = (ƒi-2 + ƒi-1 + ƒi + ƒi+1)/5, 2 ≤ i ≤ n-2, (3.27) φ n-1 = (ƒn-3 + 2ƒn-2 + 3ƒn-1 + 4ƒn)/10, i = n-l. φ n = (3ƒn + 2ƒn-1 + ƒn-2 - ƒn-4)/5, i = n.
Для функций ƒi (xi),сильно отличающихся от линейных используется нелинейное сглаживание с помощью полиномов высоких степеней m. При m = 3 необходимое число координат составляет семь. Сглаживание при семи ординатах производится по формуле
φ i = (a1ƒi-3 + a2 ƒi-2 + a3 ƒi-1 + a4 ƒi + a5 ƒi+1 + a6 ƒi+1 + a7 ƒi+3)/42, (3.28)
где коэффициенты a1 - a7 берутся из табл. 3.2 в зависимости от номера ординаты. Таблица 3.2. Коэффициенты формулы (3.28)
Глава 4 Определенные интегралы Классификация методов Ставится задача вычислить интеграл вида b a где a и b — нижний и верхний пределы интегрирования; ƒ(x) — непрерывная функция на отрезке [ а, b ]. К численному интегрированию обращаются, когда нельзя через элементарные функции аналитически записать первообразную интеграла (4.1) или когда подобная запись имеет сложный вид. Сущность большинства методов вычисления определенных интегралов состоит в замене подынтегральной функции ƒ(x) аппроксимирующей функцией φ(x), для которой можно легко записать первообразную в элементарных функциях, т.е. ь ь ∫ƒ(x)dx = ∫ φ(x)dx + R = S + R, (4.2) а а где S — приближенное значение интеграла; R — погрешность вычисления интеграла. Используемые на практике методы численного интегрирования можно сгруппировать в зависимости от способа аппроксимации подынтегральной функции. Дадим краткую характеристику групп наиболее распространенных методов.
Методы Ньютона-Котеса основаны на полиномиальной аппроксимации подынтегральной функции. Методы этого класса отличаются друг от друга степенью используемого полинома, от которой зависит количество узлов, где необходимо вычислить функцию ƒ(x). Алгоритмы методов просты и легко поддаются программной реализации. Сплайновые методы базируются на аппроксимации подынтегральной функции сплайнами, представляющими собой кусочный полином. Методы различаются по типу выбранных сплайнов. Такие методы имеет смысл использовать в задачах, где алгоритмы сплайновой аппроксимации применяются для обработки данных. В методах наивысшей алгебраической точности (методы Гаусса-Кристоффеля и др.) используют неравноотстоящие узлы, расположенные по алгоритму, обеспечивающему минимальную погрешность интегрирования для наиболее сложных функций при заданном количестве узлов. Методы различаются способами выбора узлов и широко используются для интегрирования, в том числе они применимы и для несобственных интегралов. Хотя из-за необходимости хранения числовых констант и стандартизации пределов интегрирования программы указанных методов требуют несколько большего объема памяти по сравнению с методами Ньютона-Котеса. В методах Монте-Карло узлы выбираются с помощью датчика случайных чисел, ответ носит вероятностный характер. Методы оказываются эффективными при вычислении интегралов большой кратности. В класс специальных группируются методы, алгоритмы которых разрабатываются на основе учета особенностей конкретных подынтегральных функций, что позволяет существенно сократить время и уменьшить погрешность вычисления интегралов. Независимо от выбранного метода в процессе численного интегрирования необходимо вычислить приближенное значение S интеграла (4.1) и оценить погрешность R (4.2). Погрешность будет уменьшаться при увеличении количества разбиений N интервала интегрирования [а, b]за счет более точной аппроксимации подынтегральной функции, однако при этом будет возрастать погрешность за счет суммирования частичных интегралов, и последняя погрешность с некоторого значения No становится преобладающей (рис. 4.1) [ 16, 1 ].
Рис. 4.1. Зависимость полной погрешности R от количества разбиений N интервала интегрирования
Это обстоятельство должно предостеречь от выбора чрезмерно большого числа N и привести к необходимости разработки способа оценки погрешности R выбранного метода интегрирования.
Методы прямоугольников Рассмотрим сначала простейшие методы из класса методов Ньютона-Котеса, когда подынтегральную функцию f( x ) на интервале интегрирования заменяем полиномом нулевой степени, т.е. константой. Подобная замена является неоднозначной, так как константу можно выбрать равной значению подынтегральной функции в любой точке интервала интегрирования. Приближенное значение интеграла определится как площадь прямоугольника, одна из сторон которого есть длина отрезка интегрирования, а другая — аппроксимирующая константа. Отсюда происходит и название методов. Как будет показано ниже, из методов прямоугольников наименьшую погрешность имеет метод средних прямоугольников, когда константу берем равной значению f (x)в средней точке х интервала интегрирования [ x i-1, xi ](рис. 4.2).
F(x)
х 0 х х 1 хп х Рис. 4.2. Метод средних прямоугольников
Методы левых (рис. 4.3а) и правых прямоугольников (рис. 4.36), заменяющих интеграл нижней и верхней суммами Дарбу, имеют сравнительно высокую погрешность. Запишем выражение для интеграла в интервале [ xi, xi + h ], полученное методом средних прямоугольников
xi + h ∫ ƒ(x)dx =hƒ( xi
х0 х1 хп х a) х0 х1 хп х б) Рис. 4.3. Методы левых (а) и правых (б) прямоугольников
где
в малой окрестности точки x этот ряд с высокой точностью представляет функцию f (x)при небольшом количестве членов разложения. Поэтому, подставляя под интеграл вместо функции f (x)ее тейлоровское разложение (4.4) и интегрируя его почленно, можно вычислить интеграл с любой наперед заданной точностью:
h³ =hƒ( 24 При интегрировании и подстановке пределов получаем, что все интегралы от членов ряда (4.4), содержащих нечетные степени (x — Сравнивая отношения (4.3) и (4.5), можно записать выражение для погрешности R.. При малой величине шага интегрирования h основной вклад в погрешность R будет вносить первое слагаемое, которое называется главным членом погрешности R0iвычисления интеграла на интервале [xi, xi + h]: h³ R0i=—ƒ″(xi). (4.6) 24 Главный член полной погрешности для интеграла на всем интервале [ x 0 , x n ] определится путем суммирования погрешностей на каждом частичном интервале [ x i, x i + h ]:
К последнему интегралу мы перешли, используя метод средних прямоугольников для функции f"(x). Формула (4.7) представляет собой теоретическую оценку погрешности вычисления интеграла методом средних прямоугольников, эта оценка является априорной, так как не требует знания значения вычисляемого интеграла. Оценка (4.7) не удобна для практического вычисления погрешности, но полезна для установления структуры главного члена погрешности. Степень шага h, которой пропорциональна величина R0, называется порядком метода интегрирования. Метод средних прямоугольников имеет второй порядок.
Аналогично проведем априорную оценку метода левых прямоугольников. Разложим подынтегральную функцию в ряд Тейлора около точки x = xi
Интегрируя разложение (4.8) почленно на интервале
где первое слагаемое есть приближенное значение интеграла, вычисленное по методу левых прямоугольников, второе слагаемое является главным членом погрешности
На интервале
Таким образом, метод левых прямоугольников имеет первый порядок, кроме того, погрешность будет больше по сравнению с методом средних за счет интеграла от производной f'(x) и коэффициента в знаменателе (4. 10). Обычно для большинства функций выполняется неравенство
Однако, если подынтегральная функция f(x) определяется из эксперимента в дискретном наборе узлов, то метод средних прямоугольников применить нельзя из-за отсутствия значений f(x) в средних точках
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.5.88 (0.007 с.) |

 (
( ) задана значениями ft для равноотстоящих абсцисс
) задана значениями ft для равноотстоящих абсцисс 

 (3.26)
(3.26)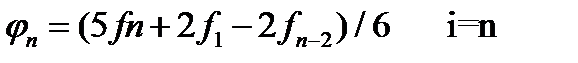


 )+ R, (4.3)
)+ R, (4.3)
 = xi + h/2, R = Jточн- Jприбл, и оценим погрешность R. Для этого разложим подынтегральную функцию ƒ(x) в ряд Тейлора около средней точки x
= xi + h/2, R = Jточн- Jприбл, и оценим погрешность R. Для этого разложим подынтегральную функцию ƒ(x) в ряд Тейлора около средней точки x (4.4)
(4.4)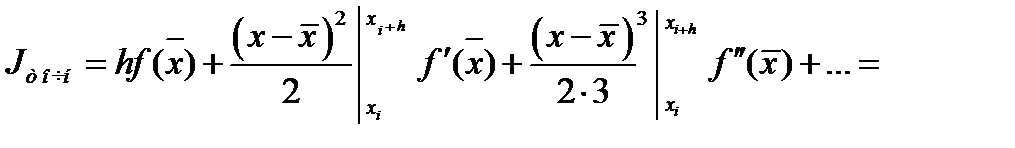
 ) +—ƒ″(
) +—ƒ″( ) + … (4.5)
) + … (4.5)  ) обращаются в нуль.
) обращаются в нуль. (4.7)
(4.7) . (4.8)
. (4.8) получим
получим

 (4.9)
(4.9)
 главный член погрешности интегрирования получим суммированием частичных погрешностей (4.9):
главный член погрешности интегрирования получим суммированием частичных погрешностей (4.9):
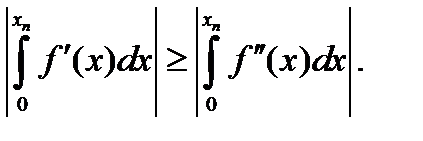
 . В этом случае для интегрирования используются другие методы Ньютона-Котеса.
. В этом случае для интегрирования используются другие методы Ньютона-Котеса.


