
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Базис в виде ортогональных полиномов дискретной переменной
Построим систему базисных функций φk (x)так, чтобы обращались в нуль скалярные произведения на дискретном множестве узловых точек (3.5), тогда матрица Грамма (3.4) будет диагональной, что позволит отказаться от использования процедур численного решения системы нормальных уравнений. В зависимости от распределения погрешности обрабатываемых данных можно построить полиномы дискретной переменной, ортогональные с соответствующими дискретными весовыми функциями p(x j). Из классических ортогональных полиномов дискретной переменной известны полиномы Хана, Мейкснера, Кравчука и Шарлье[12]. Рассмотрим алгоритм [13,1] построения полиномов Чебышева tk(x)дискретной переменной, которые являются важным частным случаем полиномов Хана с единичной весовой функцией. Полином нулевой степени выберем единичным t 0 (x) = 1, (3.14) а полином первой степени возьмем в виде t 1 (x) == х - a 1, (3.15) где коэффициент a 1 определим из условий ортогональности (t 0 , t 1) = 0. (3.16) Запишем условие (3.16) в развернутом виде п п п ∑ l(xi – а1) = ∑ х k - a ∑ l = 0, i =0 i=0 t=0 откуда получим п а1 = ∑ xi /(n + l). (3.17) i =0 Полином второй степени также представим в общем виде с неопределенными коэффициентами а21и а20: t2(x) = х2 + а21х + а20, которые найдем из двух условий ортогональности: (t 0 , t 2) = 0, (t 1, t 2) = 0. Аналогичным способом запишем ортогональный полином степени k:
t k{x) = хk + аk,k-1хk-1 +…+ аk0. Для полиномов Чебышева дискретной переменной установлена двух- слойная рекуррентная формула [13], по которой можно вычислить полином любой степени через начальные полиномы (3.14) и (3.15)
t k+1(x) = (x- a k+1) t k(x) – b k+1 t k-1(x), (3.18)
n n a k+1 = ∑ x i tk 2 (x i) ⁄ ∑ t k (x i) i =0 i =0 n n b k+1 = ∑ tk 2 (x i) ⁄ ∑ tk-1 2 (x i) (3.19) i=0 i=0 Аппроксимирующая функция φ(x)определяется, как и ранее (3.3), в виде линейной комбинации базисных функций, в качестве которых теперь выбраны полиномы Чебышева дискретной переменной t k(x): m φ(x) = ∑ ck tk (x) (3.20) k=0 Вследствие диагональноcти матрицы Грамма коэффициенты с k линейной комбинации (3.20) определяются как частные от деления правых частей (3.6) системы нормальных уравнений на диагональные элементы этой матрицы: n n c k = ∑ ƒ(x i) tk (x i) ⁄ ∑ tk 2 (x i) (3.21) i=0 i=0 При увеличении количества базисных функций.в сумме (3.20) не придется пересчитывать коэффициенты с k, определенные с меньшим значением m.
3.5. Линейный вариант метода наименьших квадратов На практике довольно часто оказывается возможным при обработке экспериментальных данных ограничиться построением линейной аппроксимирующей функции φ(x) = а + bх. (3.22) Для многих нелинейных зависимостей с двумя параметрами аи b можно свести нелинейную зависимость к линейной, φ' (х) = а'(х) + b', с помощью преобразования х→x' и ƒ→ƒ '[2, 14, 1]. После проведения линейной регрессии получим значения a ' и b ', которые после преобразований a' → а и b' → b дают искомые параметры а и bнелинейной зависимости. Преобразования, сводящие нелинейную зависимость к линейной даны в табл.3.1.
Таблица 3.1. Преобразования х, у в х', у' и а', b' в a, b
Для коэффициентов а и b (см. формулу (3.22)) из общего алгоритма МНК получим выражения
где
Погрешность вычисления коэффициентов (3.23) определяется по формулам
где Среднеквадратичное отклонение аппроксимирующей функции ip(x) от исходной определяется по формуле (3.1).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.233.72 (0.01 с.) |
 (3.23)
(3.23)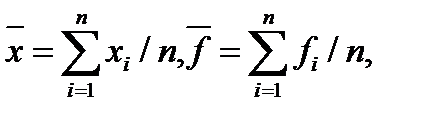 (3.24)
(3.24)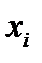 ,
, 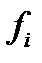 — узлы и значения аппроксимируемой функции в них; n — количество узлов.
— узлы и значения аппроксимируемой функции в них; n — количество узлов.
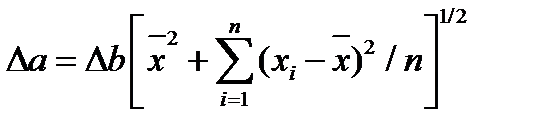 (3.25)
(3.25)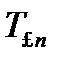 — коэффициент Стьюдента для п измерений и доверительной вероятности £ [15].
— коэффициент Стьюдента для п измерений и доверительной вероятности £ [15].


