
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Апостериорные оценки погрешностей по Рунге и Эйткену
Априорные оценки погрешностей (4.7) и (4.10) можно записать в виде
где А — коэффициент, зависящий от метода интегрирования и вида подынтегральной функции; h — шаг интегрирования; р — порядок метода. Зависимости (4.11) подчиняется главный член погрешности большинства методов численного интегрирования. При численном дифференцировании погрешность также может быть оценена с помощью формулы (4.11), при этом порядок р зависит от количества узловых точек. Пусть вычисляется значение некоторой переменной w с шагом /г, тогда
где
где коэффициент пропорциональности к может быть как больше, так и меньше единицы. Коэффициент А в выражениях (4.12) и (4.13) будет одинаковым, так как вычисляется одна и та же переменная, одним и тем же методом, а от величины шага h значение А не зависит. Пренебрегая бесконечно малыми величинами, приравняем правые части соотношений (4.12) и (4.13) с учетом формулы (4.11) и получим
откуда найдем главный член погрешности
Формула (4.14) называется формулой Рунге [2, 1] и позволяет путем двойного просчета величины w с шагами h и kh оценить погрешность. Так как оценка осуществляется после вычисления, то она является апостериорной. Формула (4.14) имеет большое практическое значение, так как позволяет провести оценку погрешности без изменения алгоритма используемого вычислительного процесса. При уменьшении шага h главный член погрешности Rо будет стремиться к полной погрешности R. После определения Rо можно вычислить уточненное значение искомой величины
последнее выражение называют второй формулой Рунге. К сожалению, погрешность уточненного значения остается неопределенной, хотя, как правило, она меньше значения Формулы Рунге справедливы для всех вычислительных процессов, для которых выполняется степенной закон (4.11). Для определения порядка метода р необходимо проведение априорной оценки погрешности, что не всегда легко осуществить. Английский математик Эйткен предложил способ оценки погрешности для случая, когда порядок р метода неизвестен. Более того, алгоритм Эйткена позволяет опытным путем определить и порядок метода. Для этого необходимо третий раз вычислить значение величины w с шагом k2h, т.е.
или
Приравнивая правые части выражений (4.13) и (4.16), получим соотношение
Подставив в это соотношение значение Rо из первой формулы Рунге (4.14), найдем
Полученное соотношение (4.17) вместе с первой формулой Рунге (4.14) позволяет оценить погрешность при использовании вычислительного метода с неизвестным порядком р. Более того, порядок р можно определить, логарифмируя левую и правую части формулы (4.17): Для выбранного вычислительного процесса алгоритм Эйткена достаточно применить только один раз при определении порядка метода, а затем использовать формулу Рунге, требующую только двукратного вычисления искомой величины. Формулу (4.14) можно использовать для тестирования программ, реализующих вычислительные методы с известной априорной погрешностью. Априорный и апостериорный порядки должны получаться совпадающими для правильных программ. Конечно, это совпадение будет приближенным, так как при получении алгоритмов Рунге и Эйткена учитывались только главные члены погрешности.
Метод трапеций Подинтегральную функцию заменим на участке
Априорную погрешность R метода трапеций получим путем интегрирования тейлоровского разложения подынтегральной функции около ТОЧКИ Xi
С помощью разложения (4.20) вычислим подынтегральную функцию в точке
откуда
Подставляя произведение (4.22) в выражение (4.21), получим
Следовательно, главный член погрешности метода трапеций на одном интервале будет
Если интегрирование проводится путем разбиения отрезка [ x0;xп ] на несколько интервалов, то общую погрешность получим суммированием частичных погрешностей (4.24):
Получили, на первый взгляд, несколько неожиданный результат, оказалось, что метод трапеций имеет погрешность в два раза больше по абсолютной величине, чем метод средних прямоугольников, хотя аппроксимация подынтегральной функции проводилась полиномом первой, а не нулевой степени. По-видимому, выбранный вариант аппроксимации подынтегральной функции прямой, проходящей через ее значения на границах, не является оптимальным. Задача выбора способа аппроксимации полиномом заданной степени с наименьшей возможной погрешностью была решена Гауссом, что привело к развитию целого класса методов. Как видно из выражения (4.25), метод трапеций, как и метод средних прямоугольников, имеет второй порядок. Если подынтегральная функция задана аналитически, то предпочтительнее из методов второго порядка применять метод средних прямоугольников вследствие его меньшей погрешности.
Метод Симпсона Подынтегральную функцию f(x) заменим интерполяционным полиномом второй степени Р2(х) — параболой, проходящей через узлы
где R — погрешность вычисления интеграла.
x0 xi x2 x Рис. 4.5. Метод Симпсона Для записи полинома Р2{х) воспользуемся интерполяционной формулой Ньютона (2.6) для трех узлов:
где
h - расстояние между узлами. Введем новую переменную
Теперь вычислим интеграл от полинома (4.27):
Последнее соотношение называют квадратурной формулой Симпсона или формулой парабол. Формулу Симпсона можно получить и с помощью первой и второй формул Рунге, примененных к вычислению интеграла методом трапеций. Запишем два приближенных значения интеграла от функции f(x) на интервале [
Интегралы (4.29) подставим в формулы (4.14) и (4.15) и получим уточненное значение интеграла
которое совпадает с формулой Симпсона (4.28). Для оценки погрешности формулы Симпсона разложим подынтегральную функцию f(x) в ряд Тейлора около точки х\ и проинтегрируем разложение почленно на интервале [
(4.30)
Суммируя разложения около точки хг для функции f(x) в узлах x0 и x2, получим, что
тогда интеграл (4.30) принимает вид
Первое слагаемое в правой части формулы (4.31) совпадает с формулой Симпсона, значит, второе слагаемое является главным членом погрешности для интеграла на интервале [
Если интеграл вычисляется на интервале [
тогда полная погрешность запишется в виде
следовательно, формула Симпсона имеет четвертый порядок точности с очень малым численным коэффициентом в остаточном члене. Формула Симпсона позволяет получить высокую точность, если четвертая производная подынтегральной функции не слишком велика. В противном случае методы второго порядка могут дать большую точность, чем метод` Симпсона. Например,`[17],для`функции
Методы Ньютона-Котеса В формулах Ньютона-Котеса порядок полинома п, которым заменяется подынтегральная функция f(x) может принимать различные значения. В этом случае на интервале [а, Ь] интеграл равен
где В табл. 4.1 приведены значения
Таблица 4.1. Коэффициенты формулы Ньютона-Котеса
|
|||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 545; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.221.204 (0.028 с.) |
 , (4.11)
, (4.11) , (4.12)
, (4.12) — приближенное значение w;
— приближенное значение w;  — главный член погрешности; О (hp+1) — бесконечно малая величина порядка hp+1. Вычислим ту же самую переменную w с шагом kh
— главный член погрешности; О (hp+1) — бесконечно малая величина порядка hp+1. Вычислим ту же самую переменную w с шагом kh , (4.13)
, (4.13)
 (4.14)
(4.14) (4.15)
(4.15) .
.
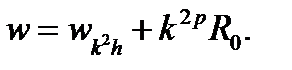 (4.16)
(4.16)
 (4.17)
(4.17) (4.18)
(4.18) полиномом первой степени
полиномом первой степени  . Как и в методах прямоугольников, такая аппроксимация неоднозначна. Одним из возможных способов является проведение прямой через значения функции на границах интервала интегрирования (рис. 4.4). В этом случае приближенное значение ин-ч теграла определяется как площадь трапеции:
. Как и в методах прямоугольников, такая аппроксимация неоднозначна. Одним из возможных способов является проведение прямой через значения функции на границах интервала интегрирования (рис. 4.4). В этом случае приближенное значение ин-ч теграла определяется как площадь трапеции: (4.19)
(4.19) (4.20)
(4.20) (4.21)
(4.21)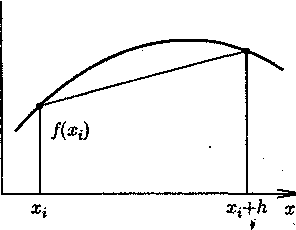
 :
: ,
, (4.22)
(4.22) (4.23)
(4.23) (4.24)
(4.24) (4.25)
(4.25) (рис. 4.5), тогда
(рис. 4.5), тогда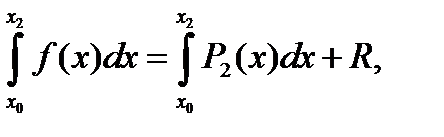

 , (4.26)
, (4.26)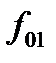 и
и  — разделенные разности, определяемые по формулам -
— разделенные разности, определяемые по формулам -

 , тогда
, тогда  и полином (4.26) принимает вид
и полином (4.26) принимает вид . (4.27)
. (4.27) (4.28)
(4.28) ,
,  ] с шагами h и 2h по формуле трапеций (4.19).:
] с шагами h и 2h по формуле трапеций (4.19).: (4.29)
(4.29)



 (4.31)
(4.31) , х2]
, х2] (4.32)
(4.32) ,
,  ] путем разбиения его на четное число подьштегралов [
] путем разбиения его на четное число подьштегралов [  ], на каждой паре которых применяется формула Симпсона для узлов
], на каждой паре которых применяется формула Симпсона для узлов 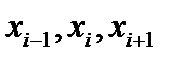 , то полная погрешность будет суммой правых частей соотношения (4.32). При малой величине шага h на основании метода средних прямоугольников получим
, то полная погрешность будет суммой правых частей соотношения (4.32). При малой величине шага h на основании метода средних прямоугольников получим ,
, (4.33)
(4.33) формула трапеций при n = 2 для интеграла в пределах [—1,1] дает точный результат, равный 4, тогда как по формуле Симпсона получим результат, не совпадающий даже по знаку (—8/3).
формула трапеций при n = 2 для интеграла в пределах [—1,1] дает точный результат, равный 4, тогда как по формуле Симпсона получим результат, не совпадающий даже по знаку (—8/3).
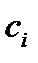 — коэффициенты Ньютона-Котеса;
— коэффициенты Ньютона-Котеса;  — общий знаменатель дробей, выражающих коэффициенты в формуле численного интегрирования;
— общий знаменатель дробей, выражающих коэффициенты в формуле численного интегрирования;  — относительные координаты (на промежутке [0,1])узловых точек, по которым строится интерполирующий полином.
— относительные координаты (на промежутке [0,1])узловых точек, по которым строится интерполирующий полином.
 и
и  , входящих в формулу (4.34), для п = 1... 5 и выражения для главного члена погрешности
, входящих в формулу (4.34), для п = 1... 5 и выражения для главного члена погрешности  . При п = 1 формулы Ньютона-Котеса дают формулу трапеций, п = 2 — формулу Симпсона.
. При п = 1 формулы Ньютона-Котеса дают формулу трапеций, п = 2 — формулу Симпсона.


