
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
П.Г. Колпахчьян, И. Б. Подберезная, С.В.Чамлай, Д.В. БатищевСтр 1 из 14Следующая ⇒
П.Г. Колпахчьян, И. Б. Подберезная, С.В.Чамлай, Д.В. Батищев
Методы вычислений в задачах электроаппаратостроения, электрооборудования и электрического транспорта: Методические указания к проведению вычислительной практики. Юж.-Рос. гос. техн. ун-т(НПИ). Новочеркасск: ЮРГТУ(НПИ), 2012. - 75с.
Настоящие указания содержат краткое описание основных методов решения систем обыкновенных дифференциальных уравнений, систем линейных и нелинейных уравнений, аппроксимации функции по методу наименьших квадратов, которые широко используются при моделировании и расчётах электрических аппаратов, электрооборудования и электрического транспорта. Приводятся некоторые стандартные подпрограммы, обращения к ним и варианты заданий. Указания предназначены для студентов первого и второго курсов дневной и заочной форм обучения направления 14040062 «Электроэнергетика и электротехника» ФГС ВПО (III поколения) профилей №9 Электрические и электронные аппараты, №12 Электрический транспорт, №16 Электрооборудование и электрохозяйство предприятий, организаций и учреждений. Методические указания утверждены на заседании кафедры «Электрические и электронные аппараты», «Электрический транспорт» протокол №7, от «29»февраля 2012г.
Ó Южно-Российский государственный технический университет, 2012 Ó Колпахчьян П.Г., Подберезная И. Б., Чамлай С.В., Батищев Д.В., 2012 Оглавление Предисловие. 5 Глава 1. Решение алгебраических уравнений и их систем.. 7 1.1. Решение систем линейных алгебраических уравнений. 7 1.1.1. Итерационные методы решения систем линейных алгебраических уравнений 7 1.1.2. Факторизация и типовые схемы решений. 9 1.1.3. Метод Гаусса и LU — разложение. 11 1.1.4. Метод Гаусса-Жордана обращения матриц. 13 1.1.5. Метод квадратного корня (Холесского) 13 1.1.6. Метод вращений. 15 1.1.7. Итерационное уточнение. 16 1.1.8. Решение преопределенных систем линейных алгебраических уравнений 17 1.2 Решение систем нелинейных алгебраических уравнений. 18 1.2.1.Метод последовательных приближений. 19 1.2.2. Метод Ньютона. 20 1.2.3. Метод Ньютона по параметру. 21 Глава 2. Интерполяция зависимостей. 23 2.1. Интерполяция каноническим полиномом. 23 2.2. Интерполяция полиномом Лагранжа. 25 2.3. Интерполяция полиномом Ньютона. 26
2.4. Применение интерполяции для решения уравнений. 28 2.5. Интерполяция сплайнами. 30 Глава 3. Метод наименьших квадратов. 34 3.1. Общие положения. 34 3.2. Степенной базис. 36 3.3. Базис в виде классических ортогональных полиномов. 36 3.4. Базис в виде ортогональных полиномов дискретной переменной. 38 3.5. Линейный вариант метода наименьших квадратов. 39 3.6. Сглаживание экспериментальных данных с ошибками. 40 Глава 4. Определенные интегралы.. 42 4.1. Классификация методов. 42 4.2. Методы прямоугольников. 43 4.3. Апостериорные оценки погрешностей по Рунге и Эйткену. 46 4.4. Метод трапеций. 48 4.5. Метод Симпсона. 49 4.6. Методы Ньютона-Котеса. 51 4.7. Вычисление интегралов с заданной точностью.. 52 4.8. Применение сплайнов для численного интегрирования. 54 4.9. Методы наивысшей алгебраической точности. 54 4.10 Несобственные интегралы.. 58 4.11 Вычисление кратных интегралов. 59 Глава 5. Решение обыкновенных дифференциальных уравнений. 60 5.1. Типы задач для обыкновенных дифференциальных уравнений. 60 5.2. Метод Эйлера. 61 5.3. Методы Рунге-Кутта. 63 5.4. Метод Рунгe-Кутта-Мерсона. 66 5.5. Методы Адамса-Башфорта и Адамса-Маултона. 67 5.6. Методы Гира. 70 Библиографический список…………………………………………………….73
Предисловие Настоящее пособие предназначено для студентов первого, второго курсов направления 14040062 Электроэнергетика и электротехника при прохождении вычислительной практики. Отдельные разделы могут быть использованы в курсах «Математическое моделирование», «Переходные режимы работы электрооборудования» и т.д. Продолжительность вычислительной практики две недели. Проводится она в вычислительных центрах и вычислительных лабораториях. Распределение студентов на практику оформляется приказом по университету не позднее, чем за месяц до ее начала. Перед началом практики студенты должны получить на кафедре бланки командировочных удостоверений, пройти необходимый инструктаж. Цели и задачи вычислительной практики Основная цель вычислительной практики — это закрепление теоретических знаний, полученных в университете, и овладение практическими навыками решения конкретных задач на ЭВМ с использованием численных методов. Теоретическую основу практики составляют курсы "Информатика", "Алгоритмические языки и программирование", "Высшая математика". В задачи практики входит:
- изучение методов решения систем линейных и нелинейных уравнений, систем дифференциальных уравнений первого порядка, а также знакомство с методом наименьших квадратов; - изучение алгоритмического языка PASCAL; - составление и отладка программ для перечисленных методов на алгоритмическом языке PASCAL. Содержание практики. В период вычислительной практики каждый студент должен: - пройти на кафедре и на месте проведения практики инструктаж - ознакомиться с литературой по методам решения указанных выше задач (см. библиографический список); - изучить алгоритмический язык PASCAL для работы на компьютерах; - составить и отладить на алгоритмическом языке PASCAL программы, реализующие: 1) методы решения систем обыкновенных дифференциальных уравнений первого порядка с заданными начальными значениями; 2) методы решения систем линейных уравнений общего вида; 3) методы решения систем нелинейных уравнений; 4) аппроксимацию функции по методу наименьших квадратов, интерполяцию и сглаживание; 5) вычисление функций с помощью разложения в степенные ряды; 6) расчет переходных процессов в электрических цепях; - оценить точность полученных результатов, составить отчет по практике. Требования к отчету по практике Отчет по практике — основной документ, характеризующий работу студента во время практики. Отчет составляется каждым студентом самостоятельно, в нем должны быть отражены результаты работы, полученные практические знания и навыки, а также изученная во время практики специальная литература. Он должен быть написан грамотно и оформлен в соответствии с инструкцией. Отчет должен содержать следующие разделы: - математическая сущность используемых методов; - алгоритмы методов, указанных в индивидуальном задании студента; пояснения к блок-схемам программ и описание программ, реализующих эти методы; - индивидуальный вариант расчета; - выводы (сравнение результатов, полученных различными методами; затраты машинного времени; простота алгоритма; объем используемой памяти ЭВМ); - подробные блок-схемы программ, оформленные в соответствии с инструкцией, и распечатки программ Подведение итогов практики. В период вычислительной практики для всех студентов является обязательной ежедневная работа в вычислительной лаборатории. Студенты должны вести дневник о ежедневно выполненной работе, по которому составляется отчет. Составленный студентом отчет вместе с дневником и другими документами должен быть представлен на кафедру для проверки руководителем. После проверки материалов практики студент защищает отчет. Глава 1 Метод вращений Матрицы вращений позволяют реализовать упорядоченное исключение переменных. Построим ортогональную матрицу вращений R21 так, чтобы при левом умножении матрицы, обратной к ней, на матрицу А она обращала в ноль элемент агь (исключение переменной x1 из второго уравнения) затем матрицу R31 для обращения в ноль а и так далее, пока не будут обращены в ноль поддиагональные элементы первого столбца матрицы А:
Выполним подобную последовательность операций для всех столбцов матрицы А. Получим факторизацию, на которой основан метод вращений (Гивенса):
Схема выполнения операций
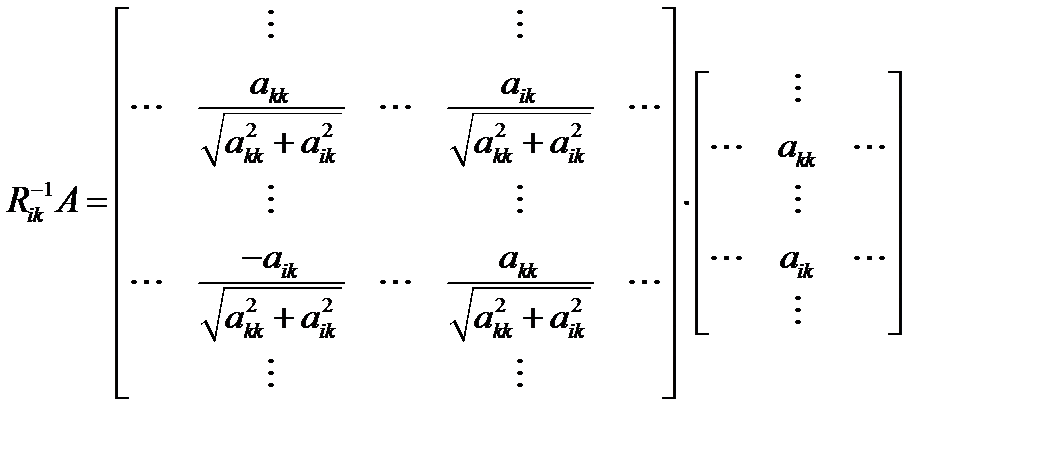
Очевидно, что в результате обратится в ноль элемент Если необходимо решить одну систему уравнений с одной правой частью, то можно использовать следующий алгоритм решения: 1) Для k=1,2,3,…, n -1 выполнить пп. 2,3,4,5. 2) Для i=k+1, k+2,…,n выполнить пп. 3,4,5. 3) Вычислить элементы c и s матрицы вращения 4) Умножить матрицу A слева на a) положить
b) для j=k+1,k+2,…,n выполнить
5) Умножить Матрицу 6) Решить полученную систему уравнений в верхней треугольной форме методом обратной подстановки. 7) Конце алгоритма. Матрица A содержит в верхнем треугольнике матрицу U, вектор B – пересчитан.
Каждый шаг исключений переменной методом вращений из очередного k-го столбца системы уравнений состоит из нескольких малых шагов, на каждом из которых необходимо строит матрицу Следует обратить внимание на то, что в отличии от метода Гаусса пересчету на кадом малом шаге подлежат так же и элементы ведущей строки В силу ортогональности матриц вращения метод является численно более устойчивым, чем метод Гаусса, однако требует в три раза больше количества операции, причем (n-1)(n-1)/2 операций вызывают функции извлечения квадратного корня. Оценка общего числа необходимых операций приближенно равна Для решения систем с различными правыми частями и одинаковой матрицей A факторизацию выполняют один раз, при этом элементы s матриц вращения запоминают на месте обращаемых в ноль элементов матрицы A. При последующих расчетах элементы c могут быть рассчитаны по формуле
Итерационное уточнение При решении линейных алгебраических систем уравнений большой размерности накапливаются ошибки округления, полученное решение может неприемлемо отличатся от точного решения. В этом случае может быть применено итерационное уточнение, под которым понимают следующий процесс:
1) Решить исходную систему уравнений 2) Вычислить вектор невязок 3) Решить систему уравнений 4) Вычислить уточненное решение 5) Повотрить пп. 2,3,4,5. 6) Конец алгоритма.
Приведенный алгоритм вытекает из следующих соотношений
Т.к. AX=B, имеем:AX=R. Следует иметь в виду, что итерационное уточнение сходится, если для матрицы A максимальное собственное число Недостатком метода итерационного уточнения является необходимость сохранения исходной матрицы А для вычисления вектора невязок, а также увеличение количества операций. Однако в ряде случаев для обеспечения точности расчета итерационное уточнение может быть полезным.
Метод Ньютона Ньютоновскими методами называют целое семейство методов, для которых собственно метод Ньютона служит базовым прототипом. Рассмотрим простой пример (рис. 1.1).
Рис. 1.1. Итерация метода Ньютона для
Поскольку dw(x0)dx можно получить новое приближение Продолжая итерационный процесс, можно с требуемой точностью риблизиться к одному из решений, например, Расчетная формула для метода Ньютона может быть получена, если представить w(x) в окрестности текущего приближения хk в виде ряда Тейлора
и ограничиться линейными членами, тогда в матричной форме получим
где Применительно к СНАУ W(X) = 0 получим следующий алгоритм: 1) Выбрать начальный вектор 2) Вычислить вектор Если к > 1 и max процесс расходится, расчет завершить аварийно. 3) Построить матрицу Якоби
и вычислить значения всех производных в точке 4) Решить систему уравнений, определив вектор поправок АХ^:
5) Вычислить новое приближение
6) Если к > ктах, где kmax — заданное предельное число итераций, то аварийно завершить расчет, иначе перейти к п. 2. 7) Конец алгоритма. Метод Ньютона при начальном приближении, близком к некоторому решению, часто обладает устойчивой квадратичной сходимостью. При плохой начальной точке В качестве косвенного критерия расходимости итерационного процесса можно использовать изменение знака якобиана — определителя матрицы Якоби. Однако это условие будучи достаточным, не является необходимым. Якобиан может быть вычислен, как побочный продукт решения методом Гаусса системы из п. 3 алгоритма.
Метод Ньютона по параметру Метод Ньютона по параметру относится к классу квазиньютоновских методов и предусматривает расчет нового исходного приближения по формуле где При Параметр Метод Бройдена предусматривает выбор параметра
В простейшем случае можно попытаться выполнить последовательность расчетов Ф(Х), уменьшая шаг вдвое, т.е. полагая Вычислим значение Ф0 и, выполнив предварительно шаг метода Ньютона, вычислим
В окрестности k-й точки производится квадратичная аппроксимация функции Ф(Х) и определяется из условия ее минимума (равенство нулю производной) значение
где Метод Матвеева предусматривает выбор оптимального параметра
Значение
где Для метода Матвеева необходимо, чтобы функции Wi были дважды дифференцируемыми по Метод Матвеева требует большего по сравнению с методом Ньютона объема вычислений и памяти, однако обладает устойчивой сходимостью при не очень хороших исходных приближениях. Доказано, что данный метод сколь угодно приближается к решению, даже если якобиан стремится к нулю, т.е. матрица Якоби очень плохо обусловлена в окрестности решения. Глава 2 Интерполяция зависимостей Интерполяция сплайнами Полиномиальная интерполяция не всегда дает удовлетворительные результаты при аппроксимации зависимостей. Так, например, при представлении полиномами резонансных кривых колебательных систем большая погрешность возникает на концах ("крыльях") этих кривых. Несмотря на выполнение условий Лагранжа в узлах, интерполяционная функция может иметь значительное отклонение от аппроксимируемой кривой между узлами. При этом повышение степени интерполяционного полинома приводит не к уменьшению, а к увеличению погрешности. Возникает так называемое явление волнистости [4]. Для проведения гладких кривых через узловые значения функции чертежники используют упругую металлическую линейку, совмещая ее с узловыми точками. Математическая теория подобной аппроксимации развита за последние тридцать лет [5, 6] и называется теорией сплайн-функций. Разработано и обширное программное обеспечение для применения сплайнов в различных областях науки и техники [7, 1]. Рассмотрим один из наиболее распространенных вариантов интерполяции кубическими сплайнами. Используя законы упругости, можно установить, что недеформируемая линейка между соседними узлами проходит по линии, удовлетворяющей уравнению
Функцию Если в качестве функции
где В отличие от полиномиальной интерполяции, когда вся аппроксимируемая зависимость описывается одним полиномом, при сплайно-вой интерполяции на каждом интервале Коэффициенты сплайнов определяются из условий сшивания соседних сплайнов в узловых точках: 1) Равенство значений сплайнов
2) Непрерывность первой и второй производных от сплайнов в узлах
Кроме перечисленных условий необходимо задать условия на концах, т.е. в точках
Для улучшения гладкости аппроксимирующей кривой используют и другие граничные условия. Например, строят так называемые нагруженные сплайны, которые в механической модели соответствуют подвешиванию грузов к металлической линейке на ее концах. Получим алгоритм определения коэффициентов кубических сплайнов из условий (2.20 — 2.24). Условия (2.20) в узлах xi-1 и x i после подстановки i -гo сплайна принимают вид ai = ƒi-1 , (2.25) ai + bi hi + cihi2 + dihi3 = ƒi ,(2.26) где hi = xi — xi- 1, 1 ≤ i ≤ n. Продифференцируем дважды сплайн (2.19) по переменной x: φ′i(x) = bi + 2ci (x— xi-1) + 3di (x— xi-1)2, (2.27) φ″i(x) = 2ci + 6di (x— xi-1). (2.28) Из условий непрерывности производных (2.21) и (2.22) при переходе в точке xiот i-го к (i1)сплайну с учетом выражений (2.27) и (2.28) получим следующие соотношения: bi + 2ci hi + 3dihi2 = bi+1 ,(2.29) ci + 3dihi = ci + 1. (2.30) И, наконец, из граничных условий (2.23) и (2.24) на основании выражения для второй производной (2.28) получим, что c1 = 0, (2.31) cn + 3dn hn = 0. (2.32) Соотношения (2.25), (2.26), (2.29) — (2.32) представляют собой полную систему линейных алгебраических уравнений относительно коэффициентов сплайнов ai, bi, ci и di. Но прежде чем решать эту систему, выгодно преобразовать ее так, чтобы неизвестными была только одна группа коэффициентов ci. Из уравнений (2.30) коэффициенты diвыразим через коэффициенты ci: ci+1 —c i di = ————. (2.33) 3 hi Объединяя уравнения (2.25) и (2.26) с уравнением (2.33), представим коэффициенты biтакже через коэффициенты ci: f i — f i-1(c i+1 + 2c i)h bi = ———— - —————. (2.34) hi 3 После подстановки выражений (2.33) и (2.34) в соотношение (2.29) получим уравнение, в которое входят только неизвестные коэффициенты ci. Для симметричности записи в полученном уравнении уменьшим значение индекса i на единицу: hi-1 ci-1+2(hi-1+hi)ci + hici+1 = 3 где 2≤ i ≤ n. При i = n, учитывая условие свободного конца сплайна, в уравнений (2.35) следует положить cn+1 = 0. (2.36) Таким образом, п — 1 уравнение вида (2.35) вместе с условиями (2.31) и (2.36) образует систему линейных алгебраических уравнений для определения коэффициентов ci. Коэффициенты d i и b i вычисляются после нахождения ci по формулам (2.33) и (2.34), коэффициенты ai равны значениям аппроксимируемой функции в узлах в соответствии с формулой (2.25). В каждое из уравнений типа (2.35) входит только три неизвестных с последовательными значениями индексов ci-1, ci, ci+1. Следовательно, матрица системы линейных алгебраических уравнений относительно ci является трехдиагональной, т.е. имеет отличные от нуля элементы только на главной и двух примыкающих к ней диагоналях. Для решения систем с трехдиагональной матрицей наиболее эффективно применять так называемый метод прогонки, являющийся частным случаем метода Гаусса. Рассмотрим алгоритм метода прогонки применительно к решаемой задаче. Для сокращения записи уравнение (2.35) представим в виде hi-1 ci-1+si ci + hici+1 = ri, (2.37) где si = 2 (hi-1 - hi ), ri = 3 Так же, как и метод Гаусса, метод прогонки разделяется на два этапа — прямой и обратный ходы. В процессе прямого хода метода прогонки вычисляют значения коэффициентов линейной связи каждого предыдущего неизвестного ci с последующим ci+1. Из уравнения (2.37) при i = 2 с учетом граничного условия (2.31) установим связь коэффициента с2 с коэффициентом с3:
c2 = k2 - l2с3, (2.39) где k2 и l2 — прогоночные коэффициенты,
. r 2 h2 k2 = —, l2 = —. S 2 S2 Затем, подставляя выражение (2.39) в уравнение (2.37) при i = 3, получим линейную связь коэффициента с3 с коэффициентом с4: c3 = k3 - l3с4, Поступая аналогичным образом для любых соседних коэффициентов с номерами i и i + 1, можно установить линейную связь в виде ci = ki - liсi+1 (2.40) В процессе выполнения прямого хода метода прогонки необходимо вычислить значения всех прогоночных коэффициентов k i и li, для которых получим рекуррентные соотношения. Подставим формулу связи (i -1)-го и i -го коэффициентов ci-1 = ki-1 - li-1сi в уравнение (2.37), в результате получим ri - hi-1ki-1hi ci = ――――― - ————— ci+1. si - hi-1li-1 si - hi-1 li-1 Сравнение последнего соотношения с формулой (2.40) позволяет записать рекуррентные соотношения для определения прогоночных коэффициентов ki и li: ri - hi-1ki-1hi ki = ――――――, li = ——————. (2.41) si - hi-1li-1 si - hi-1 - li-1
Учитывая граничное условие (2.31) и соотношение c1 = k1 - l1с2, а также полагая c2 ≠0, задаем начальные коэффициенты k1 = 0 и l1 = 0. Затем по формуле (2.41) вычислим все п пар прогоночных коэффициентов k i и li.. На основании соотношения cn = kn - l ncn+1 и граничного условия (2.36) получим, что cn = kn. (2.42) далее последовательно применим формулу (2.40) при i = n — 1, n — 2,...., 2 и вычислим значения искомых величин cn-1, cn-2,…, c2 . Эта процедура называется обратным ходом метода прогонки. Метод прогонки применяют не только для решения задач сплайн-интерполяции. Он широко используется и при численном интегрировании граничных задач для линейных дифференциальных уравнений методом конечных разностей. После определения всех коэффициентов сi другие коэффициенты сплайна вычисляются по формулам (2.25), (2.33) и (2.34). Аппроксимирующую функцию φ(x) можно рассчитать с помощью соотношения (2.19) в любой точке x на интервале [ х0, хn ]. Глава 3 Метод наименьших квадратов Общие положения Если набор экспериментальных данных получен со значительной погрешностью, то не имеет смысла использовать интерполяцию полиномами Лагранжа и сплайнами для обработки результатов. В этом случае необходимо провести аппроксимирующую кривую, которая не проходит через экспериментальные точки, но в то же время отражает исследуемую зависимость, сглаживает возможные выбросы за счет погрешности эксперимента. Обозначим узлы исходной таблицы данных через x j, где 0 ≤ j ≤ n — номер узла. Считаем известными значения экспериментальных данных в узловых точках ƒ(xj) = ƒj. Введем непрерывную функцию φ (х) для аппроксимации дискретной зависимости f(x j). В узлах функции φ (х) и f (x)будут отличаться на величину ε j = φ (x j) — - f(xj). Отклонения ε j могут принимать положительные и отрицательные значения. Чтобы не учитывать знаки, возведем каждое отклонение в квадрат и просуммируем квадраты отклонений по всем узлам: n n Q = ∑ ε j ² = ∑[φ(x j) - ƒ(x j)]² (3.1) j=0 j=0 Метод построения аппроксимирующей функции φ (х)из условия минимума величины Qполучил название метода наименьших квадратов (МНК). Наиболее распространен способ выбора функции φ (х)в виде линейной комбинации φ (х) = c0 φ 0 (x)+ c1 φ 1 (x) +... + cm φ m(x), (3.2) φ 0 (х), φ 1 (x),..., φ m (х) — базисные функции; m ≤ n; c0(x), c1 (x),.. cm (x)- коэффициенты, определяемые при минимизации величины Q. Математически условия минимума квадратов отклонений Q запишем, приравнивая к нулю частные производные от Qпо коэффициентам 0 ≤ k ≤ m: n ∂ Q⁄∂ c0 = 2∑ [c0 φ 0 (x j) + c1 φ 1(x j) +…+ j=0 + cm φ m (x j) - ƒj] φ 0 (x j) = 0, n ∂ Q⁄∂ c1 = 2∑ [c0 φ 0 (xj)+c1φ1(xj) +…+ (3.3 ) j=0 + cm φ m (x j) - ƒj] φ 1 (x j) = 0, ……………………………………. n ∂ Q⁄∂ cm = 2∑ [c0 φ 0 (x j) + c1 φ 1(x j) +…+ j=0 + cm φ m (x j) - ƒj] φ m (x j) = 0, Из системы линейных алгебраических уравнений (3.3) определяются все коэффициенты сk. Система (3.3) называется системой нормальных уравнений. Матрица этой системы имеет следующий вид:
и называется матрицей Грамма. Элементы матрицы Грамма являются скалярными произведениями базисных функций: n (φ j, φ k) = ∑ φ j (x j) φ k(x j). (3.5) j=0
Расширенная матрица системы уравнений (3.5) получится добавлением справа к матрице Грамма столбца свободных членов
где скалярные произведения, являющиеся элементами столбца, определяются аналогично (3.5):
n (φ j, ƒ) = ∑ φ j (x j) ƒ j j=0 Отметим основные особенности матрицы Грамма, полезные при программной реализации алгоритмов МНК: 1) Матрица симметрична, т.е. a i j = a j i, что позволяет сократить объем вычислений при заполнении матрицы. 2) Матрица является положительно определенной, следовательно, при решении системы нормальных уравнений методом исключения Гаусса можно отказаться от процедуры выбора главного элемента. 3) Определитель матрицы будет отличен от нуля, если в качестве базиса выбраны линейно независимые функции φk (x), при этом система (3.3) имеет единственное решение При обработке экспериментальных данных, определенных с погрешностью е в каждой узловой точке, обычно начинают с аппроксимации функцией φk (x), представимой одной-двумя базисными функциями. После определения коэффициентов ckвычисляют величину Q по формуле(3.1). Если получится, что √Q > e, то необходимо расширить базис добавлением новых функций φk (x).Расширение базиса необходимо осуществлять до тех пор, пока не выполнится условие √Q ≈ e. Выбор конкретных базисных функций зависит от свойств аппроксимируемой функции ƒ(x), таких как периодичность, экспоненциальный или логарифмический характер, свойства
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 208; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.125.2 (0.462 с.) |

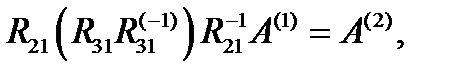 ……………………………………….
……………………………………….


 выглядит следующим образом
выглядит следующим образом .
.
 , для чего
, для чего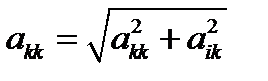

 .
. c индексами столбцов j, i, k.
c индексами столбцов j, i, k. .
. , если они не сохранены в специальных массивах данных. При решении нескольких систем с одной матрицей коэффициентов при неизвестных, но различными правыми частями общий объем вычислений сокращается.
, если они не сохранены в специальных массивах данных. При решении нескольких систем с одной матрицей коэффициентов при неизвестных, но различными правыми частями общий объем вычислений сокращается. .
. . Если все
. Если все  , где
, где  - желаемая точность, то расчет закончен и
- желаемая точность, то расчет закончен и  есть решение, иначе выполнить пп. 3,4,5.
есть решение, иначе выполнить пп. 3,4,5. относительно
относительно  - вектора итерационного уточнения.
- вектора итерационного уточнения. .
.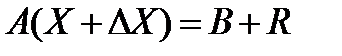 .
. сходимость может быть очень медленной, а при
сходимость может быть очень медленной, а при  процесс скорее всего расходится.
процесс скорее всего расходится.

 где
где  — начальное приближение, то
— начальное приближение, то 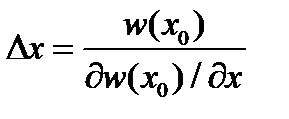 и
и .
. = 1,73205...
= 1,73205...


 положить к = 0,
положить к = 0,  =
= 
 . Если все
. Если все  <
<  , где
, где  — заданная точность расчета, то получено решение, расчет окончен..
— заданная точность расчета, то получено решение, расчет окончен.. , то итерационный
, то итерационный


 и положить к = к + 1.
и положить к = к + 1. имеет место расходящийся итерационный процесс. Метод Ньютона расходится, если матрица Якоби плохо обусловлена в окрестности решения. Часто перед использованием метода Ньютона выполняют несколько итераций, например методом последовательных приближений, для того чтобы иметь "хорошее" начальное приближение.
имеет место расходящийся итерационный процесс. Метод Ньютона расходится, если матрица Якоби плохо обусловлена в окрестности решения. Часто перед использованием метода Ньютона выполняют несколько итераций, например методом последовательных приближений, для того чтобы иметь "хорошее" начальное приближение.
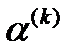 — параметр, выбираемый на каждой итерации.
— параметр, выбираемый на каждой итерации.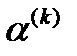 — 1 метод совпадает с обычным методом Ньютона.
— 1 метод совпадает с обычным методом Ньютона.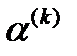 выбирают с целью ускорения сходимости и предупреждения расходимости метода. Факт расходимости может быть установлен, если невязка любого уравнения системы не уменьшилась по сравнению с предыдущей итерацией.
выбирают с целью ускорения сходимости и предупреждения расходимости метода. Факт расходимости может быть установлен, если невязка любого уравнения системы не уменьшилась по сравнению с предыдущей итерацией. в процессе поиска по направлению вектора поправок
в процессе поиска по направлению вектора поправок  минимума одной из норм вектора невязок, например, евклидовой:
минимума одной из норм вектора невязок, например, евклидовой:
 поверхности функции невязок выпуклой квадратичной функцией и выбор
поверхности функции невязок выпуклой квадратичной функцией и выбор  , обеспечивающего минимум этой функции.
, обеспечивающего минимум этой функции. Если
Если 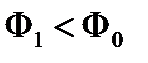 , то поиск на отрезке [0,1] начинается с а = 1, в противном случае с а = 0. Зададимся некоторым
, то поиск на отрезке [0,1] начинается с а = 1, в противном случае с а = 0. Зададимся некоторым  и вычислим значения функции Ф в точках (1 —
и вычислим значения функции Ф в точках (1 —  ) в первом случае и в точках
) в первом случае и в точках  во втором случае, где k = 1, 2,... Поиск прекращается при выполнении условия
во втором случае, где k = 1, 2,... Поиск прекращается при выполнении условия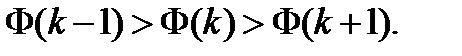
 , равное
, равное
 — точки, в которых известно значение аппроксимирующей функции
— точки, в которых известно значение аппроксимирующей функции 
 следующим образом:
следующим образом:
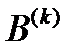 определяется, например, по следующей формуле:
определяется, например, по следующей формуле: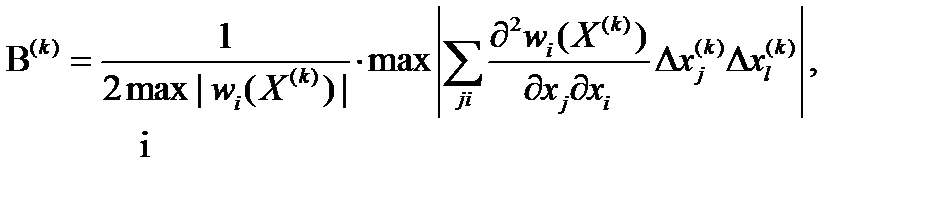
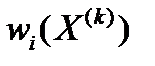 — i -e решаемое уравнение на к -й итерации, а второй сомножитель представляет собой максимальный по модулю элемент вектора-столбца, полученного умножением матрицы вторых производных системы W(X) на вектор поправок.
— i -e решаемое уравнение на к -й итерации, а второй сомножитель представляет собой максимальный по модулю элемент вектора-столбца, полученного умножением матрицы вторых производных системы W(X) на вектор поправок.
 (2.18)
(2.18) и будем использовать для аппроксимации зависимости f(x), заданной в узлах
и будем использовать для аппроксимации зависимости f(x), заданной в узлах  ,...,хп значениями
,...,хп значениями  .
. выбрать полином, то в соответствии с уравнением (2.18) степень полинома должна быть не выше третьей. Этот полином называют кубическим сплайном, который на интервале
выбрать полином, то в соответствии с уравнением (2.18) степень полинома должна быть не выше третьей. Этот полином называют кубическим сплайном, который на интервале  записывают в виде
записывают в виде (2.19)
(2.19) и
и  — коэффициенты сплайна, определяемые из дополнительных условий; i = 1,2,..., п — номер сплайна.
— коэффициенты сплайна, определяемые из дополнительных условий; i = 1,2,..., п — номер сплайна. строится отдельный полином третьей степени(2.19) со своими коэффициентами.
строится отдельный полином третьей степени(2.19) со своими коэффициентами. и аппроксимируемой функции f(x) в узлах — условия Лагранжа
и аппроксимируемой функции f(x) в узлах — условия Лагранжа (2.20)
(2.20) (2.21)
(2.21) (2.22)
(2.22) и.
и.  В общем случае эти условия зависят от конкретной задачи. Часто используют условия свободных концов сплайнов. Если линейка не закреплена в точках вне интервала [
В общем случае эти условия зависят от конкретной задачи. Часто используют условия свободных концов сплайнов. Если линейка не закреплена в точках вне интервала [  (2.23)
(2.23) - (2.24)
- (2.24) (2.35)
(2.35) . (2.38)
. (2.38) (3.4)
(3.4) ,
,


