
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поиск корней полиномиального уравнения, графическая интерпретация
Последовательность действий для нахождения корней полиномиального уравнения вида q создать вектор длиной (n +1), состоящий из коэффициентов полинома, расположенного в левой части уравнения (первый элемент - значение коэффициента полинома при х0, второй элемент - значение коэффициента полинома при х1 и т.д. и присвоить его какой-либо переменной (см. тему 2 и краткие теоретические сведения темы 6); q используя имя вектора в качестве аргумента функции polyroots, получить числовые значения корней полиномиального уравнения с помощью оператора «=». Решение системы линейных уравнений А) Последовательность действий для решения системы линейных уравнений методом Крамера такова: q создать матрицу коэффициентов системы линейных уравнений, например, q создать вектор свободных членов, например q с помощью оператора «:=» создать матрицу, равную матрице коэффициентов, например, q заменить в созданной матрице первый столбец вектором свободных членов, используя операцию выделения столбца матрицы, например, q аналогично из матрицы коэффициентов создать матрицу, в которой второй столбец заменен вектором свободных членов, затем матрицу, в которой третий столбец заменен вектором свободных членов, и т.д. (количество таких матриц определяется количеством неизвестных в системе уравнений); q найти первый корень, разделив определитель матрицы с замененным первым столбцом на определитель матрицы коэффициентов, например: q найти остальные корни системы уравнений аналогично. Б) Последовательность действий для решения системы линейных уравнений матричным методом такова: q создать матрицу коэффициентов системы линейных уравнений, например, А (см. краткие теоретические сведения темы 2); q создать вектор свободных членов системы линейных уравнений, например, B; q получить решение системы с помощью функции lsolve, параметрами которой являются матрица коэффициентов и вектор свободных членов, например: (решение также можно получить, умножив матрицу, обратную к матрице коэффициентов, на вектор свободных членов: q вывести полученный вектор, содержащий корни системы, с помощью оператора «=». Блочный метод В) Последовательность действий для решения системы линейных уравнений блочным методом такова: q задать начальные приближения для всех неизвестных, входящих в систему уравнений; q набрать ключевое слово Given; q ниже слова Given набрать уравнения, отделяя правую и левую части символом логического равенства «=» (см. краткие теоретические сведения темы 6); q набрать функцию Find, подставляя в качестве аргументов имена неизвестных системы; q вывести вектор, содержащий вычисленные значения корней, с помощью оператора «=», например Find(x1,x2,x3)=. Замечание. Корни системы уравнений, полученные разными способами, должны совпасть.
33 Аппроксимация и интерполяция данных. Основные определения Любому специалисту в своей практической деятельности приходится изучать зависимости между различными параметрами исследуемых объектов, процессов и систем. Например: зависимость числа оборотов двигателя от нагрузки, т.е. n=f(Мкр.); зависимость силы резания при обработке детали на металлорежущем станке от глубины резания, т.е. P=f(t), и т.д. Из всех способов задания зависимостей наиболее удобным является аналитический способ задания зависимости в виде функции n=f(Мкр.), P=f(t), y=f(t). Однако на практике специалист чаще всего получает зависимости между исследуемыми параметрами экспериментально. В этом случае ставится натурный эксперимент, изменяются значения параметров на входе системы, измеряются значения параметров на выходе системы. Результаты измерений заносятся в таблицу. Таким образом, в результате проведения натурного эксперимента получаем зависимости между исследуемыми параметрами в виде таблицы, т.е. получаем, так называемую, табличную функцию. Далее с этой табличной функцией необходимо вести научно-исследовательские расчеты. Например, необходимо проинтегрировать или продифференцировать табличную функцию и т.д. При такой постановке задачи моделирования нужно заменить табличную функцию аналитической. Для этой цели используются методы аппроксимации и интерполяции. Аппроксимация – это замена исходной функции f(x) функцией φ(x) так, чтобы отклонение f(x) от φ(x) в заданной области было наименьшим. Функция φ(x) называется аппроксимирующей. Если исходная функция f(x) задана таблично (дискретным набором точек), то аппроксимация называется дискретной. Если исходная функция f(x) задана аналитически (на отрезке), то аппроксимация называется непрерывной или интегральной. Интерполяция – это замена исходной функции f(x) функцией φ(x) так, чтобы φ(x) точно проходила через точки исходной функции f(x). Интерполяция еще называется точечной аппроксимацией. Точки исходной функции f(x) называются узлами интерполяции.
Экстраполяцией называется аппроксимация вне заданной области определения исходной функции, т.е.
Найдя интерполяционную функцию, мы можем вычислить ее значения между узлами интерполяции, а также определить значение функции за пределами заданного интервала (провести экстраполяцию). Основной мерой отклонения функции y(x) от функции f(x) при аппроксимации является величина, равная сумме квадратов разностей между значениями аппроксимирующей и исходной функций
Простейшими видами интерполяции является линейная и квадратичная. При линейной интерполяции точки заданной функции соединяются линейными отрезками, и функция f(x) приближается ломаной с вершинами в данных точках. В качестве уравнения интерполяционного многочлена используются уравнения прямой, проходящей через две точки. При квадратичной интерполяции в качестве приближающей функции, соединяющей соседние точки, принимается квадратный трехчлен. Такая интерполяция называется параболической. Распространенным видом интерполяции является интерполяция с использованием кубических сплайн-функций. Сплайн представляет собой модель гибкого тонкого стержня из упругого материала, закрепленного в двух соседних узлах интерполяции с заданными углами наклона α и β так, чтобы потенциальная энергия стержня была минимальна. Интерполяция может выполняться с помощью многочленов Ньютона, Эрмита, Лагранжа и т.д. Наиболее известными методами аппроксимации являются метод наименьших квадратов, метод многочленов Чебышева, рядов Тейлор и т.д. При решении задач аппроксимации часто используются функции регрессии. Регрессия – представление совокупности данных некоторой функцией f(x). Задачей регрессии является вычисление параметров функции f(x) таким образом, чтобы функция приближала последовательность исходных точек с наименьшей погрешностью. При этом функция f(x) называется уравнением регрессии. При регрессии не требуется чтобы функция проходила через все заданные точки, что особенно важно при аппроксимации данных, заведомо содержащих ошибки.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 177; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.44.207 (0.008 с.) |
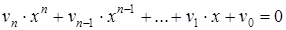 с использованием функции polyroots такова:
с использованием функции polyroots такова: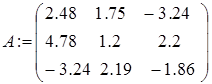 (см. краткие теоретические сведения темы 2);
(см. краткие теоретические сведения темы 2);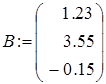 ;
; ;
; или
или  (в зависимости от значения переменной ORIGIN);
(в зависимости от значения переменной ORIGIN); ;
;
 );
);





