
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Массопередача в процессе адсорбцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основное уравнение массопередачи имеет следующий вид: M = KC F, где М —масса адсорбированного вещества; К —коэффициент массопередачи; C —средняя разность концентраций; —время; F —площадь поверхности абсорбента. При расчетах процесса адсорбции удобнее рассматривать объемный коэффициент массопередачи: КYV = М/(Y.V) где Y = Y1-Yp —движущая сила процесса, здесь Y1- концентрация влаги на входе в аппарат,кг/кг; Yp- равновесная концентрация, кг/кг; V = НS —объем адсорбента, м3, здесь Н —высота слоя, м; S —площадь сечения аппарата, м2; —порозность слоя (=0,4). Для процесса адсорбции диффузионные сопротивления внутри твердой фазы малы по сравнению с внешним диффузионным сопротивлением, поэтому, с некоторым допущением принимают КYV=YV, где YV —объемный коэффициент масоотдачи. Значение коэффициента массоотдачи YV можно определить по следующим уравнениям подобия: Для неподвижного слоя адсорбента Nu = 0,395 Re0,64 Pr0,33 для Re > 30; Nu = 0,725 Re0,47 Pr0,33 для Re = 2 — 30; Nu = 0,515 Re0,85 Pr0,33 для Re < 2; где Nu = YVd2/D —диффузионное число Нуссельта; d — эквивалентный диаметр частиц адсорбента, м; D —коэффициент диффузии; Re — число Рейнольдса (Re = 4G/(s..g); G —массовый расход паровоздушной смеси, кг/с; s —удельная поверхность зерен адсорбента, м2/м3; —динамическая вязкость паровоздушной смеси, Па.с; g —ускорение свободного падения, м/с2; Pr = /D —число Прандтля; —кинематическая вязкость. Для взвешенного слоя Nu = 46,25.10— Re1,65, где Re = wod/ —число Рейнольдса. Виды абсорбентов. 1) Пленочные (каскадные, трубчатые, насадочные) 2) Поверхностные 3) Борботажные (колокольные, тарелочные: каучуковые, сетчатые, решетчатые) 4) Растительные 5) Механические
Виды адсорбентов. Наибольшее распространение в пищевой промышленности в качестве адсорбентов нашли активированный уголь, костяной уголь, целлюлозная масса, силикагель и др. Основными характеристиками адсорбентов являются: 1. Удельная поверхность —величина поверхности приходящаяся на единицу массы или объема адсорбента; 2. Активность адсорбента —предельное количество вещества, которое может поглотить единица массы адсорбента. Адсорбенты характеризуются также плотностью, пористостью, эквивалентным диаметром гранул, гранулометрическим составом и механической прочностью. Различают истинную и, кажущуюся к и насыпную н плотность гранул. Истинная плотность и —масса единицы объема вещества из которого состоит адсорбент. Кажущаяся плотность к —отношение массы гранулы к ее объему. Насыпная плотность н —масса единицы объема слоя. Пророзность слоя адсорбента это доля объема слоя не занятая гранулами: с = 1 —(н/к). Пористость гранул это объемная доля пустот в грануле: г = 1 —(к/и). Экстракция. Процесс экстракции (извлечение) ценных веществ, входящих в состав сложного твердого тела чаще всего пористой структуры и органического происхождения, играет важную роль во многих технологических процессах различных отраслей пищевой промышленности: гидролизной, масло – жировой, сахарной, ферментной и т.д. Процесс экстракции происходит в результате непрерывного движения молекул растворителя и растворенного вещества. Чем выше температура, тем интенсивнее это движение и тем скорее произойдет выравнивание концентрации во всех точках объема, занимаемого раствором. Поэтому процесс экстракции стремятся вести при возможно более высокой температуре, которая в общем случае лимитируется технологическими соображениями. Для большей эффективности процесса важно иметь измельченное сырье, так как в этом случае увеличивается удельная (отнесенная к единице массы сырья) активная поверхность. Однако степень измельчения ограничивается гидродинамическими условиями, создающимися в том или ином аппарате. Очень маленькие частицы будут уноситься экстрагирующей жидкостью, забивать фильтрующие сита, загрязнять экстракт и т.д. Процесс, осуществляемый в экстракторах непрерывного или периодического действия, является нестандартным, так как концентрация сока в любой точке обрабатываемого материала и в движущейся экстрагирующей жидкости непрерывно изменяется во времени. Следовательно, этот процесс будет описываться сложной системой дифференциальных уравнений экстракции, уравнений движения и неразрывности потока, уравнением материального баланса, а также необходимым числом функциональных соотношений, характеризующих зависимость кинетических коэффициентов от температуры, концентрации, скорости движения и т.д. Извлечение жидкостью из пористого тела каких–то веществ, растворенных в жидкости, которая заполняет поры, определяется двумя взаимосвязанными процессами. Один из них обеспечивает подвод вещества из глубинных слоев сырья к поверхности, второй – переход этого вещества с поверхности материала в поток экстрагирующей жидкости. Интенсивность перехода вещества с поверхности частицы в поток обусловлена разностью концентраций вещества на поверхности частицы и в потоке жидкости. Обычно закон конвективного массообмена задают упрощенно в виде закона Ньютона: qп(t) = b[Cп(t) – Сс(t)], (1.1) где b - коэффициент массоотдачи, м/с; qп(t) – плотность потока вещества через время t после начала процесса с единицы поверхности частицы, (кг/м2×с); Сп(t) – концентрация растворенного вещества в поверхностном слое в момент времени t, кг/м3; Сс(t) – концентрация экстрагирующей жидкости (диффузионного сока) в данный момент времени, кг/м3. Коэффициент массоотдачи b численно равен количеству вещества, отдаваемого единицей площади в единицу времени при разности концентраций вещества на поверхности тела и в окружающей среде, равной единице. По закону сохранения массы это количество вещества должно быть равно тому его количеству, которое подводится к единице площади тела в единицу времени в результате происходящего внутри тела диффузионного процесса. Для слоев, непосредственно примыкающих к поверхностным, в соответствии с законом А. Фика можно записать:
где D1 – коэффициент массопроводности, отражающий влияние пористой структуры тела на величину коэффициента молекулярной диффузии, м2/с;
Очевидно,
Это соотношение входит в формулировку задачи в виде граничного условия третьего рода. Концентрация экстрагирующей жидкости Сс(t) будет изменяться в связи с тем, что пористое тело будет отдавать экстрагирующей жидкости извлекаемое вещество. Очевидно, величину Сс(t) можно выразить через среднеобъемную концентрацию` С(t) жидкости, находящейся в порах тела. Для противоточного процесса можно записать: V[С0 –`С (t)] = W[Ссн –`Сс (t)], (1.3) где С0 – концентрация в порах частицы при t = 0; Ссн – концентрация экстрагирующей жидкости, покидающей аппарат; V – объем жидкости, находящейся в порах единицы объема тела; W – объем экстрагирующей жидкости, приходящейся на единицу объема пористого тела. Если учесть, что в процессе экстракции будет изменяться еще V и W, то сложность решения задачи при такой постановке значительно возрастает. Задача становится еще более трудной в том случае, когда обрабатываемый материал представляет собой полидисперсную смесь, для составляющих которой среднеобъемная концентрация будет зависеть от формы и геометрических размеров частицы. Характеристикой дисперсности обрабатываемого материала может служить функция распределения характеристического размера частицы R: Ф(R) = где g – объемная или массовая доля определенной функции в полидисперсной смеси. Если тем или иным методом получено решение дифференциального уравнения с учетом соответствующих граничных и начальных условий для среднеобъемной концентрации` С(R,t) частицы размером R, то усредненная в пределах всей совокупности частиц, образующих полидисперсную смесь, концентрация может быть получена из уравнения: `С (t) = Если в полидисперсной смеси меняется и форма частиц, то решение` С(R,t) получают для той или иной формы с учетом распределения частиц, а затем с учетом объемной или массовой доли фракции определенной формы находят усредненную для всей смеси концентрацию. Для изотропного тела при отсутствии движения жидкости в порах можно записать:
где D – коэффициент диффузии, или концентрациопроводности (по аналогии с коэффициентом температуропроводности), м2/с.
В.М. Лысянский предложил интервально – итерационный метод расчета процесса диффузии, приняв гипотезу о возможности апроксимировать на каком – то небольшом участке процесса изменение концентрации экстрагирующей жидкости линейной зависимостью. Используя априорную информацию о величине коэффициентов концентрациопроводности и массоотдачи на каждом интервале, В.М. Лысянский определяет расчетную процедуру, как ряд последовательных расчетов каждого интервала. Результат расчета предыдущего интервала принимается за начальные условия для расчета последующего интервала. Этот метод позволяет при достаточно большом числе интервалов учесть зависимость кинетических коэффициентов от концентрации, температуры и других факторов. Обычно задачу еще более упрощают, полагая, во – первых, что коэффициенты D и b могут быть приняты за величины постоянные, не зависящие от концентрации и температуры, во – вторых, изменение концентрации экстрагирующей жидкости определяют из опыта, апроксимируют полученные экспериментальные данные какой – либо зависимостью и вводят соответствующую функцию в граничные условия. Некоторые авторы считают, что изменение концентрации экстрагирующей жидкости можно для некоторых экстракционных процессов описать экспоненциальной зависимостью: Сс (t) = Ссн е --kt, (1.5) где Ссн – концентрация экстрагирующей жидкости, покидающей аппарат, кг/м3; k – показатель экспоненты, 1/с; t - время, в течение которого подвергающееся обработке сырье переместится от входа в аппарат до рассматриваемой точки (сечения), с.
Для противоточного процесса, в котором частица обрабатываемого сырья может быть представлена в виде неограниченного (R3®¥) параллелепипеда, задача может быть сформулирована следующим образом:
С(x, y, 0) = Сн; (1.6)
Уравнение материального баланса можно записать в виде равенства: d`C(t)=adCc или d`C(t)= - adCcнe-ktdt (1.7) где `С(t) – среднеобъемная концентрация в твердой фазе ко времени t; a - отношение объема экстрагирующей жидкости W к объему раствора внутри материала, подвергавшегося обработке, V. Учитывая уравнение (1.7), операционным методом можно получить решение задачи (1.6) для среднеобъемной концентрации в виде бесконечного двухмерного экспоненциального ряда, быстро сходящегося для условий реального процесса. Ограничиваясь первым членом ряда, можно после ряда преобразований получить расчетное уравнение
где tк – время, необходимое для получения заданной степени извлечения Ск/Сн; С – остаточная среднеобъемная концентрация раствора внутри твердой фазы, удаляемой из аппарата. Коэффициент k определяется по следующей формуле:
Здесь Bn1, Bm1, mn1 и mm1 являютсяфункциями диффузионного критерия Био Изложенное выше свидетельствует о том, что для анализа и расчета процесса экстракции необходимо знать числовые значения коэффициентов D и b
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 779; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.109.60 (0.008 с.) |

 , (1.2)
, (1.2) - градиент концентрации у поверхности тела, кг/м4.
- градиент концентрации у поверхности тела, кг/м4.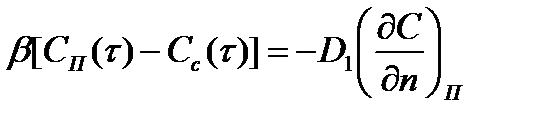 .
.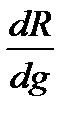 ,
, (R, t) Ф (R) dR. (1.4)
(R, t) Ф (R) dR. (1.4)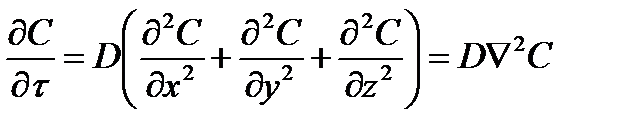 ,
, (t > 0; - R1 ³ x ³ R1; - R2 ³ y ³ R2);
(t > 0; - R1 ³ x ³ R1; - R2 ³ y ³ R2);

 , (1.8)
, (1.8) . (1.9)
. (1.9)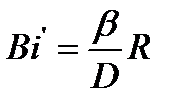 и могут быть подсчитаны по специальным формулам или взяты из соответствующих таблиц [1].
и могут быть подсчитаны по специальным формулам или взяты из соответствующих таблиц [1].


