Операція заперечення. Логічна 1. Логічне або. Виключне або.

Операція заперечення

Операція заперечення (інверсія, НЕ, NOT) є операцією над одним операндом і озна­чає, що біти із значенням “0” набувають значення “1” і навпаки. Для відображення дії ло­гічної операції часто використовують так звані таблиці істинності. Табл. 6.1 є таблицею істинності для операції заперечення.

Таблиця 6.1

біт операнда	біт результату

 

Приклади:

NOT (1000 1010 0010 1100) = 0111 0101 1101 0011.

NOT (1110 1011 1010 0111) = 0001 0100 0101 1000.

Логічне І

Ця операція (загальноприйняте позначення I, AND) передбачає наявність як міні­мум двох операндів, назвемо їх X та Y. Бона виконує порозрядну кон’юнкцію змінних, тобто отримання одиниці лише тоді, коли всі вхідні змінні рівні одиниці. Відобразимо значення функції наступною таблицею істинності (табл. 6.2.)

біт X	біт Y	біт результату

 

Приклади виконання операції логічного множення приведено на рис. 6.1.

1101 0011 0010 1110 11000101 0010 1100 0011 0010 1111 0000 1100 1101 1111 0010 = 0001 0010 0010 0000 = 1100 0101 0010 0000

Рис. 6.1. Приклади виконання операції логічного множення

Логічні АБО

Ця операція (загальноприйняте позначення АБО, ОК.) також передбачає наявність як мінімум двох операндів X та У. Вона виконує порозрядну диз’юнкцію змінних, тобто отримання одиниці тоді, коли хоча б одна вхідна змінна рівна одиниці. Відобразимо зна­чення функції наступною таблицею істинності (табл. 6.3).

Таблиця 6.3

біт X	біт Y	біт результату

 

 

Приклади виконання операції логічного додавання приведено на рис. 6.2.

1101 0011 0010 1110 1100 0101 0010 1100 0011 0010 1111 0000 1100 1101 1111 0010 = 1111 0011 1111 1110 = 1100 1101 1111 1110

Виключне АБО

Також цю операцію ще називають додавання за модулем два (XOR), оскільки вона виконує порозрядне додавання вхідних змінних за модулем два. Ця операція виконуєть­ся як мінімум над двома операндами X та Y. Відобразимо значення функції наступною таблицею істинності (табл. 6.4).

Таблиця 6.4

біт X	біт Y	біт результату

 

Рис. 6.2. Приклади виконання операції логічного додавання

Приклади виконання операції логічного додавання за модулем два наведено на рис. 6.3.

1101 0011 0010 1110 1100 01010010 1100 ¹ 0011 0010 1111 0000 1100 1101 1111 0010 = 0001 0010 0010 0000 - 1100 0101 0010 0000

Рис. 6.3. Приклади виконання операції логічного додавання за модулем два

 

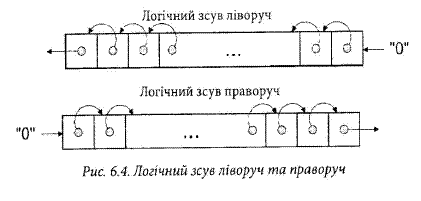
Операції зсуву.

Логічні зсуви

При виконанні логічного зсуву праворуч або ліворуч всі розряди слова зсуваються на один розряд у відповідну сторону, в перший розряд записується нуль, а останній роз­ряд випадає (рис. 6.4), Зсуви досить часто використовуються як складові операції при виконанні багатьох алгоритмів обробки даних. Для формату представлення даних без знаків зсув на один розряд ліворуч еквівалентний множенню на два, а на один розряд праворуч - відповідно цілочисельному діленню на два.

 

Команда логічного зсуву має наступні поля: код логічної операції зсуву праворуч або ліворуч, адреса операнда та код зсуву, який вказує величину зсуву, тобто кількість розрядів, на які має бути проведений зсув. Якщо операнд позначити через X, а код зсуву через У, то результат Z виконання операції буде рівним Х = Х 2^+1-y, де знак “+” відповідає зсуву ліворуч, а знак - праворуч.

Арифметичні зсуви

Арифметичні зсуви дуже подібні до попередніх (логічних), але вони мають таку особ­ливість, як розмноження знака при зсуві праворуч та збереження знака при зсуві ліво­руч (рис. 6.5).

Такі зсуви також мають зміст множення і ділення на два для формату представлення даних із знаками в оберненому та доповняльному кодах. Вони дозволяють після операції зсуву ліворуч зберегти знак представленого числа та після операції зсуву праворуч збе­регти коректний результат ділення на два.

Команда арифметичного зсуву має наступні поля: код операції арифметичного зсуву праворуч або ліворуч, адреса операнда та код зсуву, який вказує величину зсуву, тобто кількість розрядів, на які має бути проведений зсув.

Циклічні зсуви

Циклічний зсув передбачає, що розряди, які витісняються з одного боку операнда, дописуються з іншого його боку (рис. 6.6).

 

Команда циклічного зсуву має наступні поля: код операції циклічного зсуву право­руч або ліворуч, адреса операнда та код зсуву, який вказує величину зсуву, тобто кіль­кість розрядів, на які має бути проведений зсув.

 

Операції відношення.

Порівняння двійкових кодів на збіжність

Операція порівняння двійкових кодів на збіжність дає логічний результат, рівний одиниці, якщо коди збігаються. В інших випадках значення результату рівне нулю. Ви­конувана функція визначається наступним булевим рівнянням

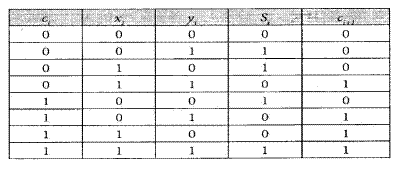
де і = 0, 1... n - номери розрядів чисел X та Y, які порівнюються, Z - розряд ре­зультату.

Визначення старшинства двійкових кодів

Операції визначення старшинства двійкових кодів, тобто визначення, яке з двох чи­сел є меншим, більшим, меншим-рівним, більшим-рівним, виконуються з використан­ням двійкового віднімання.

Якщо це числа без знаків, то при відніманні першого числа від другого отриманий результат може бути більшим нуля, рівний нулю, або меншим нуля. Тоді, якщо отрима­ний результат є більшим нуля, то перше число є більшим від другого, якщо отриманий результат рівний нулю, то числа рівні, а якщо отриманий результат є меншим нуля, то друге число є більшим від першого.

Якщо це числа із однаковими знаками, то при відніманні першого числа від другого отриманий результат може бути додатнім, рівним нулю, або від’ємним. Тоді якщо отри­маний результат рівний нулю, то числа рівні, при від’ємному результаті перше число є меншим другого, а друге відповідно більшим, а при додатному результаті перше число є більшим, а друге відповідно меншим від першого. Якщо ж це числа із різними знаками, то більшим є додатне число

Арифметичні операції.

Команди обробки даних також ініціюють виконання арифметичних операцій. Це операції додавання, віднімання, множення та ділення над числами, представленими в форматах з фіксованою та рухомою комою. При цьому арифметичні операції також мо­жуть виконуватись як над скалярними даними, так і над векторами.

До арифметичних належать також наступні операції над одиночними операндами:

■ взяття абсолютної величини від операнда;

* інверсія знака операнда;

■ прирощення операнда на одиницю;

■ зменшення операнда на одиницю.

Методи реалізації арифметичних операцій в комп’ютерах вибирають з врахуванням потрібної швидкодії, формату представлення чисел, системи числення та інших техні- ко-економічних і системних факторів. Критерієм вибору методу зазвичай є досягнен­ня мінімальних затрат обладнання, максимальної швидкодії або оптимального співвід­ношення затрат обладнання і швидкодії. Існує велика кількість алгоритмів виконання арифметичних операцій в комп’ютері. В даному розділі розглянемо лише основні алго­ритми, а питання їх модифікації та реалізації будуть розглянуті в наступних розділах.

Додавання двійкових чисел без знаків

Додавання в двійковій системі числення відбувається подібно до звичайного дода­вання в десятковій системі. Додаються два розряди, які розміщені у числі на одній по­зиції. При виникненні переносу він передається в старший розряд і там додається. В загальному додавання можна описати наступними формулами:

де: S - і-тий розряд суми, х., у. - і-ті розряди першого та другого доданків відповідно, с - розряд переносу.

Ці формули отримані з наступної таблиці істинності (табл. 6.5).

Якщо результат, який мав би бути отриманий після додавання, є більшим, ніж може вміститися в даній розрядній сітці, то старший розряд втрачається і така ситуація на­зивається втратою результату через переповнення.

Приклади виконання операції додавання двійкових чисел без знаків приведено на рис. 6.7.