
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двійкові, вісімкові та шістнадцяткові числаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
У зв’язку з тим, що елементи з двома станами використовуються як базові елементи комп’ютерної техніки, всі числа в комп’ютерах представляються у двійковій системі числення. Розглянемо особливості цієї системи. Двійкова система числення будується за тим самим правилом, що і десяткова, але в ній використовуються лише дві цифри - 0 та 1. Число у двійковій системі числення записується у вигляді: B=BN-1 BN-2…B1B0B’1B’2…B’m а значення числа обчислюється за таким виразом:
де: ■ N - кількість цифр (розрядів) у цілій частині числа (зліва від коми), ■ М - кількість розрядів у дробовій частині числа (справа від коми), ■ Bi. - значення і-го розряду (розряди цілої частини), ■ B’i. - значення і-го розряду (розряди дробової частини), ■ B - значення числа. Приклади двійкових чисел:
Часто у розробника, а то і в користувача комп’ютера, виникає потреба в перевірці коректності виконання операцій над двійковими числами комп’ютером або його вузлом. А оскільки в комп’ютерах опрацьовуються багаторозрядні двійкові числа, і оперувати з такими довгими послідовностями нулів та одиниць (наприклад, рядок із 32 цифр) незручно, то набули поширення вісімкова та шістнадцяткова системи числення. У вісімко- вій системі числення використовують вісім цифр від 0 до 7, а у шістнадцятковій системі числення крім десяткових цифр від 0 до 9 використовують 6 літер латинського алфавіту (А, В, С, Б, Е, Б) для позначення цифр від 10 до 15. Значення числа обчислюється за таким виразом:
Де: ■ N - кількість цифр (розрядів) у цілій частині числа (зліва від коми), ■ М - кількість розрядів у дробовій частині числа (справа від коми), ■ Hi. - значення і-го розряду (розряди цілої частини), ■ H’i. - значення і-го розряду (розряди дробової частини), ■ H - значення числа. ■ Особливістю цих систем є зручний перехід до двійкової системи та навпаки. Три двійкових розряди переводяться в один вісімковий, а чотири двійкових розряди - в один шістнадцятковий, як показано в табл. 2.1.
Наприклад, двійкове число 01101101 у шістнадцятковій системі записуватиметься як 60. Для переведення чисел із шістнадцяткової та вісімкової систем числення у двійкову необхідно кожну цифру числа, яке переводиться, замінити відповідно чотири- або три- розрядним двійковим еквівалентом - тетрадою або тріадою, а отримані двійкові цифри розташувати на місцях шістнадцяткових або вісімкових цифр.
У разі необхідності переведення чисел із десяткової системи числення у вісімкову, шістнадцяткову та двійкову переведення робиться лише в одну систему (вісімкову або шістнадцяткову). Подальше переведення виконується через двійкову систему, використовуючи тріади та тетради. Приклад 1. Переведемо число 12345,67 з десяткової системи числення у двійкову, вісімкову, шістнадцяткову. 1. Переведення цілої частини числа у вісімкову систему: 12345: 8 = 1543, залишок 1; 1543: 8 = 192, залишок 7; 192: 8 = 24, залишок 0; 24: 8 = 3, залишок 0; 3:8 = 0, залишок 3.
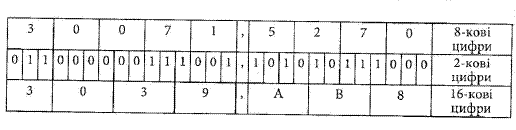
Результат: 30071. 2. Переведення дробової частини числа у вісімкову систему: 0,67x8 = 5,36; 0,36 х 8 = 2,88; 0,88 х 8 = 7,04; 0,04 х 8 = 0,32. Наближений результат: 0,5270.... 3. Отримання повного результату шляхом об’єднання результатів, отриманих в п. 1 та п. 2. Результат: 30071,5270.... 4. Переведення результату у двійкову та шістнадцяткову системи числення (табл. 2.2). Поділ двійкового числа на тріади та тетради починається від коми ліворуч і праворуч. Результат: 12345,6710=30071,52708=11000000111001,1010101112=3039,АВ816.
Переведення чисел із системи числення з основою k у десяткову систему Один із методів переведення чисел із системи числення з основою к у десяткову систему числення ґрунтується на використанні кількісного еквівалента числа. Для переведення необхідно записати число у його кількісному еквіваленті, замінивши цифри системи числення з основою к та основу к їхніми десятковими еквівалентами, а потім обчислити вираз за правилами десяткової арифметики. Приклад 1. Переведемо двійкове число 1011,1001 у десяткову систему числення. 1011,1001 = 1*23+ 0*22+1* Таким чином, 1011,10012 = 11,562510. Приклад 2. Переведемо вісімкове число 105,71 у десяткову систему числення. 105,71 = 1-82 + 0-81 + 5-8° + 7-8 1 + 1-8 2 = 64 + 0 + 5 + 0,875 + 0,015625 = 69,890625; Результат: 105,71а = 69,89062510. Приклад 3. Переведемо шістнадцяткове число 2ЕБ,0А до десяткової системи числення.
2ЕБ,0А - 2-164 14-16Ч13аб°+0-16'+10-16'2 = 512 + 224 +13+0+0,0390625 = 849,0390625; Результат: 2ЕD,0А!6 = 849,039062510.
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 434; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.23.149 (0.008 с.) |


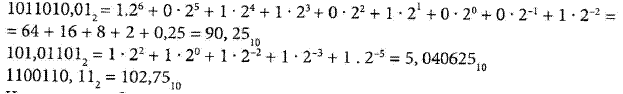

 +1*
+1*  +1*
+1* 


