Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стандарт іеее-754. Розширений двійково-кодований десятковий код обміну ebcdicСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Стандарт ІЕЕЕ-754 Для представлення чисел з рухомою комою у більшості сучасних комп’ютерів використовується стандарт ІЕЕЕ-754. В попередньому пункті ми розглянули можливі варіанти представлення даних в форматі з рухомою комою. До середини 80-х років в різних комп’ютерах використовувались різні варіанти цього представлення, що суттєво ускладнювало виконання на них тих самих програм. У 1985 році Інститут інженерів електротехніків і радіоелектроніків (ІЕЕЕ) розробив стандарт для чисел з рухомою комою, який офіційно відомий як ІЕЕЕ-754 (1985). Стандарт ІЕЕЕ-754 для чисел з одинарною точністю використовує зміщення 8-роз- рядного порядку на 127. Це ще один спосіб представлення чисел із знаком без використання знаку мінус. Мантиса має 23 біти. Із знаковим розрядом включно повна довжина слова складає 32 біти (рис. 2.13).
Значення числа обчислюється за формулою:
Мантиса представляється в прямому коді без знаку, знак мантиси представляється окремо. Суть нормалізації полягає в тому, що мантиса приводиться до вигляду І.ххххх, тобто вона знаходиться в межах від 1,000...0 до 1,111...1. Слід зауважити, що оскільки кожна мантиса після нормалізації починається з 1, то нема сенсу зберігати цей розряд, тому він не зберігається разом з числом. Його необхідно просто враховувати під час операцій над числами. Числа з подвійною точністю в стандарті ІЕЕЕ-754 подаються 64-розрядним словом, яке має знаковий розряд, 11-розрядний порядок і 52-розрядну мантису (рис. 2.14). Зміщення порядку дорівнює 1023.
Значення числа обчислюється за формулою:
У табл. 2.6 наведено характеристики форматів подання двійкових чисел в стандарті ІЕЕЕ-754 з одинарною та подвійною точністю.
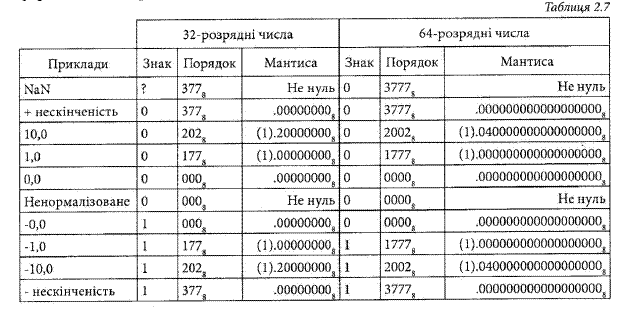
Як числа з одинарною точністю, так і числа з подвійною точністю в стандарті ІЕЕЕ- 754 мають для нуля два варіанти представлення. Коли порядок і мантиса рівні нулю - число є нулем. При цьому значення знаку є несуттєвим. На цю обставину потрібно звертати увагу при проведенні операції порівняння числа з рухомою комою на збіжність з нулем. Стандарт ІЕЕЕ-754 передбачає використання певної кількості значень мантиси та порядку для представлення нескінчених, невизначених та малих значень. Так мінус та плюс нескінченість подаїються максимальним значенням порядку (3778 для числа з оди нарною точністю та 37 778для числа з подвійною точністю) та нульовою мантисою. Для представлення невизначеного значення також використовується максимальне значення порядку та ненульова мантиса. Невизначене значення називають “не числом” - Not a Number (NaN). “Не число” використовується, щоб представити значення, яке не є дійсним числом і часто використовується як індикатор помилки, наприклад, коли відбулося ділення 0 на 0. Якщо число є дуже малим, то воно представляється нульовим порядком та ненульовою мантисою. У табл. 2.7 наведено приклади представлення різних величин в форматі за стандартом ІЕЕЕ-754 для чисел з одинарною та подвійною точністю.
Тут знаком? позначено несуттєве значення, а (1) - значення, яке не зафіксовується елементами пам’яті комп’ютера.
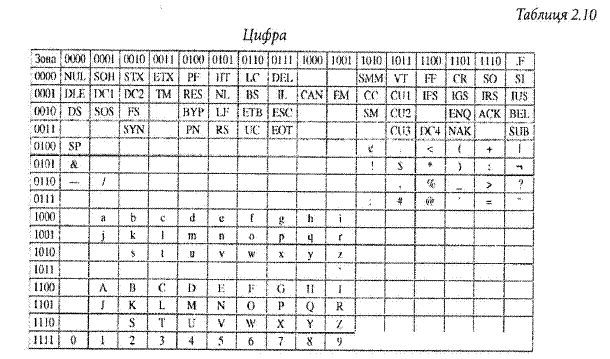
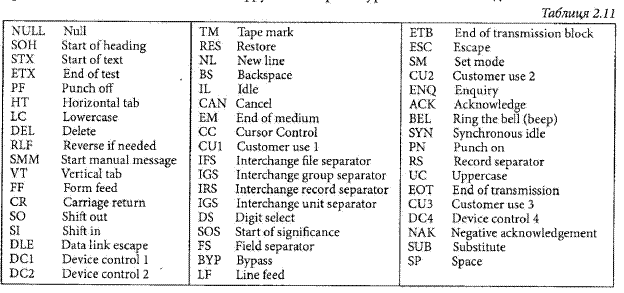
Розширений двійково-кодований десятковий код обміну EBCDIC Перед розробкою комп'ютерної системи IBM System/360, фірма IBM використала 6-розрядну версію двійково-кодованого десяткового числа для представлення символів і знаків. Цей код мав суттєві обмеження, пов’язані з малою розрядністю двійково-кодованого десяткового числа. Проектувальникам System/360 була потрібна більша інформаційна здатність коду так само як і узагальнений метод запам’ятовування і чисел, і символів. Для того, щоб підтримувати сумісність з попередніми комп’ютерами і периферійним устаткуванням, інженери IBM вирішили, що буде краще просто розширити код BCD від 5 бітів до 8 бітів. Відповідно, цей новий код було названо розширеним двійково-кодова- ним десятковим кодом обміну (EBCDIC). Фірма IBM і тепер продовжує використовувати код EBCDIC в мейнфреймах і обчислювальних системах середнього розміру. В табл. 2.10 код EBCDIC показано в зонально-цифровій формі.
Знаки представлені шляхом додавання бітів до зонних бітів. Наприклад, знаку а відповідає код 1000 0001, а цифрі 3 - код 1111 0011. Зауважимо, що єдина різниця між верхніми і нижніми символами полягає в позиції розряду 2, що дозволяє зробити перетворення від верхніх до нижніх символів (або навпаки) шляхом переключення одного двійкового розряду. Зональні біти також роблять легшою для програміста перевірку
|
|||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 474; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.115.25 (0.01 с.) |




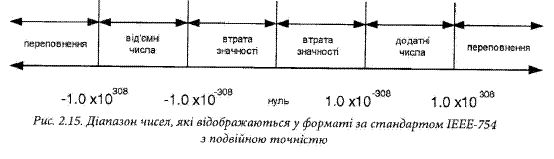
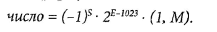 Діапазон чисел, які можуть бути представлені в цьому форматі, показаний на рис. 2.15.
Діапазон чисел, які можуть бути представлені в цьому форматі, показаний на рис. 2.15.