
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рынок труда. Функция спроса на трудСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В неоклассической модели величина совокупного предложения определяется объёмом ресурсов и используемыми в экономике технологиями. Поэтому модель совокупного предложения выводится из производственной функции (см. рисунок 1.2): Y= Y (A, L, K),
где Y – величина совокупного выпуска; А – параметр, характеризующий уровень существующей технологии; L – величина трудовых ресурсов; К – величина капитала в экономике. В экономике неоклассического типа при медленно меняющихся технологиях (А0) и величине капитала (К0) (для дальнейшего упрощения А0 и К0 принимают неизменными) производственная функция может быть представлена в виде, удобном для её графического изображения и анализа:
Наиболее широко применяемый вид производственной функции – функция Кобба-Дугласа: E = ALαKβ, где α и β – коэффициенты эластичности выпуска по труду и капиталу соответственно. Поскольку экономике неоклассического типа известна только неизменная отдача от масштаба (α + β = 1), то производственная функция Кобба–Дугласа принимает следующий вид: Y = ALαK1-α. Для неизменных технологий (А0) и запаса капитала (К0) функция – однофакторная: Y= A0L0αK1-α= ΨL0α. Таким образом, при сделанных ранее допущениях, выведение кривой совокупного предложения в неоклассической модели основывается прежде всего на анализе равновесия рынка труда. Микроэкономический анализ выбора оптимального количества труда проводится для так называемой "репрезентативной фирмы". Это некая усреднённая или типичная фирма, для которой при переходе от микроэкономического анализа к макроэкономическим выводам операция агрегирования может быть сведена к умножению. Эта фирма производит композитный товар (частичку ВВП), следовательно, y = Y/n, где n, число фирм. Поскольку Y = yn, полученные выводы будут справедливы и для макроуровня, не нужно даже менять графиков, следует лишь увеличить масштаб всех переменных в n раз. Например, график производственной функции является верным и для репрезентативной фирмы. Оптимальный объём труда фирма определяет из условия максимума прибыли MR = MC: MR = MC; => Предельный доход от труда равен MRPL = При совершенной конкуренции на рынке благ MR = Р, следовательно, MRPL = Р
MRPc = Значит, условие максимума прибыли на конкурентном рынке труда Р*МРL = W. Поскольку фирмы (и домашние хозяйства) не испытывают денежных иллюзий, то при принятии решений о величине спроса на труд (и величине его предложения) они ориентируются не на номинальную, а на реальную заработную плату (W/P). Тогда правило определения оптимальной величины спроса на труд MPL =W/P. Очевидно, что количество труда, максимизирующее прибыль фирмы, находится на пересечении кривой MPL и горизонтальной линии, проведённой на уровне (W/P)1. Повышение реальной платы за труд с (W/P)1 до (W/P)2 приведёт к снижению привлекаемого фирмой количества этого ресурса с L1 до L2. Уменьшение платы за труд увеличивает спрос на его количество. Таким образом, в неоклассической модели кривая предельного продукта (MPL)устанавливает однозначное соответствие между величиной спроса на труд и ставкой реальной заработной платы и является одновременно и кривой спроса фирмы на труд Ld (рисунок 1.3).
Следовательно, рыночный спрос на труд (Ld) отрицательно зависит от реальной заработной платы и представлен функцией
Ld = Ld(W / P).
Отрицательный наклон рыночной кривой спроса на труд определяется убыванием предельного продукта труда (MPL) с ростом занятости. Спрос на труд повышается (кривая Ld сдвигается вправо) если: 1) увеличивается совокупный спрос на продукцию фирм (и соответственно растёт и уровень цен); 2) увеличивается предельная производительность труда (MPL). Рост предельной производительности труда может быть следствием, например, увеличения запаса капитала в экономике или совершенствования применяемой технологии. Условие максимизации прибыли в самом общем виде можно записать: MPL = ∂Y/∂L = YL' = W/P.
|
|||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 2981; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.82.108 (0.011 с.) |


 Y = f(A0, L,K0) Y = Y(L).
Y = f(A0, L,K0) Y = Y(L). =
= 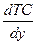 ; =>
; =>  =
=  =
=  ; => MRPL = MPCL.
; => MRPL = MPCL. MPL на рынке же труда
MPL на рынке же труда  предельные издержки на труд
предельные издержки на труд = W.
= W.



