Модель трансакционного спроса на деньги баумоля – Тобина

Эмпирические наблюдения болеё поздних лет побудили амери­каннского исследователя, лауреата Нобелевской премии Джеймса Тобина и известного английского экономиста Вильяма Баумоля неза­висимо друг от друга показать, что возможность выгодного вложе­ния средств способна повлиять на решение экономических субъек­тов относительно объёма активных денежных запасов.

Данная модель получила название модели трансакционного спроса на деньги Баумоля – Тобина. Она обрела огромную популяр­ность, так как её проверка уже несколько десятилетий даёт очень хорошие ретроспективные и прогнозные результаты.

Предпосылки модели трансакционного спроса на деньги Баумо­ля – Тобина:

1) домохозяйство получает номинальный доход в размере I один раз в период, равный t;

2) доход I тратится равномерно и концу периода t оказывается израсходованным;

3) деньги переводятся на сберегательный счёт, против которого нельзя выписывать чеки;

4) по остаткам на сберегательном счёте начисляется процент­ный доход по ставке процента i¹;

5) каждый раз за снятие денег со счёта берётся фиксированная плата, а издержки одного посещения банка, которые включают рас­ходы на транспорт, потери времени на проезд, стояние в очереди и пр. (так называемые «издержки на подмётки»), равны F.

Пусть сначала домохозяйство сразу снимает все деньги, посту­пившие на сберегательный счёт (рисунок 7.2). Тогда в начальный момент его денежный запас равен всей сум­ме доходаm_H = I, а на конец периода он уменьшается до нуля т_k = 0. Величина денежных средств на депозите за период t равна нулю (D_H = D_k =0).

 

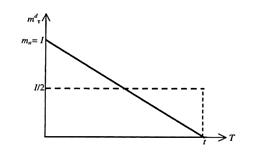
Рисунок 7.2 – Динамика трансакционных кассовых остатков домашнего хозяйства

во времени при однократном посещении банка

 

Тогда в среднем величина трансакционных кассовых остатков домашнего хозяйства за период t будет составлять половину дохода:

m^d_T =(m_H + m_k) /2 = I/2.

Если, например, ежемесячный доход домохозяйства составляет 10 000 руб. и он сразу снимается со сберегательного счёта, то запас денег (а значит, и величина трансакционногоспроса на деньги) в среднем равняется 5 000 руб.

Получение наличных денег со счёта сопровождается издержка­ми двух видов.

Во-первых, это фиксированные издержки одного посещения банка, равные F¹. В общем случае затраты на конвертацию доход­ных финансовых активов в наличные деньги называются трансакционными издержками. Трансакционные издержки хранения наличных денег в данном случае – это издержки посещения банка и затраты на снятие денег с банковского счёта. Пусть они равны F = 20 руб.

Во-вторых, альтернативные издержки хранения наличных денег (так как на кассовые остатки на руках процент не начисляется, то хранение запаса наличных денег ведёт к потерям в виде неполучен­ного процентного дохода, которые, следовательно, являются неяв­ными). Альтернативные издержки хранения денежного запаса – это издержки, равные неполученному процентному доходу по храня­щимся в наличной форме деньгам.

Если ежемесячная ставка процента по остаткам на сберегатель­ном счёте в нашем примере i = 1%, то домохозяйство, сразу же снявшее со счёта всю сумму в 10 000 руб., упустило возможность получить процентный доход в размере 100 руб.(10 000 х 0,01). Этот упущенный доход и представляет собой альтернативные издержки (издержки упущенных возможностей) хранения денег ТС_а =100 руб.

Таким образом, суммарные издержки хранения трансакционного запаса денег в размере 5 000 руб. составляют:

ТС=F+ТС_а == 100+ 20 =120 руб.

Пусть домохозяйство, осознав нерациональность своего первоначального решения, снимает не все, а только половину денег, поступивших на его сберегательный счёт (рисунок 7.3). Тогда на начало периода t его денежный запас равен половине номинального дохода т_H = //2, а в конце периода он уменьшается до нуля т_k = 0. Следовательно, в среднем величина трансакционных кассовых остатков домашнего хозяйства за период, равный t, теперь будет составлять только четверть дохода: m^d_T =(m_H + m_k) /2 = (I/2+0)/2 = I/4. Следовательно, и величина трансакционного спроса на деньги в нашем примере уменьшится до 2 500 руб. Хранение запаса наличных денег в размере I/4 ведёт к потерям в виде неполученного процентного дохода, т.е. сопровождается аль­тернативными издержками в размере: ТС а = I/4 • i. Альтернативные издержки хранения денежного запаса при дву­кратном посещении банка уменьшаются (в нашем примере со 100 до 50 руб.). Трансакционные издержки при этом, напротив, увеличатся до 2F = 40 руб. Суммарные издержки хранения трансакционного запаса денег в размере 2 500 руб. составляют: ТС = 2F + ТС_а= 40 + + 50 = 90 руб.

Таким образом, перед рационально хозяйствующим субъектом встаёт проблема, какую часть номинального дохода хранить в лик­видной форме, а какую держать в виде финансовых активов (в на­шем случае на сберегательном счёте) в целях получения процентно­го дохода?

Домохозяйство должно выбрать такой объём трансакционных денежных запасов, который минимизирует издержки, связанные с хранением этих запасов. Величина и трансакционных, и альтернатив­ных издержек зависит в нашем случае от числа походов в банк (п). Поэтому решение проблемы сводится к определению количест­ва посещений банка, минимизирующего суммарные издержки.

Величина трансакционных издержек хранения кассовых остат­ков в рассматриваемом варианте модели Баумоля – Тобина в общем случае равна Fn. Когда количество посещений банка равно и денежный запас на начало периода составляет m_H= IIп. В конце периода t он уменьша­ется до нуля m_k= 0 (рисунок 7.3).

 

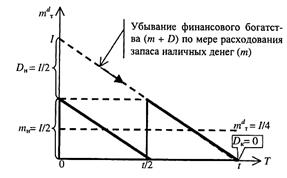
Рисунок 7.3 – Динамика трансакционных кассовых остатков домашнего хозяйства во времени при двукратном посещении банка

 

В среднем величина трансакционных кассовых остатков (вели­чина трансакционного спроса на деньги) домашнего хозяйства за период, равный t, будет равняться

m^d_T =(m_H + m_k) /2 = (I/n +0)/2 = I/2n.

Хранение запаса наличных денег такой величины сопровожда­ется альтернативными издержками (неполученным процентным до­ходом): ТСа= I/2n • i. Суммарные издержки хранения трансакционного запаса денег при n посещениях банка составят: TC = nF+ ТС_а = nF + I/2n• i.

 

Величина издержек хранения запаса наличных денег – функция нескольких переменных (n, F, I, i). Необходимое условие минимума функции: дTC/дn = F – (I • i)/2n² = 0. Откуда оптимальное число посещений банка, минимизирующеё общие издержки владения наличными деньгами: n* = √(I • i)/2F. Достаточное условие минимума функции д²TC/дn² =(I • i)/n³ > 0 выполняется при любом значении n (рисунок 7.4).

 

Рисунок 7.4 – Графический способ нахождения оптимального числа посещений банка

Подставив найденное число посещений банка в формулу, опре­деляющую кассовые остатки, получим функцию индивидуального трансакционного спроса на деньги (рисунок 2.14):

m^d_T = I/2n = √(I • F)/2i.

Рисунок 7.5 – Индивидуальный спрос на трансакционные кассовые остатки

Анализ функции спроса на трансакционные кассовые остатки приводит к выводам:

1) величина трансакционного спроса на деньги отрицательным образом зависит от ставки процента и положительным – от дохода и транснакционных издержек.

2) при формировании спроса на трансакционные кассовые ос­татки в модели Баумоля – Тобина нет денежных иллюзий. При росте уровня цен, например в z раз, во столько же раз вырастут I и F, а следовательно, и спрос на деньги.

Спрос на реальные кассовые ос­татки не изменится.