
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема 1. Для подобных явлений можно составить безразмерные сочетания параметров, имеющих одинаковые значения в сравниваемых явлениях.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Эти сочетания параметров называются критериями подобия. Теорема 2 (π -теорема). Всякое уравне-ние, описывающее какой-либо физический процесс и записанное размерным образом в определенной системе единиц, можно преобразовать в безразмерное уравнение, состоящее из критериев подобия π. Пусть в уравнение входит m величин и пусть k из них независимы друг от друга. Тогда полученное уравнение для независимых критериев будет иметь вид f(π1, π2, …. πm-k) = 0. Если его разрешить относительно критерия π1 = Ф(π2, π3,…. πm-k), то отсюда видно, что из всевозможно составленных критериев подобия независимыми будут только m – k – 1 критериев. Теорема 3. Подобие процессов осуществляется при пропорциональности всех сходственных в них параметров и при равенстве m – k – 1 критериев подобия, определенных согласно теореме 2. Если в рассматриваемых физических явлениях или системах существует равенство не всех, а лишь некоторых независимых критериев подобия, то говорят о неполном, или частичном, подобии. При этом важно, чтобы влияние критериев, равенство которых не соблюдается, было незначительно или малосущественно на протекание рассматриваемых физических процессов. – (См. Моделирование, Критерии подобия). Теплоёмкость – количество теплоты, поглощаемой телом при нагревании на 1 градус (1˚ С или 1К). Теплоёмкость единицы массы вещества называется удельной теплоёмкостью (единица измерения Дж/(кг∙К)), теплоёмкость 1 моля вещества называется молярной (единица измерения Дж/(моль∙К)). Количество теплоты, поглощаемой телом при нагревании, и теплоёмкость тела зависят от способа нагревания. Различают теплоёмкость при постоянном объёме Теплообмен – самопроизвольный необратимый процесс переноса теплоты, обусловленный градиентом температуры. Различают следующие виды теплообмена: теплопроводность, конвекция, лучистый теплообмен, теплообмен при фазовых превращениях.
Теплопроводность – один из видов переноса теплоты от более нагретых частей тела к менее нагретым, приводящий к выравниванию температуры. При теплопроводности перенос энергии осуществляется в результате непосредственной передачи энергии от частиц (молекул, атомов), обладающих большей энергией, частицам с меньшей энергией. Основной закон теплопроводности – закон Фурье: плотность теплового потока Теплота - форма проявления внутренней энергии тела без совершения работы. Теплота может быть преобразована в другие виды энергии. Теплота фазового перехода – количество теплоты, которое нужно сообщить веществу (или отвести от него) при равновесном изобарно-изотермическом переходе вещества из одной фазы в другую (фазовом переходе 1-го рода - кипении, плавлении, кристаллизации, полиморфном превращении и т.п.). Существование теплоты фазового перехода физически обусловлено различием энергии связи вещества в соответствующих фазах. Различают удельную и молярную теплоту фазового перехода, отнесённые соответственно к 1 кг и 1 молю вещества. Для фазовых переходов 2-го рода теплота фазового перехода равна нулю. Термодинамика – наука о наиболее общих свойствах макроскопических тел. В термодинамике изучаются макроскопические системы, состоящие из большого числа частиц, причём исследуются наиболее общие свойства таких систем, для описания которых не требуется привлечения микроскопических характеристик системы. Равновесное состояние термодинамической системы однозначно определяется несколькими термодинамическими параметрами (См. Параметры состояния). Три начала термодинамики являются основой, на которой строится её теоретический аппарат (См. Первое начало термодинамики, Второе начало термодинамики, теорема Нёрнста).
Термодинамическая система - совокупность физических тел, которые могут взаимодействовать между собой и с другими телами (внешней средой) - обмениваться с ними энергией и веществом. Термодинамическая система состоит из столь большого числа структурных частиц (атомов, молекул), что ее состояние можно характеризовать макроскопическими параметрами: давлением, плотностью, концентрацией веществ, образующих термодинамическую систему и др. Термодинамическая система находится в равновесии, если параметры системы с течением времени не меняются и в системе нет каких-либо стационарных потоков (вещества, теплоты и др.). Для равновесных систем вводится понятие температуры как параметра состояния, имеющего одинаковое значение для всех макроскопических частей системы. Число независимых параметров состояния равно числу степеней свободы термодинамической системы, остальные параметры могут быть выражены через независимые с помощью уравнения состояния. В термодинамике рассматривают следующие виды термодинамических систем: закрытые – не обмениваются веществом с другими системами; открытые – обмениваются веществом и энергией с другими системами; адиабатные – отсутствует теплообмен с другими системами; изолированные – не обмениваются с другими системами ни энергией, ни веществом. Для термодинамических систем выполняются законы термодинамики. Термодинамические параметры (параметры состояния) - температура, плотность, давление, объем, удельное электрическое сопротивление и другие физические величины: - однозначно определяющие термодинамическое состояние системы; - не учитывающие молекулярное строение тел; Термодинамические потенциалы – функции определённого набора термодинамических параметров (температуры
Термодинамический процесс - всякое изменение, происходящее в термодинамической системе и связанное с изменением хотя бы одного ее параметра состояния. Термодинамическое равновесие термодина-мической системы (тепловое равновесие) – состояние термодинамической системы, в которое она самопроизвольно приходит через достаточно большой промежуток времени в условиях изоляции от окружающей среды. При термодинамическом равновесии в системе прекращаются все необратимые процессы, связанные с диссипацией энергии: теплопроводность, диффузия и др. В состоянии термодинамического равновесия макроскопические параметры системы с течением времени не меняются. При этом внутри равновесной системы продолжаются микроскопические процессы: изменяются положения молекул и их скорости при столкновениях. В состоянии термодинамического равновесия энтропия системы максимальна.
Термодинамическое состояние – равновесное макроскопическое состояние термодинамической системы, которое фиксируется заданием параметров состояния, представляющих собойизмеряемые макроскопическими приборами средние величины определенного набора характеристик системы. Конкретный набор этих параметров определяется тем, каким способом рассматриваемая равновесная система выделяется из среды окружающих её тел и других систем. Техническая атмосфера – внесистемная единица давления: равна 1 кгс/см2 = 9,80665 Н/см2. 1 ат = 98066,5 Па. Техническая атмосфера – внесистемная единица давления: равна 1 кгс/см2 = 9,80665 Н/см2. 1ат = 98066,5 Па. Толщина вытеснения δ * – величина, используемая в современной теории пограничного слоя для характеристики его толщины, которая вычисляется более точно, чем физическая толщина пограничного слоя δ: δ * = где Толщина вытеснения представляет собой отклонение линий тока вязкой жидкости от линий тока идеальной жидкости, которое вызвано образованием пограничного слоя. Толщина потери импульса δ ** – величина, характеризующая толщину пограничного слоя, определяется уравнением: δ ** = где Траектория – кривая, которую описывает радиус – вектор r = r (t) координат жидкой частицы с течением времени. Уравнение траектории можно записать в координатной форме: Трубка Вентури (расходомер Вентури) – устройство для замера расхода или скорости жидкостей и газов в трубопроводах. Представляет собой плавное сужение на трубопроводе, где скорость возрастает, а давление соответственно уменьшается. За сужением трубопровод снова плавно расширяется, образуя диффузор, где происходит обратный переход кинетической энергии потока в энергию давления. Обозначим через
Трубка Пито – прибор для измерения динамического (полного) давления Трубка Пито – Прандтля – комбинированная трубка для измерения полного (динамического) Трубка тока – поверхность, образованная линиями тока, проходящими через все точки замкнутого контура, не являющегося линией тока, внутри движущейся жидкости. Касательные к линиям тока совпадают с направлением скоростей движения частиц жидкости, находящихся на этих линиях. При неустановившемся движении жидкости линии тока меняются от момента к моменту, поэтому трубка тока тоже меняет свою форму. При установившемся движении жидкости линии тока совпадают с траекториями частиц и остаются неизменными; в этом случае трубка тока сходна с трубкой с твердыми стенками, внутри которой происходит течение жидкости с постоянным расходом через сечение трубки. Трубопровод – устройство или сооружение из плотно соединенных труб, предназначенное для транс-портировки жидких, газообразных или сыпучих веществ. В зависимости от транспортируемой среды для трубопроводов используются термины: водопроводы, газопроводы, паропроводы, нефтепроводы, воздухопроводы, маслопроводы, молокопровод и т.д. Турбулентное течение ( от лат. Turbulentus - беспорядочный) - течение жидкости или газа, при котором вследствие наличия в течении многочисленных вихрей различных размеров жидкие частицы совершают неупорядоченные, хаотические, неустановившиеся движения по сложным траекториям, а скорость, температура, давление и плотность среды испытывают хаотические изменения. Турбулентное течение отличается от ламинарного течения интенсивным перемешиванием, распределением осреднённой скорости по сечению потока, зависимостью коэффициента сопротивления от числа Турбулентное течение наблюдается при достаточно больших числах Рейнольдса в трубах, каналах, пограничных слоях при обтекнии поверхностей твёрдых тел, в следах за обтекаемыми телами, струях, зонах перемешивания между потоками с разными скоростями, в каналах энергетических машин, в разнообрахных природных условиях.
Мгновенные скорости, давления, плотности среды при турбулентных режимах испытавают с течением времени хаотические изменения, пульсируют. Поэтому для описания турбулентного течения используют усреднённые по времени скорости и давления. Местная усреднённая скорость
Разность векторов
Аналогичным образом производится усреднение давлений: Для описания усреднённо установившегося турбулентного течения несжимаемой жидкости используются уравнения Рейнольдса, которые получаются из уравнений Навье – Стокса, все члены которых усредняют по времени. Турбулентное течение в круглых трубах: Расчет турбулентного течения в трубах относится к широко распространенным инженерным задачам. Для турбулентного течения характерно перемешивание жидкости, пульсации скоростей и давлений. Линии тока в прямолинейной трубе при турбулентном течении не являются прямыми. Турбулентное течение всегда является неустойчивым, т.к. значения скоростей и давлений меняются с течением времени. Если осредненные значения скоростей и давлений с течением времени не изменяются, то течение можно считать установившимся.
Рис.4. Профили скоростей при ламинарном и тубулентном течении в трубе: Re1 ≤ Re2 ≤ Re3
Распределение осредненных по времени скоростей по сечению в турбулентном потоке отличается от ламинарного. Профиль скоростей для турбулентного потока более наполненный, Важным элементом расчета является нахождение закона распределения осредненных скоростей в поперечном сечении трубы. Наиболее распространенной является эмпирическая степенная зависимость вида
где - зависимость показателя степени от числа - ограниченный диапазон изменения числа - дает неверные значения градиента скорости у стенки и на оси трубы (производная от скорости на оси трубы не равна нулю). Для приближенного расчета турбулентного течения в трубе можно использовать двухслойную модель течения, состоящую из тонкого вязкого ламинарного подслоя и центральной части потока – турбулентного ядра, в котором преобладают турбулентные напряжения, т.е.
где
Подставив (3) в (2) и интегрируя, получим для основной части турбулентного потока логарифмический закон распределения скоростей
где
Касательные напряжения на стенке
где Для расчета гидравлических потерь при турбулентном течении в трубах необходимы данные о зависимости коэффициента гидравлического трения от числа Re и относительной шероховатости. Используя полуэмпирическую теорию, для гладкостенного режима течения при 4000 ≤ Re ≤ 20 Никурадзе был получен следующий закон распределения скоростей
Положив в этой формуле Используя логарифмический закон распределения скоростей (7), Никурадзе для гладких труб была получена следующая зависимость для гидравлического коэффициента трения (формула Никурадзе для гладких труб):
Преимуществами этой формулы являются ее теоретическая обоснованность, однозначная зависимость коэффициента гидравлического трения от числа Re, хорошее совпадение с экспериментом. Недостаток формулы – неявное выражение λ в функции Re. В технических расчетах чаще используют другие полуэмпирические и эмпирические формулы. Для зоны гладкостенного течения применяют формулу Блязиуса
и формулу Конакова
Для зоны квадратичного сопротивления Никурадзе на основе полуэмпирической теории была получена формула (формула Никурадзе для шероховатых труб)
Для зоны квадратичного сопротивления часто применяют формулу Шифринсона
А.Д.Альтшуль рассматривал турбулентное течение как единое целое, не выделяя в нем вязкий подслой и учитывая не только турбулентные, но и вязкостные напряжения. Им для коэффициента гидравлического трения получена формула, применяемая для всех трех зон турбулентного течения
Недостаток формулы – неявное выражение λ в функции Re. Из формулы Альтшуля как частные случаи получаются формулы Никурадзе.
Используя некоторые допущения, Альтшуль получил приближенную формулу, дающую достаточно точные результаты во всех трех зонах турбулентного течения
Если трубы достаточно гладкие, т.е. Если трубы шероховатые, т.е.
Рис. 5. Зависимость потерь на трение от режима течения
В турбулентном потоке при Re › Reкр потери энергии на трение по длине значительно больше, чем в ламинарном (Рис. 5). При ламинарном течении потери на трение пропорциональны скорости в первой степени, а при переходе к турбулентному течению заметен скачок сопротивления и более крутое нарастание величины hтр по кривой, близкой к параболе. Турбулентность – сложное, неупорядоченное во времени и пространстве поведение диссипативной среды, детали которого не могут быть воспроизведены на больших интервалах времени при сколь угодно точном задании начальных и граничных условий. Такая невоспроизводимость есть следствие собственной сложной динамики среды, определяемая неустойчивостью индивидуальных движений частиц. У Угловая скорость вращения частицы жидкости ω – векторная величина, характеризующая быстроту вращения частицы жидкости вокруг оси, проходящей через её полюс:
где Угол атаки – угол между направлением скорости поступательно движущегося тела и каким-нибудь характерным направлением, связанным с телом (у крыла самолета – с хордой крыла; у снаряда, ракеты – с их осью симметрии). Ударная адиабата (адиабата Гюгонио) - кривая, изображающая уравнение Гюгонио. Ударная волна (скачок уплотнения) – распространяющаяся со сверхзвуковой скоростью поверхность разрыва непрерывности скорости течения, давления, плотности и других величин (тонкая переходная область, в которой происходит резкое увеличение плотности, давления и скорости вещества). Ударные волны возникают при взрывах, детонации, мощных электрических разрядах, при сверхзвуковых движениях тел. Толщина фронта ударной волны имеет порядок длины свободного пробега молекулы, однако при многих теоретических исследованиях с большой точностью заменяют фронт ударной волны поверхностью разрыва, считая, что при прохождении через неё параметры меняются скачком. Неподвижную ударную волну называют скачком уплотнения. Пусть ударная волна возникает в цилиндрической трубе постоянного сечения. При переходе потока через ударную волну должны выполняться законы сохранения массы, импульса и энергии. Поэтому параметры потока перед (обозначены индексом 1) и за ударной волной (обозначены индексом 2) связаны между собой соотношениями Ренкина - Гюгонио:
Удельный объем – объем, занимаемый единицей массы вещества; величина, обратная плотности: v=1/ρ. Уравнение Бернулли(интеграл Бернулли) – одно из основных уравнений гидромеханики. При установившемся движении несжимаемой идеальной жидкости в однородном поле силы тяжести имеет вид: gh + p/ρ + c2/2=const, где с – скорость жидкости, p – давление в ней, ρ – ее плотность, h – высота частицы над некоторой горизонтальной плоскостью, g – ускорение свободного падения. Уравнение Бернулли выражает для движущейся жидкости закон сохранения механической энергии и устанавливает зависимость между c, p и h. Уравнение Ван-дер-Ваальса - уравнение состояния реального газа, учитывающее взаимодействие между молекулами газа и собственный объем молекул. Для газа, содержащего
где Уравнение Громеки–Лэмба – уравнение движения вязкой несжимаемой жидкости – одна из форм уравнения Навье–Стокса:
где
где
Уравнение Гюгонио 2 (P.H.Hugoniot) – устанавливает связь между давлением и плотностью газа по обе стороны скачка уплотнения:
где
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 570; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.211.49 (0.016 с.) |

 и теплоёмкость при постоянном давлении
и теплоёмкость при постоянном давлении  , если в процессе нагревания поддерживаются постоянными соответственно объём тела или давление. Для идеальных газов разность молярных теплоёмкостей
, если в процессе нагревания поддерживаются постоянными соответственно объём тела или давление. Для идеальных газов разность молярных теплоёмкостей  где
где 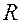 =8,31 Дж/(моль∙К) – универсальная газовая постоянная. У жидкостей и твёрдых тел разница между
=8,31 Дж/(моль∙К) – универсальная газовая постоянная. У жидкостей и твёрдых тел разница между 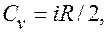 где
где  – число степеней свободы молекулы.
– число степеней свободы молекулы. (количество теплоты, которое переносится в единицу времени через единицу площади) прямо пропорциональна градиенту температуры
(количество теплоты, которое переносится в единицу времени через единицу площади) прямо пропорциональна градиенту температуры  :
:  , где
, где  – коэффициент теплопроводности.
– коэффициент теплопроводности.  где
где  – плотность газа,
– плотность газа,  – удельная теплоёмкость при постоянном объёме,
– удельная теплоёмкость при постоянном объёме, 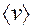 – средняя арифметическая скорость движения молекул,
– средняя арифметическая скорость движения молекул,  – средняя длина свободного пробега.
– средняя длина свободного пробега. , давления
, давления  энтропии
энтропии  и др.), характеризующих состояние макроскопической термодинамической системы, позволяющие найти все термодинамические характеристики системы как функции этих параметров. К потенциалам термодинамическим относятся внутренняя энергия
и др.), характеризующих состояние макроскопической термодинамической системы, позволяющие найти все термодинамические характеристики системы как функции этих параметров. К потенциалам термодинамическим относятся внутренняя энергия 
 (изохорно-изоэнтропийный потенциал), энтальпия
(изохорно-изоэнтропийный потенциал), энтальпия  (изобарно-изоэнтропийный потенциал), Гельмгольца энергия
(изобарно-изоэнтропийный потенциал), Гельмгольца энергия  (изохорно-изотермический потенциал), Гиббса энергия
(изохорно-изотермический потенциал), Гиббса энергия  (изобарно-изотермический потенциал). Все термодинамические потенциалы связаны между собой соотношениями:
(изобарно-изотермический потенциал). Все термодинамические потенциалы связаны между собой соотношениями: 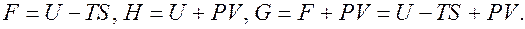 Зная термодинамические потенциалы как функции указанных параметров, по любому из них с помощью дифференцирования по его параметрам можно найти все остальные параметры, характеризующие систему:
Зная термодинамические потенциалы как функции указанных параметров, по любому из них с помощью дифференцирования по его параметрам можно найти все остальные параметры, характеризующие систему: ;
;
 ,
, - скорость жидкости в сечении пограничного слоя,
- скорость жидкости в сечении пограничного слоя, 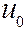 - скорость внешнего потока.
- скорость внешнего потока.

 Принимая во внимание, что скорость
Принимая во внимание, что скорость 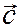 жидкой частицы направлена по касатетельной к траектории, элементарное перемещение жидкой частицы d r за время dt равно dr = c dt. Поэтому уравнение траектории можно представить в следующем виде:
жидкой частицы направлена по касатетельной к траектории, элементарное перемещение жидкой частицы d r за время dt равно dr = c dt. Поэтому уравнение траектории можно представить в следующем виде:  где
где  – проекции d r на оси координат, а
– проекции d r на оси координат, а 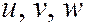 – проекции вектора скорости c на оси координат. При установившееся течении жидкости траектории совпадают с линиями тока.
– проекции вектора скорости c на оси координат. При установившееся течении жидкости траектории совпадают с линиями тока.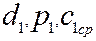 и
и  диаметр, давление и среднюю скорость соответственно во входном 1 и в самом узком 2 сечениях трубки Вентури. Тогда для несжимаемой жидкости плотностью
диаметр, давление и среднюю скорость соответственно во входном 1 и в самом узком 2 сечениях трубки Вентури. Тогда для несжимаемой жидкости плотностью  разность давлений определяется соотношением
разность давлений определяется соотношением  По измеренной разности давлений и размерам трубки Вентури из последнего равенства можно найти среднюю скорость потока в сечении 1, а следовательно, и расход
По измеренной разности давлений и размерам трубки Вентури из последнего равенства можно найти среднюю скорость потока в сечении 1, а следовательно, и расход  , где
, где  – площадь поперечного сечения трубопровода,
– площадь поперечного сечения трубопровода,  – коэффициент расхода трубки Вентури. Трубки Вентури применяют для измерения расхода жидкостей и газов в трубопроводах.
– коэффициент расхода трубки Вентури. Трубки Вентури применяют для измерения расхода жидкостей и газов в трубопроводах. текущей жидкости, представляющий собой Г-образно изогнутую трубку, отверстие которой расположено перпендикулярно линиям тока жидкости, а противоположное колено ориентировано вертикально. Полное давление реализуется при изоэнтропическом торможении потока до нулевой скорости. Высота столба жидкости в вертикальном колене прямо пропорциональна динамическому напору.
текущей жидкости, представляющий собой Г-образно изогнутую трубку, отверстие которой расположено перпендикулярно линиям тока жидкости, а противоположное колено ориентировано вертикально. Полное давление реализуется при изоэнтропическом торможении потока до нулевой скорости. Высота столба жидкости в вертикальном колене прямо пропорциональна динамическому напору. давлений в потоке. От трубки Пито отличается наличием отверстий на боковой поверхности трубки для измерения статического давления в потоке
давлений в потоке. От трубки Пито отличается наличием отверстий на боковой поверхности трубки для измерения статического давления в потоке  Зная
Зная  потока в данной точке на основании уравнения Бернулли:
потока в данной точке на основании уравнения Бернулли:  где
где  , гораздо большей интенсивностью тепло- и массообмена.
, гораздо большей интенсивностью тепло- и массообмена. где
где 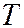 – период усреднения,
– период усреднения,  – произвольный момент времени. Интервал
– произвольный момент времени. Интервал  Проекции вектора усреднённой скорости на оси координат:
Проекции вектора усреднённой скорости на оси координат:


 .
. и
и 




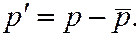 Если усреднённые параметры от времени не зависят, турбулентное течение называют усреднённо установившимся или просто установившимся.
Если усреднённые параметры от времени не зависят, турбулентное течение называют усреднённо установившимся или просто установившимся.
 (1)
(1)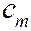 ─ скорость на оси трубы,
─ скорость на оси трубы,  - координата, отсчитанная от стенки трубы в направлении оси. С ростом числа
- координата, отсчитанная от стенки трубы в направлении оси. С ростом числа  т. Воспользовавшись полуэмпирической теорией Прандтля, можно рассчитать профиль осредненных скоростей в турбулентном ядре потока. По формуле Прандтля турбулентные напряжения
т. Воспользовавшись полуэмпирической теорией Прандтля, можно рассчитать профиль осредненных скоростей в турбулентном ядре потока. По формуле Прандтля турбулентные напряжения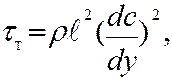
 - длина пути перемешивания. По Прандтлю,
- длина пути перемешивания. По Прандтлю,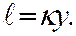 (3)
(3)
 , (4)
, (4) ─ касательные напряжения на стенке трубы. При турбулентном течении в трубе касательные напряжения распределяются по линейному закону
─ касательные напряжения на стенке трубы. При турбулентном течении в трубе касательные напряжения распределяются по линейному закону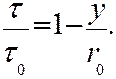 (5)
(5)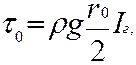 (6)
(6) ─ гидравлический уклон.
─ гидравлический уклон.
 (7)
(7) можно получить значение максимальной скорости на оси трубы
можно получить значение максимальной скорости на оси трубы  .
.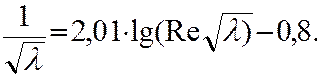 (8)
(8) (9)
(9) (10)
(10)
 (11)
(11) (12)
(12) (13)
(13)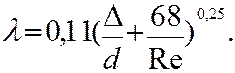 (14)
(14) <<
<<  то (14) совпадает с формулой Блязиуса (9).
то (14) совпадает с формулой Блязиуса (9).

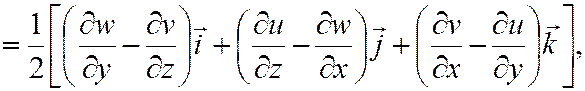
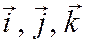 – единичные векторы. В случае потенциального течения жидкости
– единичные векторы. В случае потенциального течения жидкости 
 – закон сохранения массы;
– закон сохранения массы; – закон сохранения импульса;
– закон сохранения импульса;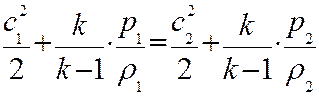 – закон сохранения энергии, где
– закон сохранения энергии, где  – отношение удельных теплоемкостей газа при постоянном давлении и постоянном объеме. Кроме того, при переходе через скачок уплотнения не изменяется газовая постоянная:
– отношение удельных теплоемкостей газа при постоянном давлении и постоянном объеме. Кроме того, при переходе через скачок уплотнения не изменяется газовая постоянная: где
где  - газовая постоянная. Уравнение Гюгонио устанавливает связь между давлением и плотностью по обе стороны скачка уплотнения. (См. также Ударная адиабата).
- газовая постоянная. Уравнение Гюгонио устанавливает связь между давлением и плотностью по обе стороны скачка уплотнения. (См. также Ударная адиабата). молей, уравнение Ван-дер-Ваальса имеет вид:
молей, уравнение Ван-дер-Ваальса имеет вид: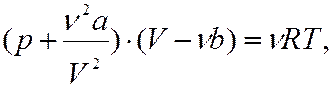
 - объем;
- объем; 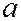 и
и  - экспериментальные константы, учитывающие притяжение и отталкивание молекул. Член
- экспериментальные константы, учитывающие притяжение и отталкивание молекул. Член  учитывает притяжение молекул газа в результате межмолекулярного взаимодействия, константа
учитывает притяжение молекул газа в результате межмолекулярного взаимодействия, константа 

 – напряжение массовых сил,
– напряжение массовых сил,  Если массовые силы обладают потенциалом, то
Если массовые силы обладают потенциалом, то  где
где  - потенциал массовых сил. В этом случае уравнение Громеки–Лэмба приводится к виду:
- потенциал массовых сил. В этом случае уравнение Громеки–Лэмба приводится к виду:
 – удельная энергия единицы объема жидкости. С учетом этого уравнение Громеки–Лэмба принимает вид:
– удельная энергия единицы объема жидкости. С учетом этого уравнение Громеки–Лэмба принимает вид:

 – давление газа до и после скачка уплотнения;
– давление газа до и после скачка уплотнения;  – плотность газа до и после скачка уплотнения,
– плотность газа до и после скачка уплотнения,  – отношение теплоёмкостей при постоянном давлении и постоянном объёме. Уравнение Гюгонио представляет собой адиабату, отличную от изоэнтропической адиабаты Пуассона; эту адиабату называют ударной адиабатой или адиабатой Гюгонио. Уравнение Гюгонио можно представить и в таком виде:
– отношение теплоёмкостей при постоянном давлении и постоянном объёме. Уравнение Гюгонио представляет собой адиабату, отличную от изоэнтропической адиабаты Пуассона; эту адиабату называют ударной адиабатой или адиабатой Гюгонио. Уравнение Гюгонио можно представить и в таком виде:



