
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь между числами маха до и после скачка имеет видСодержание книги
Поиск на нашем сайте
Температуры адиабатически аторможенного газа перед и за скачком одинаковы: Переход через скачок уплотнения не является изоэнтропийным процессом и сопровождается необратимыми преобразованиями механической энергии в тепловую, при этом энтропия возрастает. Изменение энтропии при переходе через скачок уплотнения определяется формулой:
где Скоростной напор (динамическое давление)– кинетическая энергия единицы объёма идеальной несжимаемой жидкости: Скорость звука – скорость распространения малых возмущений в жидкости или газе. Для баротропной жидкости скорость звука Смачивание – процессы, происходящие при взаимодействии жидкости с поверхностью твёрдого тела или другой жидкости и проявляющиеся в растекании жидкости и формировании площади адгезионного контакта, возникновении менисков в капиллярных каналах, образовании капель жидкости на поверхности или пузырьков в жидкости, в проникновении жидкости в капиллярно-пористые тела. Смачивание – следствие адгезии жидкости к определённой поверхности. Мерой смачивания считают краевой угол Совершенный газ – в гидроаэромеханике – газ, параметры которого удовлетворяют уравнению Клапейрона-Менделеева
Солитон – структурно устойчивое локализованное возмущение однородной или пространственно-периодической нелинейной среды, распространяющееся в виде волны без деформации профиля (например, цунами в океане). Солитоны ведут себя подобно частицам: при взаимодействии друг с другом или другими возмущениями они не разрушаются, а расходятся, сохраняя свою структуру; могут образовывать связанные состояния, ансамбли. Сообщающиеся сосуды – сосуды, имеющие в нижней части соединительные каналы. Если капиллярными явлениями можно пренебречь, то в сообщающихся сосудах свободные поверхности покоящейся жидкости находятся на одном уровне. Сопло – канал переменного по длине поперечного сечения, предназначенный для разгона жидкостей или газов до заданной скорости и придания потоку заданного направления. В сопле происходит непрерывное увеличение скорости жидкости или газа в направлении течения от начального значения на входе в сопло до наибольшей скорости на выходе из сопла. При движении по соплу внутренняя энергия рабочего тела преобразуется в кинетическую энергию вытекающей струи. Одновременно с ростом скорости в сопле происходит непрерывное падение давления и температуры от их начальных значений на входе до наименьших значений в выходном сечении сопла. Из уравнения Гюгонио 1 следует, что в случае изоэнтропийного энергетически изолированного течения газа дозвуковой поток ( Статистическая физика – раздел физики, выражающий свойства макроскопических систем, состоящих из очень большого числа одинаковых частиц (молекул, атомов, электронов и т.д.) через свойства этих частиц и взаимодействие между ними.
Статистический вес (термодинамическая вероятность)в термодинамике и статистической физике – число способов, которыми может быть реализовано данное макроскопическое состояние системы. Статистический вес Стационарное состояние в термодинамике – состояние, в котором термодинамические параметры системы не зависят от времени. Стационарные состояния могут быть как равновесными (см. Равновесие термодинамическое), так и неравновесными в зависимости от граничных условий, накладываемых на систему. Неравновесные стационарные состояния возможны лишь в открытых термодинамических системах. Стокса закон – закон, определяющий силу сопротивления Струя – 1). Часть жидкости, ограниченная по-верхностью траекторий, проведенных через каждую точку замкнутого контура, проведенного в жидкости. При стационарном течении струя совпадает с трубкой тока. Форма течения жидкости, при которой жидкость (газ) течет в окружающем пространстве, заполненном жидкостью (газом) с отличающимися от струи параметрами. В приближенной модели течения идеальной жидкости граница струи является поверхностью тангенциального разрыва, и вещество струи не смешивается с веществом окружающего пространства. В реальных течениях ввиду неустойчивости тангенциального разрыва между струей и окружающим её внешним пространством возникает слой вязкого перемешивания, в котором все параметры течения изменяются непрерывно от соответствующих струе до соответствующих окружающему внешнему пространству. Сублимация (возгонка) – переход вещества из твердого агрегатного состояния в газообразное. Т Текучесть – свойство жидкостей и газов вязко деформироваться под действием напряжений; проявляется при любых напряжениях, характеризуется величиной, обратной вязкости. У газов механизм текучести связан с переносом импульса из тех слоёв, где имеется преобладающее движение молекул газа в направлении течения, к слоям, у которых это движение меньше. У жидкостей механизм текучести представляет собой преобладающую диффузию в направлении действия напряжений. Температура – физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. В состоянии термодинамического равновесия все тела, образующие систему, имеют одинаковую температуру. Если изолированная система не находится в равновесии, то с течением времени температуры всех тел выравниваются – наступает термодинамическое равновесие (первый постулат, или нулевое начало термодинамики). В равновесных условиях температура пропорциональна средней кинетической энергии Е поступательного движения частиц тела: Е
Температура кипения – температура равновесного перехода жидкости в пар при постоянном внешнем давлении (фазовый переход 1-го рода). Температура плавления – температура равновесного перехода кристаллического (твёрдого) вещества в жидкость при постоянном внешнем давлении (фазовый переход 1-го рода). Тензор напряжений – симметричный тензор 2-го ранга, состоящий из девяти величин, представляющих напряжения в произвольной точке жидкости или газа, характеризует напряженное состояние среды в этой точке: P = Компоненты тензора Тензор скоростей деформаций – симметричный тензор второго ранга, определяется таблицей Компоненты тензора Теорема Гельмгольца (первая) – См. основная теорема кинематики жидкости. Теорема Гельмгольца (вторая): поток вектора вихря скорости через произвольное сечение вихревой трубки в данный момент времени одинаков вдоль всей трубки: Теоре́ма Жуко́вского — теорема о подъёмной силе, действующей на тел о, обтекаемое плоскопараллельным потоком идеальной несжимаемой жидкости или газа: Подъемная сила крыла бесконечного размаха равна произведению плотности газа (жидкости), скорости газа (жидкости), циркуляции скорости потока и длины выделенного отрезка крыла. Направление действия подъемной силы получается поворотом вектора скорости набегающего потока на прямой угол против циркуляции: F =ρc∞ F — подъёмная сила, ρ — плотность жидкости, c∞ — скорость потока жидкости на бесконечности, Г — циркуляция скорости (вектор направлен перпендикулярно плоскости профиля, направление вектора зависит от направления циркуляции),
Физически возникновение циркуляции связано с наличием вязкости и образованием вихрей при обтекании тела реальной жидкостью. Жуковский ввёл в идеальной жидкости условный, присоединённый к твёрдому телу вихрь, интенсивность которого равна циркуляции Г по замкнутому контуру, окружающему обтекаемый профиль. Величина Г может быть найдена на основании постулата Чаплыгина – Жуковского. Теорема Жуковского легла в основу теории крыла и гребного винта. С помощью теоремы Жуковского можно вычислить подъёмную силу крыла конечного размаха, тягу гребного винта, силу давления на лопатку турбины или компрессора и др. Теорема Нернста (третье начало термодинамики) – теорема термодинамики, согласно которой энтропия любой системы стремится к конечному пределу, не зависящему от давления, плотности или фазы, при стремлении температуры к абсолютному нулю (формулировка Нернста). М.Планк сформулировал третье начало термодинамики следующим образом: при стремлении абсолютной температуры к нулю энтропия любого тела стремится к нулю.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 737; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.178.241 (0.01 с.) |


 Особенностью ударной адиабаты является то, что при увеличении
Особенностью ударной адиабаты является то, что при увеличении  отношение плотностей
отношение плотностей  асимптотически приближается к пределу, равному
асимптотически приближается к пределу, равному  . Это значит, что как бы ни возрастало давление при переходе через скачок уплотнения, возрастание плотности не может превосходить этого предела.
. Это значит, что как бы ни возрастало давление при переходе через скачок уплотнения, возрастание плотности не может превосходить этого предела.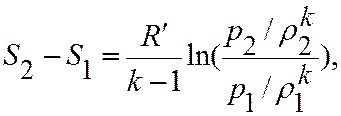
 - газовая постоянная.
- газовая постоянная. , где
, где  - плотность жидкости,
- плотность жидкости,  - скорость её течения; входит составной частью в уравнение Бернулли. Измеряется с помощью трубки Пито – Прандтля.
- скорость её течения; входит составной частью в уравнение Бернулли. Измеряется с помощью трубки Пито – Прандтля.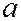 определяется следующей зависимостью:
определяется следующей зависимостью:  , где
, где  – давление в среде,
– давление в среде,  (м/с), где
(м/с), где  – отношение теплоемкости газа при постоянном давлении к теплоемкости при постоянной температуре,
– отношение теплоемкости газа при постоянном давлении к теплоемкости при постоянной температуре, 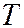 – абсолютная температура. Для воздуха
– абсолютная температура. Для воздуха  (м/с). Для продуктов сгорания
(м/с). Для продуктов сгорания  (м/с).
(м/с). , отсчитываемый от смачиваемой поверхности в сторону смачивающей жидкости:
, отсчитываемый от смачиваемой поверхности в сторону смачивающей жидкости:  где
где  – коэффициенты поверхностного натяжения на границах: твёрдое тело – газ, твёрдое тело – жидкость, жидкость – газ.
– коэффициенты поверхностного натяжения на границах: твёрдое тело – газ, твёрдое тело – жидкость, жидкость – газ. , где
, где  < 1) ускоряется в суживающемся сопле (площадь поперечного сечения сопла уменьшается в направлении течения газа), а сверхзвуковой (
< 1) ускоряется в суживающемся сопле (площадь поперечного сечения сопла уменьшается в направлении течения газа), а сверхзвуковой (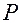 равен числу микроскопических состояний, реализующих данное макроскопическое состояние. Статистический вес связан с энтропией
равен числу микроскопических состояний, реализующих данное макроскопическое состояние. Статистический вес связан с энтропией  системы соотношением Больцмана
системы соотношением Больцмана  , где
, где  – постоянная Больцмана.
– постоянная Больцмана. , испытываемую твёрдым шаром при его медленном равномерном поступательном движении в неограниченной вязкой жидкости:
, испытываемую твёрдым шаром при его медленном равномерном поступательном движении в неограниченной вязкой жидкости:  где
где  – коэффициент вязкости жидкости,
– коэффициент вязкости жидкости,  – радиус шара,
– радиус шара,  – скорость его поступательного движения.
– скорость его поступательного движения. , где
, где  по энтропии
по энтропии  Такая температура всегда положительна, и её называют абсолютной температурой. За единицу температуры в СИ принят кельвин (К).
Такая температура всегда положительна, и её называют абсолютной температурой. За единицу температуры в СИ принят кельвин (К). .
.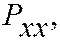


 , стоящие по главной диагонали, представляют собой нормальные напряжения; а компоненты
, стоящие по главной диагонали, представляют собой нормальные напряжения; а компоненты  =
= 

 представляют
представляют  где
где  .
. представляют собой скорости относительных линейных деформаций жидких отрезков в направлении соответствующих координатных осей, а компоненты
представляют собой скорости относительных линейных деформаций жидких отрезков в направлении соответствующих координатных осей, а компоненты  – скорости угловых деформаций (деформации сдвига) жидкой частицы в соответствующих координатных плоскостях.
– скорости угловых деформаций (деформации сдвига) жидкой частицы в соответствующих координатных плоскостях. Эту величину принимают за количественную характеристику вихревого движения и называют интенсивностью или напряжённостью вихревой трубки
Эту величину принимают за количественную характеристику вихревого движения и называют интенсивностью или напряжённостью вихревой трубки  .
. Г, где
Г, где 


