
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
При изотермическом процессе работа газаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
где При адиабатическом расширении работа газа может быть определена по одной из следующих формул:
где Равновесие термодинамическое – состояние термодинамической системы, в которое она самопроизвольно приходит через достаточно большой промежуток времени в условиях изоляции от окружающей среды. При термодинамическом равновесии в системе прекращаются все необратимые процессы, связанные с диссипацией энергии: теплопроводность, диффузия и др. Одно из условий термодинамического равновесия системы – равновесие механическое. В отсутствие внешних полей и вращения системы условием её механического равновесия является постоянство давления во всём объёме системы. В состоянии термодинамического равновесия параметры системы не меняются со временем. В состоянии термодинамического равновесия энтропия системы максимальна. Равновесный процесс – процесс перехода термодинамической системы из одного равновесного состояния в другое, столь медленный, что все промежуточные состояния можно рассматривать как равновесные, т.е. характеризующиеся очень медленным (в пределе - бесконечно медленным) изменением термодинамических параметров состояния. Всякий равновесный процесс является обратимым процессом (см.) и, наоборот, любой обратимый процесс является равновесным. Равнораспределения энергии по степеням свободы закон – утверждение, согласно которому в классической равновесной статистической системе средняя кинетическая энергия, приходящаяся на каждую поступательную (трансляционную), вращательную и колебательную степени свободы, а также потенциальная энергия, приходящаяся на каждое гармоническое колебание в системе, равны Расход объёмный (м3/с) через поперечное сечение потока жидкости площадью
Расход массовый Уравнение расхода для газа можно записать, используя газодинамическую функцию
где
Тогда Уравнение расхода газа можно выразить через газодинамическую функцию
где
Реальные жидкости - жидкости, обладающие: Реальный газ - газ, свойства которого зависят от взаимодействия молекул между собой. Потенциальная энергия взаимодействия частиц реального газа сравнима с их кинетической энергией. Реология – наука о деформациях и течении реальных сплошных сред (неньютоновских жидкостей, дисперсных систем, обладающих пластичностью). Росы точка – температура, до которой должен охладиться воздух, чтобы находящийся в нём водяной пар достиг состояния насыщения (при данной влажности воздуха и неизменном давлении). При достижении точки росы в воздухе начинается конденсация водяного пара. С Сверхзвуковое течение – течение газа, в котором в рассматриваемой области скорости Сжимаемость – способность жидкости (или газа) изменять свой объем (или плотность) под действием всестороннего давления. Величину сжимаемости характеризует изотермический коэффициент сжимаемости
где Величина, обратная изотермическому коэффициенту сжимаемости, называется модулем упругости жидкости:
Выражение Скачок уплотнения – характерная для сверхзвукового течения газа узкая область, в которой происходит резкое уменьшение скорости газа (от сверхзвуковой до дозвуковой) и соответствующий рост давления, температуры, плотности и энтропии газа. Скачок уплотнения в некоторых случаях тождествен ударной волне, а в других случаях составляет часть её структуры. Толщина скачка уплотнения мала – порядка средней длины свободного пробега молекулы, поэтому в большинстве задач газовой динамики толщиной скачка уплотнения пренебрегают. Различают прямой скачок уплотнения, в котором не происходит изменения направления вектора скорости, и косой скачок уплотнения, в котором вектор скорости поворачивается на некоторый угол. Скачок уплотнения прямой – поверхность разрыва параметров, нормальная к скорости невозмущённого потока; при переходе через прямой скачок уплотнения направление течения не изменяется. Прямые скачки уплотнения возникают при сверхзвуковом обтекании тупых углов, а также при некоторых условиях в сверхзвуковых струях и соплах. Уравнения динамической совместимости для прямого скачка уплотнения имеют вид: - уравнение сохранения массы: - уравнение изменения количества движения:
- уравнение энергии:
где Для прямого скачка уплотнения в результате решения уравнений сохранения массы, энергии и количества движения и уравнения состояния газа можно получить следующие соотношения, связывающие параметры газа перед скачком уплотнения (обозначены индексом 1) с параметрами газа за скачком уплотнения (обозначены индексом 2):
где
Соотношение давлений, температур и плотностей перед и за скачком уплотнения можно выразить через число Маха - соотношение давлений:
- соотношение температур:
- соотношение плотностей:
Скорости газа до и после скачка уплотнения связаны соотношениями:
|
||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 695; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.151.127 (0.012 с.) |


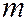 – масса газа,
– масса газа,  – газовая постоянная,
– газовая постоянная, 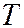 – температура,
– температура,  и
и  – начальное и конечное давление газа.
– начальное и конечное давление газа.
 ;
; ,
, – удельная теплоёмкость газа при постоянном объёме,
– удельная теплоёмкость газа при постоянном объёме,  – показатель адиабаты,
– показатель адиабаты, 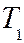 и
и  - температура газа в начале и конце расширения.
- температура газа в начале и конце расширения. где
где  – постоянная Больцмана,
– постоянная Больцмана,  – температура. Таким образом, на каждую колебательную степень свободы приходится энергия в 2 раза больше, чем на каждую поступательную и вращательную.
– температура. Таким образом, на каждую колебательную степень свободы приходится энергия в 2 раза больше, чем на каждую поступательную и вращательную. представляет собой поток вектора скорости
представляет собой поток вектора скорости 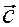 через это сечение и определяется уравнением
через это сечение и определяется уравнением  где
где  – проекция вектора скорости на нормаль к элементарной площадке
– проекция вектора скорости на нормаль к элементарной площадке 
 (кг/с) через конечное сечение площадью
(кг/с) через конечное сечение площадью  где
где  – плотность жидкости.
– плотность жидкости. - приведенную плотность тока (см.):
- приведенную плотность тока (см.): ,
, – полное давление (давление торможения),
– полное давление (давление торможения), 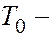 температура торможения,
температура торможения, 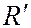 – газовая постоянная,
– газовая постоянная,  – показатель адиабаты. Обозначим постоянные, зависящие от рода газа, через
– показатель адиабаты. Обозначим постоянные, зависящие от рода газа, через


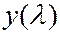 - приведенный статический импульс (см.):
- приведенный статический импульс (см.):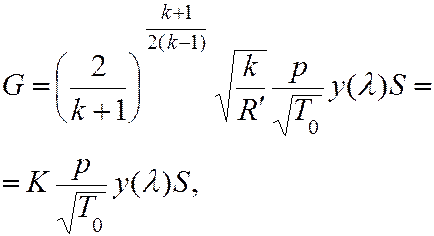
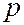 – давление.
– давление. его частиц больше местных значений скорости звука
его частиц больше местных значений скорости звука 


 - плотность жидкости (газа),
- плотность жидкости (газа),  - давление,
- давление, 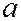 - скорость звука в среде. У жидкостей с ростом температуры изотермический коэффициент сжимаемости растет, с ростом давления – уменьшается. Для идеального (совершенного) газа изотермический коэффициент сжимаемости
- скорость звука в среде. У жидкостей с ростом температуры изотермический коэффициент сжимаемости растет, с ростом давления – уменьшается. Для идеального (совершенного) газа изотермический коэффициент сжимаемости  Для газов в качестве критерия сжимаемости употребляют число Маха М; если М < 0,2, газ можно считать несжимаемой жидкостью.
Для газов в качестве критерия сжимаемости употребляют число Маха М; если М < 0,2, газ можно считать несжимаемой жидкостью. . Для идеального газа модуль упругости равен давлению:
. Для идеального газа модуль упругости равен давлению: 
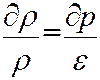 представляет собой закон Гука для жидкости.
представляет собой закон Гука для жидкости.
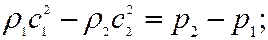

 - энтальпия; индексами 1 и 2 обозначены параметрыгаза перед и за скачком уплотнения соответственно,
- энтальпия; индексами 1 и 2 обозначены параметрыгаза перед и за скачком уплотнения соответственно, 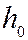 - энтальпия торможения.
- энтальпия торможения. 
 или
или 
 - отношение теплоемкостей при постояном давлении и постоянном объеме. Эти соотношения получили название ударной адиабаты, или адиабаты Гюгонио. Её можно представить и в другом виде:
- отношение теплоемкостей при постояном давлении и постоянном объеме. Эти соотношения получили название ударной адиабаты, или адиабаты Гюгонио. Её можно представить и в другом виде:
 и безразмерную скорость
и безразмерную скорость 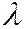 :
:


 или
или  где
где  - критическая скорость,
- критическая скорость, 


