
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение функции тока также сводится к решению уравнения Лапласа с учетом соответствующих граничных условий (задача Дирихле).Содержание книги
Поиск на нашем сайте
Для плоскопараллельного потенциального течения несжимаемой жидкости потенциал скорости в комбинации с функцией тока составляют комплексный потенциал Потенциалы термодинамические – функции определённого набора термодинамических параметров (температуры
Поток жидкости - движение массы жидкости, ограниченной системой поверхностей твердых тел и/или поверхностей соприкосновения жидких и газообразных тел. Приведенная скорость (скоростной коэффициент, коэффициент скорости)
где Присоединенная масса – фиктивная масса, которая присоединяется к массе движущегося в жидкости тела для количественной характеристики инерции окружающей его жидкой среды, для учета воздействия среды на это тело. При неустановившемся поступательном движении тела в идеальной жидкости возникает сопротивление жидкости, пропорциональное ускорению движения тела и обусловленное увлечением среды, окружающей тело; коэффициент пропорциональности и представляет собой присоединенную массу. Если присоединить к телу, движущемуся в жидкости дополнительную (присоединенную) массу, равную массе жидкости, увлекаемой телом, то закон его движения в жидкости будет таким же, как в пустоте. Значение присоединенной массы зависит от формы тела, направления движения и плотности среды.
Присоединенный вихрь – условный вихрь, неподвижно связанный с телом (крылом), обтекаемым безвихревым потоком идеальной жидкости или газа. Он заменяет по величине циркуляции скорости ту действительную завихренность, которая образуется в пограничном слое вследствие вязкости. Интенсивность присоединенного вихря (циркуляция вектора скорости по контуру, охватывающему крыловой профиль) определяется на основе постулата Чаплыгина-Жуковского. Пуазейля закон – закон установившегося течения вязкой несжимаемой жидкости в тонкой цилиндрической трубке круглого сечения, согласно которому секундный объёмный расход Пуазейля течение – ламинарное течение жидкости через тонкие цилиндрические трубки (см. Пуазейля закон). Р Работа при изменении объема газа - работа, совершаемая газом при расширении или сжатии против сил внешнего давления. Если газ расширяется, то он совершает положительную работу. Если газ сжимается, то он совершает отрицательную работу. Элементарная работа при расширении газа
|
|||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.156.84 (0.01 с.) |

 являющийся функцией от комплексного переменного
являющийся функцией от комплексного переменного 
 , объёма
, объёма  , давления
, давления  энтропии
энтропии  и др.), характеризующих состояние макроскопической термодинамической системы, позволяющие найти все термодинамические характеристики системы как функции этих параметров. К потенциалам термодинамическим относятся внутренняя энергия
и др.), характеризующих состояние макроскопической термодинамической системы, позволяющие найти все термодинамические характеристики системы как функции этих параметров. К потенциалам термодинамическим относятся внутренняя энергия 
 (изохорно-изоэнтропийный потенциал), энтальпия
(изохорно-изоэнтропийный потенциал), энтальпия  (изобарно-изоэнтропийный потенциал), Гельмгольца энергия
(изобарно-изоэнтропийный потенциал), Гельмгольца энергия  (изохорно-изотермический потенциал), Гиббса энергия
(изохорно-изотермический потенциал), Гиббса энергия  (изобарно-изотермический потенциал). Все термодинамические потенциалы связаны между собой соотношениями:
(изобарно-изотермический потенциал). Все термодинамические потенциалы связаны между собой соотношениями: 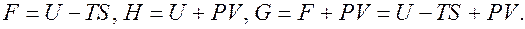 Зная термодинамические потенциалы как функции указанных параметров, по любому из них с помощью дифференцирования по его параметрам можно найти все остальные параметры, характеризующие систему:
Зная термодинамические потенциалы как функции указанных параметров, по любому из них с помощью дифференцирования по его параметрам можно найти все остальные параметры, характеризующие систему: ;
;
 - отношение скорости
- отношение скорости  потока в данной точке к критической скорости
потока в данной точке к критической скорости  :
:  . Приведенная скорость связана с числом Маха
. Приведенная скорость связана с числом Маха  и относительной скоростью
и относительной скоростью  соотношениями
соотношениями
 – показатель адиабаты.
– показатель адиабаты. жидкости пропорционален перепаду давления
жидкости пропорционален перепаду давления  на единицу длины трубки:
на единицу длины трубки: 
 , где
, где  – диаметр трубки,
– диаметр трубки,  – расстояние между этими сечениями,
– расстояние между этими сечениями,  – коэффициент динамической вязкости. Применим только при ламинарном течении жидкости при условии, что длина трубки превышает длину начального участка, необходимого для развития ламинарного течения в трубке (см. Ламинарное течение в круглых трубах, Формула Пуазейля).
– коэффициент динамической вязкости. Применим только при ламинарном течении жидкости при условии, что длина трубки превышает длину начального участка, необходимого для развития ламинарного течения в трубке (см. Ламинарное течение в круглых трубах, Формула Пуазейля). где
где  – давление,
– давление,  – изменение объёма газа. При расширении газа от объёма
– изменение объёма газа. При расширении газа от объёма  до объёма
до объёма  работа газа равна
работа газа равна  Результат интегрирования эависит от характера процесса расширения. При изобарном процессе работа газа при расширении от объёма
Результат интегрирования эависит от характера процесса расширения. При изобарном процессе работа газа при расширении от объёма 



