
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ламинарное течение в круглых трубах.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
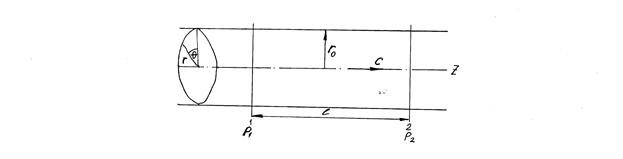
Рассмотрим стационарное ламинарное течение вязкой несжимаемой жидкости в круглой трубе, расположенной горизонтально. Линии тока в этом случае будут представлять собой прямые, параллельные оси трубы. Выберем цилиндрическую систему координат, направив ось Z вдоль оси трубы (Рис.1).
Рис. 1. Из соображений симметрии следует, что
Запишем уравнение неразрывности в цилиндрической системе координат
C учетом (1) уравнение (2) принимает вид
Следовательно
Так как поток осесимметричен, то
Пренебрегая действием массовых сил, запишем уравнение Навье-Стокса в проекциях на координатные оси (в цилиндрической системе координат):
Из уравнений (7) и (8) следует, что давление в сечении постоянно и не зависит от r и p=p(z). (9) Уравнение (6) запишем в виде
Так как c=c(r), p=p(z), то от частных производных перейдем к обычным и уравнение (10) приведем к следующему виду
Дважды проинтегрировав это уравнение, получим
Константу С 1 следует положить равной нулю, т.к. если С 1 ≠ 0, при r→ 0скорость c→ Константу С 2 найдем из условия прилипания вязкой жидкости к стенке трубы, т.е. при r = r 0 (где r 0 – радиус трубы) скорость c(r 0 ) = 0:
Закон распределения скорости по сечению принимает вид
Скорость жидкости на оси трубы при r = 0
Из (14) и (15) следует
т.е. скорость по сечению меняется по параболическому закону. Подсчитаем объемный расход жидкости через поперечное сечение трубы:
При переходе к одномерному потоку
Сравнивая (17) и (18), получим
Подставим (15) в (19)
Из (20)
Отсюда
Интегрируя (22) вдоль оси трубы от сечения 1 до сечения 2, расстояние между которыми
Заменим радиус трубы на диаметр:
Потери на трение по длине трубы между сечениями 1 и 2:
Сравнивая (25) с формулой Дарси-Вейсбаха, получим для коэффициента гидравлического трения
где
что согласуется с опытами Никурадзе для зоны ламинарного течения. Можно показать, что для ламинарного течения коэффициент кинетической энергии Отметим, что ламинарное течение в круглой трубе вихревое. Вихревые линии представляют собой окружности, центры которых лежат на оси трубы. Приведенная выше теория ламинарного течения в круглой трубе хорошо подтверждается опытом за исключением следующих случаев: - При течении с теплообменом. - При течении с большими перепадами давлений – десятки мегапаскалей. Сказывается зависимость вязкости от давления. - При течении в капиллярах и зазорах с облитерацией. В этом случае уменьшается площадь поперечного сечения канала из-за адсорбции полярно-активных молекул на стенках. При постоянном перепаде давлений расход жидкости через капилляр уменьшается. - При течении на начальном участке трубы, где происходит постепенное формирование параболического профиля скоростей. При плавном входе жидкости в трубу из резервуара на начальном участке трубы устанавливается практически равномерное распределение скорости по сечению (Рис. 3). По мере движения жидкости по трубе тормозящее влияние вязкости постепенно распространяется к оси трубы на все большую толщину потока. На входном участке поток имеет ядро, в котором скорость распределена равномерно, и пристенный пограничный слой. Рис. 3. Формирование профиля скоростей на начальном участке трубы Постепенно при движении жидкости пограничный слой растет, а ядро убывает. В конце начального участка формируется параболическое распределение скорости по сечению. Длина начального участка определяется по формуле
где Предполагая, что потери на трение на начальном участке определяются формулой Пуазейля, для падения давления получим
При Лапласа уравнение – см. Уравнение Лапласа. Линия отмеченных частиц – линия, на которой в данный момент времени расположены частицы, прошедшие в разные моменты времени через одну и ту же точку пространства. При установившемся движении линии отмеченных частиц совпадают с траекториями и линиями тока. Линия тока - линия, в каждой точке которой касательная к ней совпадает по направлению со скоростью частицы жидкости в данный момент времени. Совокупность линий тока позволяет наглядно представить в данный момент времени картину течения. В установившемся течении линии тока совпадают с траекториями. Уравнение линии тока
где u, v, w – проекции вектора скорости на оси координат. Лобовое сопротивление (то же, что аэродинамическое сопротивление) — это сила, препятствующая движению тел в жидкостях и газах. Лобовое сопротивления складывается из двух типов сил: сил касательного (тангенциального) трения, направленных вдоль поверхности тела, и сил давления, направленных по нормали к поверхности. Сила сопротивления является диссипативной силой и всегда направлена против вектора скорости тела в среде. Наряду с подъёмной силой является составляющей полной аэродинамической силы.Лобовое сопротивление является результатом необратимого перехода части кинетической энергии тела в теплоту. Лобовое сопротивление М
Магнитная гидродинамика – наука о движении электропроводящих жидкостей и газов в присутствии магнитных полей. Магнуса эффект – см. Эффект Магнуса. Максвелла распределение – закон распределения молекул по скоростям: описывает стационарное распределение частиц (молекул) макроскопической системы, находящейся в термодинамическом равновесии, в отсутствии внешних полей при условии, что движение частиц подчиняется законам классической механики. Функция распределения Употребляется также другая форма распределения Максвелла – распределение молекул по кинетическим энергиям Е. Число молекул
Максимальная скорость
где
где Манометр - прибор, предназначенный для измерения давления или разности давлений жидкостей и газов. Действие манометра основано на зависимости ряда физических параметров от давления. Масса присоединённая – фиктивная масса, которая присоединяется к массе движущегося в жидкости тела для количественной характеристики инерции окружающей его жидкой среды. При неустановившемся поступательном движении тела в идеальной жидкости возникает сопротивление жидкости, пропорциональное ускорению движения тела и обусловленное увлечением среды, окружающей тело; коэффициент пропорциональности и представляет собой присоединённую массу. Физический смысл присоединённоё массы заключается в том, что если присоединить к телу, движущемуся в жидкости, дополнительную массу, равную массе жидкости, увлекаемой телом, то закон его движения в жидкости будет таким же, как в пустоте. Значение присоединённой массы для тел разной формы различно и зависит от ориентации тела относительно направления движения. Массовая сила – см. Объёмная сила. Маха число – см. Число Маха. Метацентр – точка пересечения линии действия выталкивающей силы, проходящей через центр водоизмещения, и продольной плоскости (оси) симметрии тела. От положения метацентра зависит устойчивость равновесия (остойчивость) плавающего тела (судна). При наклонах судна положение метацентра меняется. Плавающее тело (судно) будет остойчивым, если самый низший из его метацентров лежит выше центра тяжести судна. Метацентрическая высота – возвышение метацентра над центром тяжести плавающего тела, служит мерой остойчивости судна. Механика жидкости и газа – то же, что и гидроаэромеханика; раздел механики сплошных сред, в котором изучаются равновесие и движение жидких и газообразных сред, из взаимодействие между собой и с твердыми телами. Механика сплошной среды - раздел механики, изучающий движение и равновесие газов, жидкостей, плазмы и деформируемых твердых тел. В механике сплошных сред вещество рассматривают как непрерывную, сплошную среду, пренебрегая его молекулярным (атомным) строением, и считают непрерывным распределение в среде всех ее характеристик: плотности, напряжений, скоростей частиц и др. Механика сплошных сред подразделяется на гидроаэромеханику, газовую динамику, теорию упругости, теорию пластичности и другие разделы. Механическая энергия - энергия механического движения и взаимодействия тел системы или их частей. Механическая энергия равна сумме кинетической и потенциальной энергии механической системы. Миделевое сечение (мидель) – для движущегося в воде или воздухе тела наибольшее по площади сечение этого тела плоскостью, перпендикулярной направлению движения. К площади миделевого сечения обычно относят действующую на тело силу сопротивления. Миллиметр водяного столба – внесистемная единица давления. 1 мм вод. ст. = 9,80665 Па = 7,355∙10-2 мм ртутного столба. Миллиметр ртутного столба - внесистемная единица давления. 1 мм рт.ст.= 133.322 Па = 13,595 мм водяного столба. Многофазное течение – течение смеси, в которой могут присутствовать газообразная, жидкая и твёрдая фазы нескольких веществ. Многофазное течение, как правило, является неравновесным течением. К многофазным течениям относят течение смеси газа с каплями и твёрдыми частицами одного или нескольких веществ, смеси жидкости с твёрдыми частицами и газовыми пузырями, смеси жидкостей с каплями жидкости и газовыми пузырями другого состава, смеси жидкостей, газов и твёрдых частиц. Многофазное течение – течение гетерогенных смесей. При многофазном течении происходит чрезвычайно сложное взаимодействие фаз, сопровождающееся различными физико-химическими процессами, изменяющими состав, газодинамические и термодинамические параметры каждой из фаз, их массовую долю и размеры включений (жидких либо твёрдых частиц, пузырьков). Моделирование – экспериментальный метод научного исследования, состоящий в замене изучаемого физического (гидромеханического) процесса, явления или объекта другим, ему подобным – моделью. Геометрически подобная оригиналу модель имеет уменьшенный или увеличенный по сравнению с оригиналом размер, а модель процесса или явления может отличаться от реального процесса количественными физическими характеристиками. В основе моделирования лежат теория подобия и анализ размерностей, устанавливающие критерии подобия, равенство которых для натуры и модели обеспечивает возможность переноса экспериментальных результатов, полученных путем физического моделирования, на натурные условия. При равенстве критериев подобия значения переменных величин, характеризующих реальное явление (натуру), пропорциональны в сходственных точках пространства и в сходственные моменты времени значениям тех же величин для модели. Это позволяет производить пересчёт экспериментальных результатов, полученных на модели, на натуру путём умножения каждой из определяемых величин на постоянный для всех величин данной размерности множитель – коэффициент подобия (масштаб моделирования). Поскольку физические величины связаны между собой определенными соотношениями, вытекающими из законов и уравнений физики (гидромеханики), то для данного физического явления можно составить некоторые безразмерные комбинации величин, характеризующих это явление, которые для натуры и модели имеют одно и то же значение. Эти безразмерные комбинации физических величин называются критериями подобия. Равенство критериев подобия для модели и натуры является необходимым условием моделирования. Однако добиться этого равенства удается не всегда, так как не всегда одновременно удовлетворяются все критерии подобия. В механике жидкости и газа основными критериями подобия являются: критерий (число) Рейнольдса Re, критерий (число) Маха M, критерий (число) Фруда Fr, критерий (число) Эйлера Eu, а для нестационарных течений еще и критерий (число) Струхаля Sh. При моделировании гидромеханических процессов необходимо обеспечить равенство соответствующих критериев подобия у модели и натуры. Однако когда при моделировании необходимо обеспечить равенство нескольких критериев подобия, возникают значительные трудности, часто непреодолимые. Поэтому на практике нередко прибегают к приближенному моделированию, при котором часть процессов, играющих второстепенную роль, или вообще не моделируются, или моделируются приближен-но, т. е. моделирование осуществляется по определяющим критериям подобия. Например, при моделировании установившихся течений вязкого сжимаемого газа необходимо обеспечить равенство критериев Re и M и безразмерного числа k, представляющего собой отношение удельных теплоемкостей газа при постоянном давлении и постоянном объеме. В общем случае это сделать невозможно. Поэтому, как правило, обеспечивают для модели и натуры лишь равенство числа Маха М, а влияние на определяемые параметры чисел Re и k исследуют отдельно. – (См. Критерии подобия, Теория подобия). Молекулярно-кинетическая теория газов - рассматривает газ как совокупность слабо взаимодействующих частиц, находящихся в непрерывном хаотическом (тепловом) движении, интенсивность которого зависит от температуры. Молекулы в газах движутся почти свободно в промежутках между столкновениями, приводящими к резкому изменению их скорости. Наблюдаемые физические характеристики газа представляют собой результат усреднённого движения всех его молекул. Для вычисления этих характеристик нужно знать распределение молекул газа по скоростям и пространственным координатам. Определение явного вида функций распределения – основная задача кинетической теории газов. – (См. Больцмана распределение, Максвелла распределение). Н Навье – Стокса уравнения – см. Уравнения Навье – Стокса. Напор – линейная величина, выражающая удельную (отнесенную к единице веса) механическую энергию потока жидкости в данной точке. Различают: - Полный или гидродинамический напор, выражающий полную удельную энергию потока. Определяется уравнением Бернулли – Hгд = z + p/ρg + αc2/2g, где z – высота рассматриваемой точки потока над плоскостью отсчета, p – давление жидкости, ρ – плотность жидкости, g – ускорение силы тяжести, α – коэффициент кинетической энергии (коэффициент Кориолиса), c – скорость жидкости. - Гидростатический или пьезометрический напор: Hп = z + p/ρg - представляет собой сумму удельных потенциальных энергий положения (в поле силы тяжести) и давления. - Скоростной напор: Hc = αc2/2g – представляет собой удельную кинетическую энергию жидкости. Насыщенный пар – пар, находящийся в термодинамическом равновесии с конденсированной фазой (жидкостью, твёрдым телом). Неньютоновская жидкость – вязкая жидкость, коэффициент вязкости которой зависит от приложенных касательных напряжений (от градиента скорости). Для неньютоновской жидкости зависимость между тензорами напряжений и скоростей деформаций является нелинейной. Свойствами неньютоновских жидкостей обладают структурированные дисперсные системы (суспензии, эмульсии), растворы и расплавы некоторых полимеров, течения грязи, шламов и др. Течения таких жидкостей изучает реология. Необратимые процессы – физические процессы, которые могут самопроизвольно протекать только в одном определенном направлении. К ним относятся: диффузия, теплопроводность, внутреннее трение и др., при которых происходит направленный пространственный перенос вещества (диффузия), энергии в форме теплоты (теплопроводность), импульса (внутреннее трение). Неравновесное состояние термодинамической системы - состояние термодинамической системы, в котором хотя бы один из параметров не имеет определенного значения при неизменных внешних воздействиях. Состояние неравновесия характеризуется неоднородностью распределения температуры, давления, плотности, концентраций компонентов или других макроскопических параметров в отсутствие внешних полей или вращения системы как целого. Неравновесное течение – течение гомогенной или гетерогенной смеси, в которой происходят неравновесные физико-химические процессы. Неразрывности уравнение – см. Уравнение неразрывности. Нернста теорема – см. Теорема Нернста. Нестационарное течение – течение жидкости или газа, которое характеризуется переменностью во времени полей скорости и давления. Нормальная (или физическая) атмосфера - внесистемная единица давления, равная давлению столба ртути 760 мм при 0° C, плотности ртути 13595.1 кг/м3 и нормальном ускорении свободного падения. 1 атм = 101325 Па =10332 мм вод. ст. Нормальные условия – физические условия, определяемые давлением Ньютоновская жидкость – вязкая жидкость, подчиняющаяся закону вязкого трения Ньютона. Для прямолинейного ламинарного течения этот закон устанавливает наличие линейной зависимости между касательным напряжением О Обобщенный закон Ньютона – закон, устанавливающий линейную зависимость между тензорами напряжений и скоростей деформаций:
где Эти утверждения представляют собой гипотезу, которая не может быть строго доказана. Но она косвенно подтверждается всей практикой гидромеханики. Для несжимаемой жидкости
Жидкости, удовлетворяющие обобщенному закону Ньютона, называются ньютоновскими. Обратимый процесс в термодинамике – процесс перехода термодинамической системы из одного состояния в другое, который может протекать как в прямом, так и в обратном направлении через те же промежуточные состояния. Обратимый процесс должен протекать столь медленно, чтобы его можно было рассматривать как непрерывный ряд равновесных состояний. Объемная (массовая) сила – сила, действующая на все частицы (элементарные объемы) данного тела и пропорциональная массе частицы. К объемным силам относятся силы тяжести, инерции и др. Для характеристик объемных сил вводится понятие плотности распределения (напряжения). Напряжением объемной силы в точке А называется вектор
где Околозвуковые течения – течение газа в области, в которой скорость потока Оператор Гамильтона (оператор набла) – векторный дифференциальный оператор, символический вектор набла
При векторном умножении вектора
Оператор Лапласа – дифференциальный оператор
ставящий в соответствие функции Оператор Лапласа эквивалентен последовательному взятию операций градиента и дивиргенции: Основная теорема кинематики жидкости (1-я теорема Гельмгольца): Любое движение элементарного объема жидкости в данный момент времени можно представить как результат сложения двух движений: квазитвердого, состоящего из поступательного движения вместе с выбранным полюсом и вращательного вокруг мгновенной оси, проходящей через этот полюс, и деформационного движения:
где
где
Тензор скоростей деформаций жидкой частицы - симметричный тензор 2-го ранга – представим в виде матрицы:
где
- скорости угловых деформаций жидкой частицы в соответствующих координатных плоскостях. С учетом этого, проекции на оси координат деформационной составляющей мгновенной скорости равны:
Основная формула гидростатики: давление в любой точке покоящейся жидкости равно внешнему давлению, сложенному с весовым давлением, т.е. с весом столба жидкости высотой от свободной поверхности до данной точки и площадью основания, равной единице:
где Остойчивость – способность плавающего тела (судна), выведенного из положения равновесия, возвращаться вновь к исходному положению после прекращения действия возмущающих сил. Остойчивость судна зависит от взаимного расположения по высоте корпуса судна его центра тяжести и метацентра. Открытая термодинамическая система - термодинамическая система, которая обменивается веществом и энергией с другими системами. Относительная скорость
где | ||
|
| Поделиться: |

 =
=  ;
; 
 . (1)
. (1) . (2)
. (2)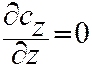 . (3)
. (3) . (4)
. (4) (5)
(5) (6)
(6) (7)
(7) (8)
(8) , т.е.
, т.е. . (10)
. (10) . (11)
. (11) (12)
(12) .
. . (13)
. (13) . (14)
. (14) (15)
(15) , (16)
, (16) (17)
(17) (18)
(18) (19)
(19) (20)
(20) (21)
(21) (22)
(22) , получим формулу Пуазейля
, получим формулу Пуазейля (23)
(23) (24)
(24) (25)
(25) (26)
(26) (27)
(27) (28)
(28)
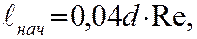 (29)
(29) определяется по формуле (27).
определяется по формуле (27). (30)
(30) любое внешнее возмущение, вносимое в поток с течением времени затухает, поток сохраняет ламинарный характер. При
любое внешнее возмущение, вносимое в поток с течением времени затухает, поток сохраняет ламинарный характер. При 
 зависит от формы и размеров тела, его ориентации относительно направления скорости потока, свойств и состояния среды, в которой происходит движение тела, что учитывается безразмерным коэффициентом лобового сопротивления
зависит от формы и размеров тела, его ориентации относительно направления скорости потока, свойств и состояния среды, в которой происходит движение тела, что учитывается безразмерным коэффициентом лобового сопротивления 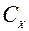 , определяемым экспериментально:
, определяемым экспериментально:  где
где  – плотность среды,
– плотность среды,  – скорость движения тела,
– скорость движения тела,  – наибольшее поперечное сечение тела. В реальных средах на величину лобового сопротивления влияет вязкое трение в пограничном слое между поверхностью тела и средой, потери на вихреобразование и образование ударных волн при около- и сверхзвуковых скоростях движения.
– наибольшее поперечное сечение тела. В реальных средах на величину лобового сопротивления влияет вязкое трение в пограничном слое между поверхностью тела и средой, потери на вихреобразование и образование ударных волн при около- и сверхзвуковых скоростях движения. Максвелла определяет относительное число молекул
Максвелла определяет относительное число молекул  скорости которых лежат в интервале от
скорости которых лежат в интервале от  до
до  и имеет вид:
и имеет вид:  , где
, где 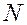 – число молекул,
– число молекул,  – масса молекулы,
– масса молекулы, 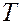 – абсолютная температура,
– абсолютная температура,  – постоянная Больцмана. Число молекул
– постоянная Больцмана. Число молекул  скорости которых лежат в интервале от
скорости которых лежат в интервале от  При помощи функции распределения молекул по скоростям можно вычислить наиболее вероятную скорость
При помощи функции распределения молекул по скоростям можно вычислить наиболее вероятную скорость  (соответствует максимуму функции распределения), а также среднее значение любой функции от скорости молекул: среднюю квадратичную скорость
(соответствует максимуму функции распределения), а также среднее значение любой функции от скорости молекул: среднюю квадратичную скорость  среднюю арифметическую скорость
среднюю арифметическую скорость  .
. Е
Е  , кинетическая энергия которых заключена в интервале от Е до Е
, кинетическая энергия которых заключена в интервале от Е до Е  Е равно
Е равно  Е
Е  Е, где
Е, где  Е
Е  Е
Е  ∙ Е
∙ Е  .
. 
 – скорость, которая достигается при истечении газа в пустоту, когда полная энтальпия газа целиком преобразуется в кинетическую энергию. Из уравнения энергии следует:
– скорость, которая достигается при истечении газа в пустоту, когда полная энтальпия газа целиком преобразуется в кинетическую энергию. Из уравнения энергии следует:
 и
и  – энтальпия и полная энтальпия газа,
– энтальпия и полная энтальпия газа, 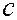 – скорость газа,
– скорость газа,  и
и  температура и полная температура (температура торможения),
температура и полная температура (температура торможения),  – теплоёмкость газа при постоянном давлении,
– теплоёмкость газа при постоянном давлении,  – газовая постоянная,
– газовая постоянная,  – показатель адиабаты. Отсюда следует:
– показатель адиабаты. Отсюда следует: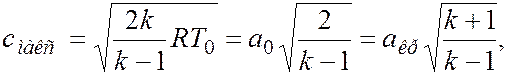
 – скорость звука в заторможенном потоке,
– скорость звука в заторможенном потоке,  – критическая скорость. Максимальная скорость в
– критическая скорость. Максимальная скорость в 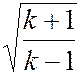 раз превышает критическую скорость.
раз превышает критическую скорость. 101 325 Па (760 мм рт. ст., нормальная атмосфера) и температурой
101 325 Па (760 мм рт. ст., нормальная атмосфера) и температурой  273,15 К (0˚ С).
273,15 К (0˚ С). в плоскостях соприкосновения слоев жидкости и производной от скорости течения
в плоскостях соприкосновения слоев жидкости и производной от скорости течения  по нормали к этим плоскостям, т.е.
по нормали к этим плоскостям, т.е.  где
где  - динамический коэффициент вязкости. В общем случае пространственного течения для ньютоновской жидкости имеет место линейная зависимость между тензорами напряжений и скоростей деформаций. Свойствами ньютоновской жидкости обладает большинство жидкостей (вода, смазочное масло и др.) и все газы.
- динамический коэффициент вязкости. В общем случае пространственного течения для ньютоновской жидкости имеет место линейная зависимость между тензорами напряжений и скоростей деформаций. Свойствами ньютоновской жидкости обладает большинство жидкостей (вода, смазочное масло и др.) и все газы.





 – давление;
– давление;  – нормальные напряжения, а
– нормальные напряжения, а  – касательные;
– касательные;  – проекции скорости на оси координат;
– проекции скорости на оси координат; 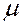 – коэффициент динамической вязкости.
– коэффициент динамической вязкости. и уравнения для нормальных напряжений принимают вид:
и уравнения для нормальных напряжений принимают вид:


 , определяемый условием:
, определяемый условием: ,
, - объемная сила, действующая на элементарный объем
- объемная сила, действующая на элементарный объем  , стягивающийся в точку А. Для силы тяжести напряжение равно ускорению свободного падения
, стягивающийся в точку А. Для силы тяжести напряжение равно ускорению свободного падения  для инерционных сил –
для инерционных сил –  где
где  - плотность жидкости,
- плотность жидкости,  - ускорение.
- ускорение.  мало отличается от местной скорости распространения звука (
мало отличается от местной скорости распространения звука ( ). Околозвуковое течение может быть дозвуковым, сверхзвуковым и смешанным (трансзвуковым), когда внутри рассматриваемой области совершается переход от дозвукового к сверхзвуковому течению. Характерными случаями околозвуковых течений являются течения в области критического (наиболее узкого) сечения сопел ракетных двигателей и аэродинамических труб, вблизи горловины сверхзвуковых воздухозаборников реактивных двигателей, в межлопаточных каналах некоторых турбомашин, обтекание тел, летящих со скоростью, близкой к скорости звука и др.
). Околозвуковое течение может быть дозвуковым, сверхзвуковым и смешанным (трансзвуковым), когда внутри рассматриваемой области совершается переход от дозвукового к сверхзвуковому течению. Характерными случаями околозвуковых течений являются течения в области критического (наиболее узкого) сечения сопел ракетных двигателей и аэродинамических труб, вблизи горловины сверхзвуковых воздухозаборников реактивных двигателей, в межлопаточных каналах некоторых турбомашин, обтекание тел, летящих со скоростью, близкой к скорости звука и др. где
где 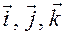 – единичные векторы, направленные вдоль осей координат
– единичные векторы, направленные вдоль осей координат  Вектор набла приобретает смысл в сочетании со скалярной
Вектор набла приобретает смысл в сочетании со скалярной  или векторной
или векторной  функцией, к которой он применяется. В результате умножения вектора
функцией, к которой он применяется. В результате умножения вектора 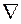 на скалярную функцию
на скалярную функцию  При скалярном умножении вектора
При скалярном умножении вектора  :
:
 Произведение
Произведение  представляет собой дифференциальный оператор Лапласа
представляет собой дифференциальный оператор Лапласа

 функцию
функцию 

 ,
, - скорость жидкой частицы,
- скорость жидкой частицы,  - составляющая скорости в квазитвердом движении,
- составляющая скорости в квазитвердом движении, 

 - скорость поступательного движения;
- скорость поступательного движения;  - угловая скорость вращательного движения вокруг мгновенной оси, проходящей через полюс;
- угловая скорость вращательного движения вокруг мгновенной оси, проходящей через полюс;  - расстояние между полюсом и выбранной точкой частицы. Угловая скорость
- расстояние между полюсом и выбранной точкой частицы. Угловая скорость  С учетом этого, проекции на оси координат составляющей мгновенной скорости в квазитвердом движении равны:
С учетом этого, проекции на оси координат составляющей мгновенной скорости в квазитвердом движении равны:

 Деформационную составляющую скорости можно представить в виде произведения
Деформационную составляющую скорости можно представить в виде произведения  где
где  - тензор скоростей деформаций жидкой частицы.
- тензор скоростей деформаций жидкой частицы. ,
, - скорости относительных линейных деформаций жидких отрезков в направлении соответствующих координатных осей;
- скорости относительных линейных деформаций жидких отрезков в направлении соответствующих координатных осей;
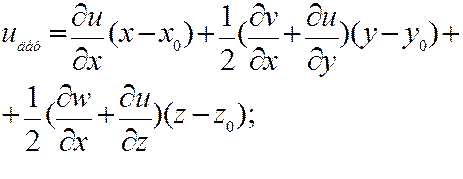

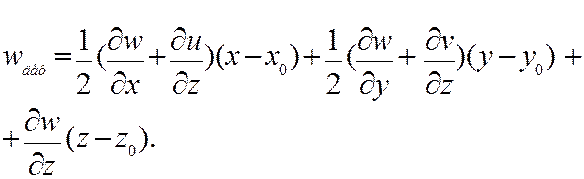

 - давление в данной точке;
- давление в данной точке;  - давление на свободной поверхности;
- давление на свободной поверхности; 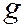 - ускорение свободного падения;
- ускорение свободного падения;  - глубина, на которой находится точка.
- глубина, на которой находится точка. - отношение местной скорости
- отношение местной скорости  макс. Относительная скорость
макс. Относительная скорость  и приведенной скоростью
и приведенной скоростью  следующими соотношениями:
следующими соотношениями:



