
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение атмосферного давления по земной поверхности обусловливает движение воздушных масс и атмосферных фронтов, определяет направление и скорость ветра.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Аэродинамика - раздел гидроаэромеханики, изучающий законы движения газообразной среды и ее силового взаимодействия с движущимися в ней твердыми телами. Основными задачами аэродинамики являются: определение сил, действующих на обтекаемое газом тело; распределение давления на поверхность тела; распределение скоростей в газе, обтекающем тело. Аэродинамическая сила - сила, характеризующая воздействие газообразной среды на движущееся в ней тело. Силовое воздействие среды на тело сводится к силам давления и трения, распределенным по поверхности тела. Такая пространственная система сил может быть приведена к равнодействующей этих сил, называемой аэродинамической силой. В прямоугольной системе координат, связанной с вектором скорости тела, аэродинамическая сила раскладывается на следующие составляющие: аэродинамическое сопротивление, направленное по оси потока в сторону, противоположную направлению движения тела; подъемную силу, перпендикулярную к ней и лежащую в вертикальной плоскости; боковую силу, перпендикулярную аэродинамическому сопротивлению и подъемной силе. Аэродинамическая труба – установка, создающая поток газа (воздуха) с целью изучения воздействия его на обтекаемый объект (самолет, ракету, автомобиль и др.), а также экспериментального исследования аэродинамических явлений. Принцип обратимости движения, согласно которому перемещение тела в неподвижном воздухе может быть заменено движением воздуха относительно неподвижного тела, при соблюдении условий теории подобия позволяет получить значения силовых и тепловых нагрузок, действующих на летательный аппарат, испытывая его модель в аэродинамической трубе. Различают дозвуковые, трансзвуковые и сверхзвуковые аэродинамические трубы. Аэродинамический нагрев – нагрев тел, движущихся с большой скоростью в воздухе или другом газе. Аэродинамический нагрев связан с аэродинамическим сопротивлением, которое испытывают тела при полёте в атмосфере. Энергия, затрачиваемая телом на преодоление сопротивления, частично передаётся телу в виде аэродинамического нагрева. Аэродинамический след – область подторможенной жидкости (газа), возникающая за обтекаемым телом и существующая на некотором протяжении. Аэродинамическое сопротивление (лобовое сопротивление) - составляющая полной аэродинамической силы, характеризующая действие газа на движущееся в нем твердое тело и направленная в сторону, противоположную направлению скорости. Возникает вследствие необратимого перехода кинетической энергии тела в тепловую. Является одной из важнейших характеристик летательного аппарата, определяющих его лётно-технические данные, в частности требуемую тягу двигательной установки. Аэродинамическое сопротивление В идеальной несжимаемой жидкости вихреобразование и образование ударных волн невозможно, поэтому, теоретически, не возникает и аэродинамическое сопротивление (парадокс Д΄ Аламбера – Эйлера). Аэростатика - раздел гидроаэромеханики, изучающий условия равновесия газов и действие неподвижных газов на погруженные в них твердые тела. Основными задачами аэростатики являются: исследование зависимости давления в атмосфере от высоты; исследование поддерживающей силы, которая действует на плавающие в воздухе тела. Аэроупругость – раздел прикладной механики, в котором изучается взаимодействие упругой системы с потоком газа. Явления аэроупругости встречаются во многих областях техники, в строительном деле при изучении ветровых воздействий на мосты и высотные сооружения, в судостроении и энергомашиностроении. Особенно важное значение исследования аэроупругости приобретают в авиации и ракетной технике. Б Барометрическая формула — зависимость давления
где Для идеального газа, находящегося в изотермическом равновесии (имеющего постоянную температуру T) и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения g одинаково), барометрическая формула имеет следующий вид:
Из барометрической формулы следует, что концентрация молекул n (или плотность газа) убывает с высотой по тому же закону:
где n и n0 – концентрация молекул газа соответственно на высотах h и h= 0. Баротропные процессы – процессы изменения состояния жидкости (газа), в которых плотность Бернулли уравнение – см. Уравнение Бернулли. Био – Савара закон – см. Закон Био – Савара. Бойля-Мариотта закон – один из основных газовых законов, описывает изотермические процессы в газе. Согласно закону Бойля-Мариотта при постоянной температуре T объем данной массы газа V обратно пропорционален его давлению P: PV=const. Установлен в 1662 г. Р.Бойлем, в 1676 г. сформулирован также Э.Мариоттом. Строго выполняется только для идеальных газов. Больцмана постоянная (k) ─ одна из фундаментальных физических констант, равная отношению универсальной газовой постоянной R к постоянной Авогадро NА. Больцмана постоянная k = 1,380662·10 -23 Дж/К. Больцмана распределение – описывает равновесное распределение молекул идеального газа во внешнем потенциальном силовом поле: n = n0exp(-W/kT), где n0 – концентрация молекул там, где потенциальная энергия принимается равной нулю; n – концентрация там, где потенциальная энергия равна W; T – температура; k = 1,38·10-23 Дж/K – постоянная Больцмана. Если газ находится в гравитационном поле, W=m0gh, где m0 ─ масса молекулы газа, g ─ ускорение свободного падения, h ─ высота. Броуновское движение – беспорядочное движение малых частиц, взвешенных в жидкости или газе, происходящее под действием ударов молекул окружающей среды. Причины броуновского движения – тепловое движение молекул среды и отсутствие точной компенсации ударов, испытываемых частицей со стороны окружающих её молекул, т.е. броуновское движение обусловлено флуктуациями давления.
В
Вакуум (от лат.Vacuum – пустота) - состояние газа при давлении ниже атмосферного. Физической характеристикой вакуума является соотношение между длиной свободного пробега молекул газа и характерным размером сосуда, в котором находится газ. В зависимости от соотношения между длиной свободного пробега атомов или молекул Вакуумметр – прибор для измерения давлений газов ниже атмосферного. Ван-дер-Ваальса уравнение – уравнение состояния реального газа. Для произвольной массы газа m уравнение Ван-дер-Ваальса имеет вид: Вейсбаха формула – см. Формула Вейсбаха. Вентури трубка – см. Трубка Вентури (Расходомер Вентури). Вечный двигатель [лат. perpetuum mobile ] второго рода – воображаемое периодически действующее устройство, превращающее в полезную работу все количество теплоты, полученное от нагревателя, без каких-либо иных изменений в окружающей среде (без передачи некоторого количества теплоты холодильнику). Утверждение о невозможности вечного двигателя второго рода – одна из возможных формулировок второго начала термодинамики. Вечный двигатель первого рода – воображаемое устройство, которое может совершать работу неограниченное время, не заимствуя энергии извне; создающее энергию из ничего. Невозможность такого двигателя вытекает из первого начала термодинамики (закона сохранения энергии). Вискозиметр – прибор для определения вязкости жидкостей и газов. Вихревое движение – движение жидкости или газа, при котором их частицы перемещаются не только поступательно, но и вращаются вокруг некоторой мгновенной оси. При вихревом движении rot Мгновенная скорость вращения элементарных объемов (мера завихренности) Векторное поле ротора скорости (вихря) характеризуется следующими геометрическими образами: вихревая линия и вихревая трубка Справедливы следующие теоремы о вихрях: Теорема Гельмгольца: Поток вектора ротора скорости через любое сечение вихревой трубки в данный момент времени одинаков вдоль всей трубки:
Поток вектора вихря является величиной, характерной для вихревой трубки. Его называют интенсивностьюJ вихревой трубки: J = Теорема Стокса: Интенсивность вихревой трубки равна циркуляции вектора скорости по замкнутому контуру, расположенному на поверхности трубки и один раз ее опоясывающему: J= За редким исключением, движение жидкости или газа почти всегда бывает вихревым. Так, вихревым является ламинарное течение в круглой трубе, когда скорость распределяется по параболическому закону, течение в пограничном слое при плавном обтекании тела и в следе за плохо обтекаемым телом. Вихревой характер носит любое турбулентное течение. Если обтекание тела происходит при больших числах Re, завихренность порождается в пограничном слое, а затем сносится в основной поток, где формируются отчетливо видимые вихри, некоторое время эволюционирующие и сохраняющие свою индивидуальность. Например, за плохообтекаемым телом образуется регулярная вихревая дорожка Кармана. Вихреобразование в следе за плохообтекаемым телом определяет основную часть лобового сопротивления тела, а образование вихрей у концов крыльев летательных аппаратов вызывает дополнительное индуктивное сопротивление. Вихревая линия – линия, касательная к которой в каждой точке в данный момент времени направлена по вектору ротора скорости, т.е.
где Вихревая трубка – совокупность вихревых линий, проходящих через замкнутую кривую, не являющуюся вихревой линией. Внутреннее трение – см. Вязкость. Внутренняя энергия тела – энергия физической системы, зависящая от её внутреннего состояния. Внутренняя энергия включает энергию хаотического (теплового) движения всех микрочастиц системы (молекул, атомов, ионов и т.д.) и энергию взаимодействия этих частиц. Кинетическая энергия движения системы как целого и ее потенциальная энергия во внешних силовых полях во внутреннюю энергию не входят. Внутренняя энергия Волновая поверхность – геометрическое место точек среды, в которых в рассматриваемый момент времени фаза волны имеет одно и то же значение. Различным значениям фазы соответствует семейство волновых поверхностей. Волновое сопротивление – аэродинамическое сопротивление, возникающее, когда скорость газа относительно тела превышает скорость распространения в газе слабых (звуковых) возмущений (при сверхзвуковом течении). Волновое сопротивление – результат затраты энергии на образование ударных волн. Диссипация энергии в ударной волне происходит вследствие проявления свойств вязкости и теплопроводности в тонком слое ударной волны, где имеются большие градиенты скорости и температуры. Волновое сопротивление в несколько раз превышает сопротивление, связанное с трением и образованием вихрей, зависит от формы тела, угла атаки и числа Маха. Волновое уравнение – линейное однородное уравнение в частных производных гиперболического типа, описывает распространение волн в среде, имеет вид:
Волновой кризис – изменение характера обтекания летательного аппарата воздушным потоком при приближении скорости полета к скорости звука, сопровождающееся, как правило, ухудшением аэродинамических характеристик аппарата – ростом лобового сопротивления, снижением подъемной силы, появлением вибраций и пр. Волновой фронт – геометрическое место точек среды, до которых доходят колебания в данный момент времени; поверхность, на всех точках которой волна имеет в данный момент времени одинаковую фазу. Распространение волны происходит по нормали к волновому фронту и может рассматриваться как движение волнового фронта. Волновой фронт является границей между возмущённой и невозмущённой областями среды. Волны – процесс распространения колебаний некоторой совокупности физических величин в сплошной среде, периодический во времени и пространстве. Процесс распространения волн описывается волновым уравнением. Второе начало (закон) термодинамики – один из основных законов термодинамики; устанавливает необратимость макроскопических процессов, протекающих с Конечной скоростью: процессы, связанные с теплообменом при конечной разнице температур, с трением, с диффузией, с выделением джоулевой теплоты и другие, протекающие с конечной скоростью, необратимы, т.е. могут самопроизвольно протекать только в одном направлении. Имеет две эквивалентные формулировки: В современной термодинамике второе начало термодинамики формулируется как закон возрастания энтропии: в замкнутой макроскопической системе энтропия при любом реальном процессе либо возрастает, либо остается неизменной (в случае обратимых процессов). Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая невозможность перехода всей внутренней энергии системы в полезную работу. Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов иполучило многочисленные экспериментальные подтверждения. Выталкивающая сила (сила Архимеда) - сила, действующая со стороны жидкости или газа на погруженное в них тело. Линия действия выталкивающей силы, проходит через центр водоизмещения. Вязкость (внутреннее трение) – свойство жидкостей и газов оказывать сопротивление перемещению одной их части относительно другой.Вязкость проявляется при движении одних слоев жидкости (газа) относительно других. В этом случае между слоями возникают силы внутреннего трения, направленные вдоль поверхности соприкасающихся слоев и зависящие от их относительных скоростей. Сила внутреннего трения В соответствии с законом Ньютона касательные напряжения Жидкости, динамическая вязкость которых зависит от физических свойств среды и не зависит от градиента скорости, называются ньютоновскими жидкостями (вода, керосин и др.). Жидкости, динамическая вязкость которых зависит и от градиента скорости называются неньютоновскими (расплавы полимеров, суспензии, коллоидные растворы и др.). Закон Ньютона для касательных напряжений справедлив только для ламинарных течений. В турбулентных потоках к касательным напряжениям, обусловленным вязкостью, добавляются турбулентные касательные напряжения, порожденные пульсациями скорости. Молекулярно-кинетическая теория объясняет вязкость движением и взаимодействием молекул. В газах расстояния между молекулами существенно больше радиуса действия молекулярных сил, поэтому вязкость газов – результат хаотического (теплового) движения молекул – явление переноса. Хаотически движущиеся молекулы переносят импульс направленного движения из одного слоя в другой, в результате чего медленные слои ускоряются, а более быстрые замедляются. В кинетической теории газов коэффициент динамической вязкости (внутреннего трения) вычисляется по формуле μ = В жидкостях, где расстояние между молекулами много меньше, чем в газах, вязкость обусловлена в первую очередь межмолекулярным взаимодействием, ограничивающим подвижность молекул. С повышением температуры вязкость жидкостей резко уменьшается. Г Газ ( от греч. Chaos – хаос ) – агрегатное состояние вещества, в котором его частицы не связаны или весьма слабо связаны между собой силами взаимодействия и движутся почти свободно и хаотически в промежутках между столкновениями, во время которых происходит резкое изменение характера их движения. Время столкновения молекул в газах значительно меньше среднего времени их пробега. В отличие от жидкостей и твердых тел газы не образуют свободной поверхности и равномерно заполняют весь доступный им объем. Газ идеальный – теоретическая модель газа, в которой молекулы рассматриваются как не взаимодействующие друг с другом материальные точки. Газовая динамика – раздел гидроаэромеханики, в котором изучается движение сжимаемых сплошных сред (газа, плазмы) и их взаимодействие с твердыми телами. Газовая постоянная универсальная – фундаментальная физическая константа, численно равна работе расширения одного моля идеального газа при постоянном давлении при нагревании на 1 К. Численное значение универсальной газовой постоянной в единицах СИ: R = 8,31441 Дж/(моль·К). В механике жидкости и газа чаще используется газовая постоянная R´, равная универсальной газовой постоянной, делённой на массу моля газа R´=R/M, где М – масса моля. Измеряется в Дж/кг. Для газов, близких к идеальному, R=Cp – Cv, где Cp и Cv – молярные теплоёмкости газа при постоянных давлении и объёме соответственно. Газодинамические функции (изоэнтропические формулы) – формулы, связывающие параметры газового потока – давление Приведем некоторые изоэнтропические формулы. Функция температуры:
Функция давления:
Функция плотности:
Приведенная плотность тока:
где
Приведенный статический импульс:
где Приведенная плотность потока импульса – отношение плотности потока импульса в произвольном сечении энергетически изолированного потока к его значению в заторможенном потоке, т.е. к давлению торможения: Существуют и другие газодинамические функции. Газоструйные излучатели – генераторы акустических колебаний, источником энергии которых служит высокоскоростная газовая струя. Действие газоструйных излучателей основано на создании в струе пульсирующего режима течения; возникающие при этом периодическ ие сжатия и разрежения газа излучаются в пространство в виде акустических волн. Пульсации потока являются следствием возникновения автоколебаний при взаимодействии струи с твёрдым препятствием в виде резонатора, клина или мембраны. Гармоническая функция – функция, непрерывная со своими втор ы ми производными в области Гей-Люссака закон – утверждает, что при постоянном давлении объем Гельмгольца энергия (свободная энергия, изохорно-изотермический потенциал) Гетерогенная система [от греч. heterogenѐs – разнородный] – термодинамическая система, состоящая из различных по физическим и химическим свойствам частей (фаз), отделенных друг от друга резкими поверхностями раздела. Гиббса энергия (изобарно-изотермический потенциал, свободная энтальпия, термодинамический потенциал Гиббса) Гидравлика - наука о законах движения и равновесия жидкостей и способах приложения этих законов к решениям задач инженерной практики. Гидравлика изучает движение капельных жидкостей, считая их несжимаемыми. В гидравлике не рассматривается молекулярное строение жидкости, считается, что жидкость представляет сплошную, непрерывную среду. Гидравлический радиус – отношение площади Гидравлический удар — явлениерезкого изменения давления в жидкости, вызванное быстрым (мгновенным) изменением скорости ее течения в напорном трубопроводе, возникающее при быстром перекрытии запорных устройств. Теорию гидравлического удара разработал в 1869 г. Н. Е. Жуковский. Увеличение давления при гидравлическом ударе определяется в соответствии с его теорией по формуле: При абсолютно жестких стенках трубопровода скорость распространения ударной волны равна скорости звука в жидкости. В трубах с упругими стенками
где Если скорость v1 = 0, гидравлический удар называется полным, если v1 ≠ 0 – неполным. С момента начала закрытия задвижки в трубе возникает волна повышения давления, которая распространяется по трубе, отражается от входного конца с переменой знака и в виде обратной волны возвращается к задвижке. Время от возникновения волны и до возврата ее к задвижке называется фазой удара:
где | ||
|
| Поделиться: |

 зависит от формы и размеров тела, его ориентации относительно направления скорости потока, свойств и состояния среды, в которой происходит движение тела, что учитывается безразмерным коэффициентом лобового сопротивления
зависит от формы и размеров тела, его ориентации относительно направления скорости потока, свойств и состояния среды, в которой происходит движение тела, что учитывается безразмерным коэффициентом лобового сопротивления 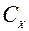 , определяемым экспериментально:
, определяемым экспериментально: 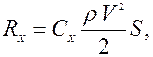 где
где  – плотность среды,
– плотность среды,  – скорость движения тела,
– скорость движения тела,  – наибольшее поперечное сечение тела. В реальных средах на величину лобового сопротивления влияет вязкое трение в пограничном слое между поверхностью тела и средой, потери на вихреобразование и образование ударных волн при около- и сверхзвуковых скоростях движения.
– наибольшее поперечное сечение тела. В реальных средах на величину лобового сопротивления влияет вязкое трение в пограничном слое между поверхностью тела и средой, потери на вихреобразование и образование ударных волн при около- и сверхзвуковых скоростях движения.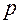 или плотности
или плотности 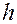 в поле силы тяжести. В случае, если температура
в поле силы тяжести. В случае, если температура  воздуха зависит от высоты –
воздуха зависит от высоты –  , барометрическая формула принимает вид
, барометрическая формула принимает вид
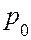 – давление у поверхности Земли (
– давление у поверхности Земли ( ,
, 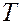 – температура,
– температура,  – ускорение силы тяжести,
– ускорение силы тяжести,  – газовая постоянная.
– газовая постоянная.

 ,
, К баротропным процессам относятся течение несжимаемой жидкости (
К баротропным процессам относятся течение несжимаемой жидкости ( изотермический
изотермический  и адиабатный
и адиабатный 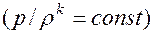 процессы, где
процессы, где  – показатель адиабаты.
– показатель адиабаты.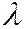 и линейным размером сосуда
и линейным размером сосуда  различают высокий (
различают высокий ( где
где  - число молей газа,
- число молей газа,  – объем,
– объем,  – универсальная газовая постоянная,
– универсальная газовая постоянная, 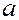 и
и  – постоянные для каждого газа величины, определяемые опытным путем.
– постоянные для каждого газа величины, определяемые опытным путем. ≠ 0 в данной области течения жидкости.
≠ 0 в данной области течения жидкости.  где c – скорость жидкой частицы.
где c – скорость жидкой частицы.


 ||
||  , где
, где  получаем уравнение вихревой линии:
получаем уравнение вихревой линии:
 - проекции вектора угловой скорости на оси координат. При установившемся движении вихревые линии в различные моменты времени совпадают друг с другом.
- проекции вектора угловой скорости на оси координат. При установившемся движении вихревые линии в различные моменты времени совпадают друг с другом. является однозначной функцией состояния системы, т.е.
является однозначной функцией состояния системы, т.е.  или
или  , где
, где  ─ давление,
─ давление, 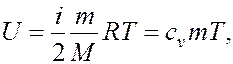 где
где  число степеней свободы молекулы газа,
число степеней свободы молекулы газа,  - масса газа,
- масса газа,  ─ масса моля газа,
─ масса моля газа,  ─ удельная теплоёмкость газа при постоянном объёме. Согласно первому началу термодинамики изменение внутренней энергии системы
─ удельная теплоёмкость газа при постоянном объёме. Согласно первому началу термодинамики изменение внутренней энергии системы  , где
, где  ─ количество теплоты, сообщаемое системе,
─ количество теплоты, сообщаемое системе,  ─ работа, совершаемая системой. Согласно второму началу термодинамики,
─ работа, совершаемая системой. Согласно второму началу термодинамики, 
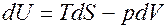 . Внутренняя энергия как функция энтропии и объёма
. Внутренняя энергия как функция энтропии и объёма  является одним из, так как определяет все термодинамические свойства системы.
является одним из, так как определяет все термодинамические свойства системы. где
где 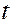 ─ время,
─ время,  ─ пространственные декартовы координаты,
─ пространственные декартовы координаты,  ─ функция, характеризующая возмущение среды в точке с координатами
─ функция, характеризующая возмущение среды в точке с координатами 
 ─ фазовая скорость распространения волны.
─ фазовая скорость распространения волны. между слоями определяется формулой Ньютона
между слоями определяется формулой Ньютона  где
где  – коэффициент динамической вязкости (динамическая вязкость);
– коэффициент динамической вязкости (динамическая вязкость); 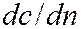 – градиент скорости в направлении, перпендикулярном движению;
– градиент скорости в направлении, перпендикулярном движению;  – площадь соприкасающихся слоев. Сила внутреннего трения ускоряет медленный слой и замедляет быстрый слой. Единица измерения динамической вязкости – Па∙с. Различают также кинематическую вязкость
– площадь соприкасающихся слоев. Сила внутреннего трения ускоряет медленный слой и замедляет быстрый слой. Единица измерения динамической вязкости – Па∙с. Различают также кинематическую вязкость  где
где  – плотность жидкости. Единица измерения кинематической вязкости – м2/с.
– плотность жидкости. Единица измерения кинематической вязкости – м2/с. в движущейся жидкости определяются по формуле:
в движущейся жидкости определяются по формуле: 
 где
где  - средняя скорость теплового движения молекул,
- средняя скорость теплового движения молекул,  - средняя длина свободного пробега молекул. С ростом температуры вязкость газов увеличивается.
- средняя длина свободного пробега молекул. С ростом температуры вязкость газов увеличивается. плотность
плотность 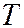 (и некоторые другие характеристики течения) в произвольном сечении с параметрами заторможенного потока
(и некоторые другие характеристики течения) в произвольном сечении с параметрами заторможенного потока 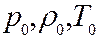 в изоэнтропийном адиабатическом движении газа при помощи безразмерных скоростей
в изоэнтропийном адиабатическом движении газа при помощи безразмерных скоростей  , где
, где  – число Маха – отношение скорости потока
– число Маха – отношение скорости потока  в данном сечении к местной скорости звука
в данном сечении к местной скорости звука 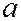 ;
;  – приведенная скорость (скоростной коэффициент, коэффициент скорости) – отношение скорости потока
– приведенная скорость (скоростной коэффициент, коэффициент скорости) – отношение скорости потока  ;
;  – относительная скорость – отношение скорости потока
– относительная скорость – отношение скорости потока  .
.



 .
.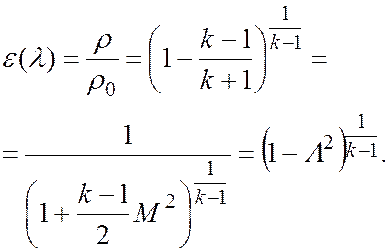

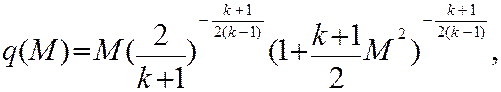
 – критическая плотность,
– критическая плотность,  – площадь сечения, в котором достигается критический режим течения.
– площадь сечения, в котором достигается критический режим течения.


 и удовлетворяющая в
и удовлетворяющая в  где
где  ─ начальный объем газа,
─ начальный объем газа,  =(1/273) ─ коэффициент теплового расширения, одинаков для всех газов. Закон Гей-Люссака для двух состояний газа можно представить также в виде
=(1/273) ─ коэффициент теплового расширения, одинаков для всех газов. Закон Гей-Люссака для двух состояний газа можно представить также в виде  , где
, где  – один из термодинамических потенциалов, характеристическая функция термодинамической системы при выборе в качестве независимых термодинамических переменных объёма
– один из термодинамических потенциалов, характеристическая функция термодинамической системы при выборе в качестве независимых термодинамических переменных объёма  и энтропией
и энтропией  . Изменение свободной энергии при квазистатическом процессе равно
. Изменение свободной энергии при квазистатическом процессе равно 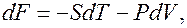 где
где 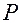 – давление. Поэтому при изотермическом равновесном процессе убыль энергии Гельмгольца равна полной работе, совершаемой системой:
– давление. Поэтому при изотермическом равновесном процессе убыль энергии Гельмгольца равна полной работе, совершаемой системой: 
 Энергия Гиббса связана с энтальпией
Энергия Гиббса связана с энтальпией  соотношением
соотношением 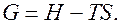 Энергия Гиббса для однокомпонентной системы пропорциональна числу частиц
Энергия Гиббса для однокомпонентной системы пропорциональна числу частиц  в системе:
в системе: 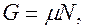 где
где  – химический потенциал, зависящий от
– химический потенциал, зависящий от 
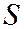 поперечного сечения потока к смоченному периметру
поперечного сечения потока к смоченному периметру  , т.е. к периметру части русла, находящейся под уровнем жидкости:
, т.е. к периметру части русла, находящейся под уровнем жидкости:  Гидравлический радиус служит обобщенной характеристикой размера сечения трубы некруглой формы или открытого русла.
Гидравлический радиус служит обобщенной характеристикой размера сечения трубы некруглой формы или открытого русла.
 где
где  — увеличение давления в Н/м², ρ — плотность жидкости в кг/м³;
— увеличение давления в Н/м², ρ — плотность жидкости в кг/м³;  и
и  — средние скорости в трубопроводе до и после закрытия задвижки (запорного клапана) в м/с;
— средние скорости в трубопроводе до и после закрытия задвижки (запорного клапана) в м/с; 

 - модуль упругости жидкости;
- модуль упругости жидкости;  - модуль упругости материала стенки;
- модуль упругости материала стенки;  и
и 
 - фаза удара,
- фаза удара, 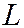 - расстояние от начала трубы до задвижки. В зависимости от фазы удара и времени перекрытия задвижки (или другой запорной арматуры) t, различают два вида ударов:
- расстояние от начала трубы до задвижки. В зависимости от фазы удара и времени перекрытия задвижки (или другой запорной арматуры) t, различают два вида ударов:


